唯一分解定理 （ 内含 求出n的因子个数）

唯一分解定理

一个数n肯定能被分解成  n = 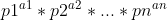. 因为一个数肯定是由合数和质数构成的，合数又可以分解成质数和合数，最后递归下去就会变成质数的乘积。比如36 -> 2*2*3*3 -> .

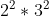最后化成了质数相乘的形式。

(2)中运用等比数列求和公式可化简为：

好，现在给出唯一分解定理的两个小应用

1. 求出数n的因子个数

n =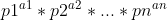

有一个很简洁的公式: n的因子个数 = (1+a1​)(1+a2​)...(1+an​)

因此，我们可以用质因子分解的方法求出一个数的因子个数。

质因子分解

顾名思义，先要找出待分解整数n内的所有质数。然后不断扫描可整除n的质数，发现可整除的就不断除之。直到这个数为1为止。

找到所有质数的方法简单，就是埃拉托斯特尼筛法。见代码：

int primes[1000000] = {2};
bool isnotprime[10000001] = {1, 1, 0, 0, 1, 0, 1, 0};

    int i, j, k = 1;
    for (i = 3; i * i <= n; i += 2) // 偶数肯定不是质数，2除外
    {
        if (!isnotprime[i])
        {
            primes[k++] = i;
            for (j = i; i * j <= n; j += 2)
            {
                isnotprime[i * j] = true;
            }
        }
    }
    for (; i <= n; i += 2) // 把后续的质数取出来
    {
        if (!isnotprime[i]) primes[k++] = i;
    }

然后，不断扫描这些质数，找到整除的就不断除。同时用公式求出因子个数。( 下方代码还可以优化，详见C题 )

    long long fact = 1;
    for (j = 0; n > 1 && j < k; j++) // 如果n变为1则停止分解
    {
        cnt = 0;
        while (n % primes[j] == 0)
        {
            cnt++;
            n /= primes[j];
        }
        fact *= cnt + 1;
    }
    printf("%lld", fact);

但这样太暴力！对不对？

线性算法

埃拉托斯特尼筛法的时间复杂度是O(nlogn)

O(nlogn)，质因子分解的时间复杂度也是O(nlogn)O(nlogn)。当然，这个时间常数非常小，所以并不慢。

但如果是下面这个问题呢？

我们来考察整数1,2,3,...,n

1,2,3,...,n的因子个数之和。如果按照上面质因子分解的方法，求出1~n所有数的因子个数，总的时间复杂度变成O(n2logn)O(n2logn)。当n=106

n=106时，这已经不可接受了。我们必须找到更快的方法。

既然是因子个数，那我们就另辟蹊径，从所有因子而不是质因子的角度考查。

所有数都含有因子1

含有因子2的数：2 4 6 8 10 …

含有因子3的数：3 6 9 12 15 …

含有因子f的数：f 2f 3f …

可得出结论：整数1~n之间，有[n/f]个整数含有因子f，中括号表示向下取整。

这下，这个问题变得非常简单：整数1~n的因子个数之和s(n)

s(n)为：
                                                      s(n) = n + [n/2] + [n/3] + ... + [n/n]

这显然是线性的算法。

回到原问题，如果要求整数n的因子个数，则可以用s(n)−s(n−1)

s(n)−s(n−1)的方法求出。这依然是线性算法。代码如下：

int main()
{
    int n, i, s, t;
    scanf("%d", &n);
    if (n <= 1)
    {
        printf("1");
        exit(0);
    }
    for (i = 1, s = 0; i <= n; i++) s += n / i;
    for (i = 1, t = 0; i < n; i++) t += (n-1) / i;
    printf("%d", s - t);
    return 0;
}

是不是很简单？有时候要有小学生思维！