填空题
-
已知集合 A = { 1 , 2 , 4 } A=\{1,2,4\} A={1,2,4}, B = { 2 , 3 , 4 } B=\{2,3,4\} B={2,3,4},求 A ∩ B = A \cap B= A∩B=______。1
-
lim n → ∞ n + 1 3 n − 1 = \lim\limits _{n\to\infin}\frac{n+1}{3n-1}= n→∞lim3n−1n+1=_____。2
-
已知复数 z = 1 − 2 i ( i z=1-2i(i z=1−2i(i 为虚数单位 ) ) ),则 ∣ z ∣ = | z |= ∣z∣=_____。3
-
已知行列式 ∣ 1 a c 2 d b 3 0 0 ∣ = 6 \begin{vmatrix}1&a&c\\2&d&b\\3&0&0 \end{vmatrix}=6 ∣∣∣∣∣∣123ad0cb0∣∣∣∣∣∣=6,则行列式 ∣ a c d b ∣ = \begin{vmatrix}a&c\\d&b \end{vmatrix}= ∣∣∣∣adcb∣∣∣∣=____。4
-
已知 f ( x ) = x 3 f(x)=x^3 f(x)=x3,则 f − 1 ( x ) = f^{-1}(x)= f−1(x)=____。5
-
已知a、b、1、2的中位数为3,平均数为4,则ab=____。6
-
已知 { x + y ≥ 2 y ≥ 0 x + 2 y − 3 ≤ 0 \begin{cases}x+y\ge2\\y\ge0\\x+2y-3\le0\end{cases} ⎩⎪⎨⎪⎧x+y≥2y≥0x+2y−3≤0,则 z = y − 2 x z=y-2x z=y−2x的最大值为_____7。
-
已知 { a n } \{a_n\} {an}是公差不为零的等差数列,且 a 1 + a 10 = a 9 a_1+a_{10}=a_9 a1+a10=a9,则 a 1 + a 2 + ⋯ a 9 a 10 = \frac{a_1+a_2+\cdots a_9}{a_{10}}= a10a1+a2+⋯a9=_____。8
-
从6个人中挑选4个人去值班,每个人值班1天,第一天需要1人,第二天需要1人,第三天需要2人,则有___9种排法。
-
椭圆 x 2 4 + y 2 3 = 1 \frac{x^2}{4}+\frac{y^2}{3}=1 4x2+3y2=1,过右焦点 F F F作直线 l l l交椭圆于 P P P、 Q Q Q两点 P P P在第二象限,已知 Q ( x Q , y Q ) , Q ′ ( x Q ′ , y Q ′ ) Q(x_{\scriptscriptstyle Q},y_{\scriptscriptstyle Q}),Q'(x'_{\scriptscriptstyle Q},y'_{\scriptscriptstyle Q}) Q(xQ,yQ),Q′(xQ′,yQ′)都在椭圆上,且 y Q + y Q ′ = 0 y_{\scriptscriptstyle Q}+y'_{\scriptscriptstyle Q}=0 yQ+yQ′=0, F Q ⊥ P Q FQ\perp PQ FQ⊥PQ,则直线 l l l的方程为____________10。
-
设 a ∈ R a \in R a∈R,若存在定义域 R R R的函数 f ( x ) f(x) f(x)既满足“对任意 x 0 ∈ R x_0 \in R x0∈R, f ( x 0 ) f(x_0) f(x0)的值为 x 0 2 x^2_0 x02 或 x 0 x_0 x0 ” 又满足 “关于 x x x 的方程 f ( x ) = a f(x)=a f(x)=a 无实数解”,则 a a a 的取值范围为______。11
-
已知 a 1 → , a 2 → , b 1 → , b 2 → , … , b k → ( k ∈ N + ) \overrightarrow {a_1},\overrightarrow {a_2},\overrightarrow {b_1},\overrightarrow {b_2},\dots,\overrightarrow {b_k}(k \in N^+) a1,a2,b1,b2,…,bk(k∈N+) 是平面内凉凉互不平等的向量,满足 ∣ a 1 → − a 2 → ∣ = 1 |\overrightarrow {a_1}-\overrightarrow{a_2}|=1 ∣a1−a2∣=1 且 ∣ a i → − b j → ∣ ∈ { 1 , 2 } ( |\overrightarrow {a_i}-\overrightarrow{b_j}| \in \{1,2\}( ∣ai−bj∣∈{1,2}(其中 i = 1 , 2 , j = 1 , 2 , … , k ) i=1,2,j=1,2,\dots,k) i=1,2,j=1,2,…,k),则 k k k 的最大值为____。12
单选题
-
下列不等式恒成立的是( )。13
A. a 2 + b 2 ≤ 2 a b a^2+b^2 \le 2ab a2+b2≤2ab
B. a 2 + b 2 ≥ − 2 a b a^2+b^2 \ge -2ab a2+b2≥−2ab
C. a 2 + b 2 ≥ − 2 ∣ a b ∣ a^2+b^2 \ge -2\sqrt{|ab|} a2+b2≥−2∣ab∣
D. a 2 + b 2 ≤ 2 ∣ a b ∣ a^2+b^2 \le 2\sqrt{|ab|} a2+b2≤2∣ab∣ -
已知直线 l l l 的解析式为 3 x − 4 y + 1 = 0 3x-4y+1=0 3x−4y+1=0,则下列各式是 l l l 的参数方程的是( )。14
A. { x = 4 + 3 t y = 3 − 4 t \begin{cases}x=4+3t\\y=3-4t\end{cases} {x=4+3ty=3−4t
B. { x = 4 + 3 t y = 3 + 4 t \begin{cases}x=4+3t\\y=3+4t\end{cases} {x=4+3ty=3+4t
C. { x = 1 − 4 t y = 1 + 3 t \begin{cases}x=1-4t\\y=1+3t\end{cases} {x=1−4ty=1+3t
D. { x = 1 + 4 t y = 1 + 3 t \begin{cases}x=1+4t\\y=1+3t\end{cases} {x=1+4ty=1+3t -
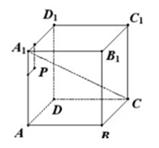
在棱长为 10 10 10的正方体 A B C D — A 1 B 1 C 1 D 1 ABCD\text{---} A_1B_1C_1D_1 ABCD—A1B1C1D1 中, P P P 为左侧面 A D D 1 A 1 ADD_1A_1 ADD1A1 上一点,已知点 P P P到 A 1 D 1 A_1D_1 A1D1的距离为 3 3 3,点P到 A A 1 AA_1 AA1的距离为 2 2 2,则过点 P P P且与 A 1 C A_1C A1C平行的直线交整体于 P P P、 Q Q Q两点,则 Q Q Q点所在的平面是( )。15
A. A A 1 B 1 B AA_1B_1B AA1B1B
B. B B 1 C 1 C BB_1C_1C BB1C1C
C. C C 1 D 1 D CC_1D_1D CC1D1D
D. A B C D ABCD ABCD -
若存在 a ∈ R a \in R a∈R 且 a ≠ 0 a \neq 0 a=0,对任意的 x ∈ R x \in R x∈R,均有 f ( x + a ) < f ( x ) + f ( a ) f(x+a) \lt f(x)+f(a) f(x+a)<f(x)+f(a) 恒成立; 则称函数 f ( x ) f(x) f(x) 具有性质 P P P ,已知 q 1 q_1 q1: f ( x ) f(x) f(x) 单调递减,且 f ( x ) > 0 f(x)\gt 0 f(x)>0 恒成立; q 2 q_2 q2: f ( x ) f(x) f(x) 单调递增,存在 x 0 x_0 x0 使得 f ( x 0 ) = 0 f(x_0)=0 f(x0)=0 ,则是 f ( x ) f(x) f(x) 具有性质 P 的充分条件是( )。 16
A. 只有 q 1 q_1 q1
B. 只有 q 2 q_2 q2
C. q 1 q_1 q1 和 q 2 q_2 q2
D. q 1 q_1 q1和 q 2 q_2 q2都不是
简答题
-
已知边长为 1 1 1 的正方形 A B C D ABCD ABCD ,沿 B C BC BC 旋转有一周得到圆柱体。17
(1)求圆柱体的表面积;
(2)正方形 A B C D ABCD ABCD绕BC逆时针旋转 π 2 \pi \over 2 2π 到 A 1 B C D 1 A_1BCD_1 A1BCD1,求 A D 1 AD_1 AD1 与平面 A B C D ABCD ABCD所成的角。 -
已知 f ( x ) = sin ω x ( ω > 0 ) f(x)=\sin\omega x(\omega\gt0) f(x)=sinωx(ω>0)。
(1) 若 f ( x ) f(x) f(x)的周期是 4 π 4\pi 4π ,求 ω \omega ω,并求此时 f ( x ) = 1 2 f(x)= {1 \over 2} f(x)=21的解集;
(2) 已知 ω = 1 \omega=1 ω=1, g ( x ) = f 2 ( x ) + 3 f ( − x ) f ( π 2 − x ) g(x)=f^2(x)+\sqrt{3}f(-x)f({\pi\over2}-x) g(x)=f2(x)+3f(−x)f(2π−x), x ∈ [ 0 , π 4 ] x\in\left[0,{\pi\over4}\right] x∈[0,4π],求 g ( x ) g(x) g(x)的值域。18 -
已知: v = q x v={q\over x} v=xq, x ∈ ( 0 , 80 ] x\in(0,80] x∈(0,80],且 v = { 100 − 135 ( 1 3 ) 80 x x ∈ ( 0 , 40 ) − k ( x − 40 ) + 85 x ∈ [ 40 , 80 ] ( k > 0 ) v=\begin{cases}100-135({1\over3})^{80\over x}&x\in(0,40)\\-k(x-40)+85&x\in[40,80]\end{cases}(k\gt0) v={100−135(31)x80−k(x−40)+85x∈(0,40)x∈[40,80](k>0),
(1) 若 v > 95 v\gt95 v>95,求x的取值范围;
(2) 已知 x = 80 x=80 x=80, v = 50 v=50 v=50,求 x x x为多少时, q q q可以取得最大值,并求出该最大值。 -
双 曲 线 C 1 : x 2 4 2 − y 2 b 2 = 1 , 圆 C 2 : x 2 + y 2 = 4 + b 2 ( b > 0 ) 在 第 一 象 限 焦 点 为 A , A ( x A , y A ) , 曲 线 Γ = { x 2 4 2 − y 2 b 2 = 1 ∣ x ∣ > x A x 2 + y 2 = 4 + b 2 ∣ x ∣ > x A \def\c{{x^2\over4^2}-{y^2\over b^2}=1}\def\r{x^2+y^2=4+b^2} \def\t#1{\text#1}\t{双曲线} C_1:\c,\t{圆} C_2:\r(b\gt0) \\\t{在第一象限焦点为}A\t,A(x_A,y_A),\\ \t{曲线}\Gamma=\begin{cases}\c&|x|\gt x_A\\\r&|x|\gt x_A\end{cases} 双曲线C1:42x2−b2y2=1,圆C2:x2+y2=4+b2(b>0)在第一象限焦点为A,A(xA,yA),曲线Γ={42x2−b2y2=1x2+y2=4+b2∣x∣>xA∣x∣>xA。
(1) 若 x A = 6 x_A=\sqrt6 xA=6,求 b b b;
(2) 若 b = 5 b=\sqrt5 b=5, C 2 C_2 C2与 x x x轴焦点记为 F 1 F_1 F1、 F 2 F_2 F2, P P P是曲线 Γ \Gamma Γ 上一点,且在第一象限,并满足, ∣ P F 1 ∣ = 8 |PF_1|=8 ∣PF1∣=8,求 ∠ F 1 P F 2 \angle F_1PF_2 ∠F1PF2;
(3) 过点 S ( 0 , 2 + b 2 2 ) S(0,2+{b^2\over2}) S(0,2+2b2) 且斜率为 b 2 b\over2 2b 的直线 l l l 交曲线 Γ \Gamma Γ 于 M M M、 N N N两点,用 b b b 的代数式表示 O M → ⋅ O N → \overrightarrow{OM}\cdot\overrightarrow{ON} OM⋅ON,并求出 O M → ⋅ O N → \overrightarrow{OM}\cdot\overrightarrow{ON} OM⋅ON的取值范围。 -
有限数列 { a n } \{a_n\} {an},若满足 ∣ a 1 − a 2 ∣ ≤ ∣ a 1 − a 3 ∣ ≤ ∣ a 1 − a m ∣ |a_1-a_2|\le|a_1-a_3|\le|a_1-a_m| ∣a1−a2∣≤∣a1−a3∣≤∣a1−am∣, m m m是项数,则称 { a n } \{a_n\} {an}满足性质 P P P。
(1) 判断数列 3 , 2 , 5 , 1 3,2,5,1 3,2,5,1和 4 , 3 , 2 , 5 , 1 4,3,2,5,1 4,3,2,5,1是否具有性质 P P P,请说明理由。
(2) 若 a 1 = 1 a_1=1 a1=1公比为 q q q的等比数列,项数为 10 10 10,具有性质 P P P,求 q q q的取值范围;
(3) 若 a n a_n an是 1 , 2 , … , m 1,2,\dots,m 1,2,…,m是一个排列 ( m ≥ 4 ) , b k = a k + 1 ( k = 1 , 2 , … m − 1 ) , { a n } , { b n } (m\ge4),b_k=a_{k+1}(k=1,2,\dots m-1),\{a_n\},\{b_n\} (m≥4),bk=ak+1(k=1,2,…m−1),{an},{bn}都具有性质 P P P,求室友满足条件的 { a n } \{a_n\} {an}。
{ 2 , 4 } \{2,4\} {2,4} ↩︎
1 3 \frac{1}{3} 31 ↩︎
5 \sqrt{5} 5 ↩︎
2 2 2 ↩︎
x 1 3 ( x ∈ R ) x^{\frac{1}{3}}(x\in R) x31(x∈R) ↩︎
36 36 36 ↩︎
− 1 -1 −1 ↩︎
27 8 \frac{27}{8} 827 ↩︎
180 180 180 ↩︎
x + y − 1 = 0 x+y-1=0 x+y−1=0 ↩︎
( − ∞ , − 0 ) ∪ ( 0 , 1 ) ∪ ( 1 , ∞ ) (-\infin,-0)\cup(0,1)\cup(1,\infin) (−∞,−0)∪(0,1)∪(1,∞) ↩︎
6 6 6 ↩︎
B ↩︎
D ↩︎
D ↩︎
C ↩︎
(1) 4 π 4\pi 4π
(2) arcsin 3 3 \arcsin{ \sqrt3 \over3} arcsin33 ↩︎(1) ω = 1 2 x ∈ { x ∣ x = π 3 + 4 k π 或 x = 5 π 3 + 4 k π , k ∈ Z } \\\omega={1\over2}\\x\in\left\{{x|x={\pi\over3}+4k\pi或x={5\pi\over3}+4k\pi,k\in Z}\right\} ω=21x∈{x∣x=3π+4kπ或x=35π+4kπ,k∈Z}
(2) [ − 1 2 , 0 ] \left[-{1\over2},0\right] [−21,0] ↩︎







 本文包含一系列数学填空题与选择题的解答,涵盖集合论、极限、复数、行列式、函数反演、概率统计、线性代数、几何学等多个数学分支,适合高中及大学数学课程复习。
本文包含一系列数学填空题与选择题的解答,涵盖集合论、极限、复数、行列式、函数反演、概率统计、线性代数、几何学等多个数学分支,适合高中及大学数学课程复习。
















 3740
3740

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








