图的最短路 Bellman-Ford Dijkstra Floyd_Warshall SPFA Johnson 图文分析

强行把自己从小说的诱惑中拉出来写博客。—2019.1.23（下午）

为了能更加准确地表达表达概念，我将会从《挑战程序设计竞赛》中摘取部分内容用于博客描述。此外，以下所有图片均引用自《挑战程序设计竞赛》。

本来想把图的那些内容在一章里写完，但想到这样别人岂不是会搜不到我的理解，亏了，就绝对把算法这几部分单开。（虽然这样还是很可能搜不到）

最短路问题是给定两个顶点，在以这两个点为起点和终点的路径中，求边的权值和最小的的路径。
单源最短路是固定一个起点，求它到其他所有点的最短路问题，终点也固定的问题，叫做两点之间最短路问题，但实际求解方法也一样，因此通常当作单源最短路求解。
记从起点s出发到顶点i的最短距离为d[i]，则下列等式成立：
d[i]=min{d[j]+从j到i的边的权值|（j,i属于E）}。
因此，此类题目开始时设初值d[s]=0，d[i]=INF，在不断用这条递推式更新d的值，只要不含负圈，就可以在有限的操作内求出最小值。

单源最短路问题1（Bellman-Ford算法）

Bellman-Ford算法照我的理解，可以想象成在探路的过程。假设d[i]=INF处为未知地带，d[i]!=INF处为已知地带，每次都从已知的地点向未知处探路一格，更新一次，直至所有路都走通为止。操作思想和dp差不多，不断更新最短数据。

struct edgre{int from,to,cost;}; 
edge infor[MAXN];//结构体数组记录边起点终点和权值
int d[MAXN];//最短距离 
int V,E;//点和边数 
woid shortest_path(int s)
{
    for(int i=1;i<=V;i++)
        d[i]=INF;
    d[s]=0;//初始化 
    while(true)
    {
        bool update=false;
        for(int i=0;i<E;i++)
        {
            edge e=infor[i];
            if(d[e.from]!=INF&&d[e.to]>d[e.from]+e.cost)//从已走过的点向后更新 
            {
                d[e.to]=d[e.from]+e.cost;
                update=true;
            }
        }
        if(!update) break;//起点到所有其他点都已更新为最短时，update不会改为true，结束 
    }
}

每个点每条边都走过一次，时间复杂度为O(V×E)。

此处不用邻接表或邻接矩阵的原因是不需要，邻接矩阵和邻接表的使用可以方便对边与边连接关系的查找，但此类题目仅一一遍历边即可，因此直接结构体数组比其他方法更加方便。

关于题中有可能存在负圈的情况，可以写一个函数来单独判断一下。（毕竟不停的走负圈可以无限减小，答案肯定要将其排除）
实现原理：如不存在负圈，while(true)的循环最多执行V-1次（最短路必为树，共V-1条边，最差情况是每次都只更新出最短路的一段（每次必更新出一段）），如果存在可到达的负圈，第V次必会更新某一点的值，可以通过此性质来进行判断。

bool find_negative_loop()
{
    memset(d,0,sizeof(d));//随便什么值 
    for(int i=0;i<V;i++)
        for(int j=0;j<E;j++)
        {
            edge e=infor[j];
            if(d[e.to]>d[e.from]+e.cost)
            {
                d[e.to]=d[e.from]+e.cost;
                if(i==V-1) return true;//第V次 
            }
        }
} 

简化写法：把fill写在函数外，先fill(0)，检测负圈，再fill(INF)用于计算。

Bellman-Ford算法是此章介绍的三种算法中唯一能判断负圈和用于负边的算法。（原因在最后解答）。

单源最短路问题2（Dijkstra算法）

对于Bellman-Ford算法，如果d[i]不是最短距离，在它的基础上对d[j]进行更新，d[j]一定不是最短，这就浪费了大量的时间。而且，即使d[i]已是最短边，每一次循环都会再对他判断一次，也是浪费时间的。而Dijkstra算法，就是Bellman-Ford算法的基础上进行了改进，降低了时间复杂度，提高了效率：找到最短距离已经确定的点，从它出发更新相邻点的最短距离。
那么，怎么找到最短距离已确定的点？假设d[i]的值是没确定的点中最小的，那么可知无法通过其他点绕路找到更短的路径。因此，仅需每次找到最短点进行更新即可。

int cost[MAXN][MAXN];//邻接表 
int d[MAXN],V;//最短距离，顶点数 
bool use[MAXN];//标记是否确定
void dijakstra(int s)
{
    int i;
    fill(d+1,d+V+1,INF);//要用min 
    fill(use+1,use+V+1,false);//初始化
    d[s]=0;//已开始起点最短 
    while(true)
    {
        int v=-1;
        for(i=1;i<=V;i++)
        if(!use[i]&&v==-1||d[i]<d[v]) 
            v=i;//找到未确定的最短距离 
        if(v==-1) break;//结束，所有点的最短距离已确定 
        use[v]=true;//最短距离确定 
        for(i=1;i<=V;i++)
            d[i]=min(d[i],d[v]+cost[v][i]);//更新剩下的点的最短距离 
    }
} 

共V个点，每次更新d[i]共V次cost，复杂度O(V²);如用邻接矩阵，cost是E次，但要枚举V次顶点，复杂度依旧是O(V²)。所以可知，如E较小，大部分的时间都花在了查找上，所以此处可用合适的数据结构进行优化。用优先队列查找时，插入取出复杂度为O(logV)，更新和撤入的次数是E次，所以复杂度是O(ElogV)。

struct edge{int to,cost};//结构体 
typedef pair<int,int> P;//前一个为距离，后一个为点 
int d[MAXN],v;
vector<edge> infor[MAXN];
void dijkstra(int s)
{
     priority_queue<P,vector<P>,greater<P> > que;//按first的值从小到大排 
     fill(d+1,d+V+1,INF); 
     d[s]=0;//初始化 
     que.push(P(0,s));//填入 
     while(!que.empty())
     {
         P p=que.top();que.pop();
         int v=p.second;//此时距离最短的点 
         if(d[v]<p.first) continue;         //虽然p.second对应的p.first会有很多值，但第一次被取出时对应的一定是最小，其余的值就可以废弃， 
      // if(use[v]) continue; use[v]=true; //不需再做更新与填入操作，所以直接用continue跳过即可。其实也可以开use数组，对已经标记过的点跳
                                           //过也有同样的效果
         for(int i=0;i<infor[v].size();i++)//填入 
         {
             edge e=infor[v][i];
             if(d[e.to]>d[v]+e.cost)
             {
                 d[e.to]=d[v]+e.cost;//判别式 
                 que.push(P(d[e.to],e.to));
             }
         }
     } 
}

但Dijkstra算法无法应用于存在负边的情况。
好像有个SPFA算法，写到这的时候才知道，后续补。

多元最短路问题（Floyd_Warshall算法）

实际就是dp，从点i到点j有两种走法：1)直接由i到j。2)从i到k再到j。因此递推式：d[i][j]=min(d[i][j],d[i][k]+d[k][j])。代码如下：

int d[MAXN][MAXN];//d[i][i]=0,不存在路径时为INF
int V;
void warshall_floyd()
{
    for(int k=0;k<V;k++)
        for(int i=0;i<V;i++)
            for(int j=0;j<V;j++)
            	d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
}

时间复杂度O(V³)。可以运用于存在负边的情况。

路径还原

路径还原其实很简单，在Dijkstra算法（前面的算法都可以）我们每次更新最小值时，都知from和to，只要要开个数组更新每个点的from值（前驱节点），最后不断寻找前驱点就可以恢复出最短路。复杂度O(E)。
记录路径：

int prev[MAXN];
fill(prev,prev+V,-1);
if(d[i]>d[j]+cost[i][j])
{
    d[i]=d[j]+cost[i][j];
    prev[j]=i;//加入，记录
}

路径还原：

vector<int> get_path(int t)
{
    vector<int> path;
    for(；t!=-1;t=prev[t]) path.push_back(t);//不断沿着prev[t]走直到s
    reverse(path.begin(),path.end());
    return path;
}

开始写的时候以为什么都懂了，结果又在某些地方卡了好久，蒟蒻绝望。

负边、负圈情况

在Bellman-Ford算法中，每个顶点的所有入度都被考虑，所以无论正边负边都无关紧要，负圈作为特殊情况可被检测出。
Floyd_Warshall算法同上，但不可检测负圈。
而在Dijkkstra算法中，对于已确定的最短路径，无法再度进行修改，但若有负圈存在，无法确定每次找到的是否是最短距离，反例：

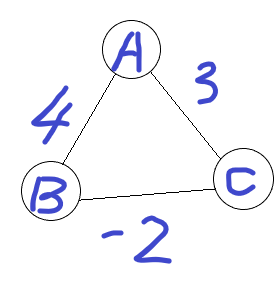
由A到C的最短距离应为2，而Dijkstra算法只能取3。负圈就更不用说了。

可以处理负边的SPFA

SPFA，即shortest path faster algorithm。是一种可以处理负边的算法，是Bellman-Ford算法的升级版，这里只建议在有负边存在的时候使用，其余情况用Dijkstra最好。
SPFA用队列来保存待优化的节点（仅节点，不存值）第一次塞入起点，此后每次操作取出第一个节点，对它可到达的所有点进行一次更新(即Bellman-Ford的方法)，如此点成功更新且不在队列内，将其加入队列（更新成功说明在走当前点的情况下还有更短的可能，未来存在再次更新的可能性；如未成功，说明原值更短，即使有最短路径也不会从当前点经过，所以不填入），直到队列空结束（所有点都无法在更新，已最短）。
代码：

bool vis[MAXN];//判断是否在队列 
queue<int> q; 
int mp[MAXN][MAXN];//邻接表，无法到达为INF 
int dp[MAXN];//最短路 
int update[MAXN];//更新次数
int V,E;//角，边 
bool flag;
void spfa(int s)
{
    fill(dp+1,dp+1+v,INF);
    dp[s]=0;
    q.push(s);//塞入起点 
    vis[s]=true;//标记 
    while(!q.empty())
    {
        int t=q.top();q.pop();
        vis[t]=false;
        for(i=1;i<=V;i++)
            if(dp[i]>dp[t]+mp[t][i])//可更新 
            {
                dp[i]=dp[t]+mp[t][i];//将其更新 
                update[i]++;
                if(update[i]>V) flag=true;//出现负环
                if(!vis[i])//不在队列 
                {
                    q.push(i);//塞入 
                    vis[i]=true;//标记 
                }
           }
     }
     if(flag) break;//负环结束
} 

如果某一个点被更新了V次，即存在负圈。检测跳出后队列是否为空，即可判断是否有负环

存在负边的多源最短路问题（Johnson算法）

多源最短路不仅可以用Floyd_Warshall算法解决，也可以多次使用Dijkstra来实现，但若存在负边且Floyd不幸被卡时，就要用到当前所说的Johnson来操作了。Johnson算是SPFA与Dijkstra的融合。Johnson算法运用了“重赋权”技术，即将原图中每条边的权值ω重新赋值为ω’，并且具有以下两个性质：1.对所有顶点对u,v，路径p是以权值为ω的原图的最短路径，当且仅当路径p也是以权值为ω’的图的最短路径；2.所有的边(u, v)，ω’(u, v)是非负数。此操作使用SPFA+特殊处理实现的。重赋权后的图可以利用Dijkstra算法求解任意两个顶点之间的最短路径。重赋值不会改变最短路径，其处理复杂度为O(VE)。
关于为何如此重赋值以及重赋权操作后的性质为何成立我在这不予证明，可以到此来了解。
具体操作：额外设置一个点（比如0点），并将它到其余各点的权值设为0。用SPFA求此点到其余点的最短距离，并记录，也可判断是否存在负圈。重赋值操作：ω’(u, v) = ω(u, v) + h(u) – h(v)。此后再用Dijkstra计算即可。

int h[MAXN];//存从0到各边的最短路
for(int i=0;i<V;i++)
	mp[0][i]=0;
SPFA
for(int i=0;i<V;i++)
	for(int j=0;j<V;i++)
		mp[i][j]+=h[i]-h[j];
Dijkstra