统计学完全教程(All of Statistics)第九章习题

最新推荐文章于 2023-09-13 18:53:23 发布

klinfelter

最新推荐文章于 2023-09-13 18:53:23 发布

阅读量2.2k

点赞数 1

文章标签： python 概率论

本文链接：https://blog.csdn.net/weixin_43851599/article/details/128198520

版权

这一章的习题第3题，第一次见到对0.95分位数求极大似然估计的题目，看上去很复杂但是道理都是一样的。

原题是这样的：

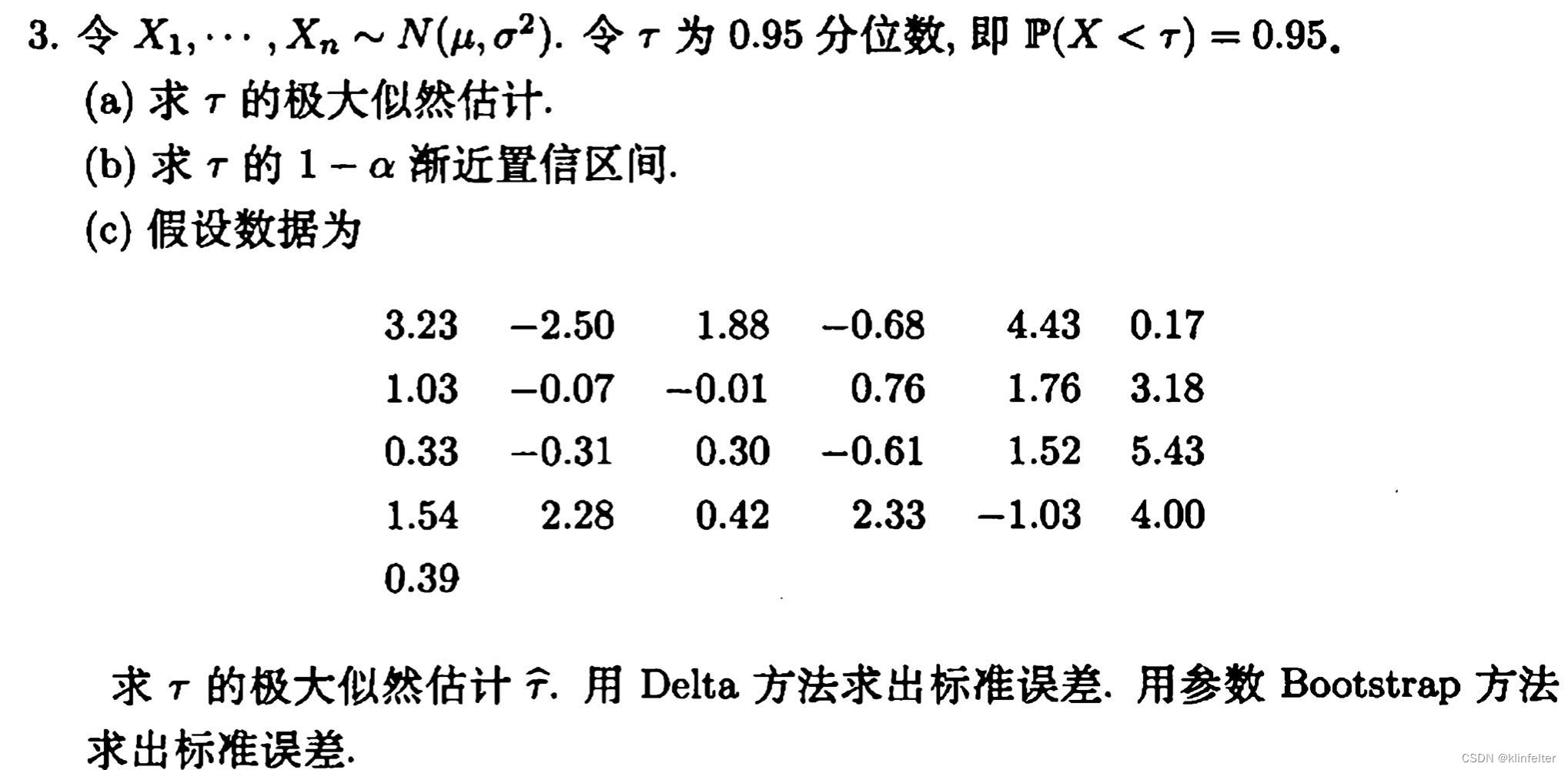
前两问就是按极大似然估计法的思路求解，先求出 $\mu$ 和 $\sigma$ 的极大似然估计 $\hat{\mu}$ 和 $\hat{\sigma}$ ，再根据我们解出的 $\tau$ 关于这两者的表达式得到 $\tau$ 的极大似然估计。

(a).

$\begin{cases} \hat{\mu} = \bar{X} \\ \hat{\sigma}^2 = \tfrac{1}{n} \sum_{i=1}^{n}(X_i - \bar{X})^2 \end{cases}$

$P(X<\tau) = P\left ( \tfrac{X-\mu}{\sigma} <\tfrac{\tau - \mu}{\sigma} \right ) = 0.95$ 解得 $\tau = \sigma \cdot z_{0.05}+ \mu$ $\therefore \hat{\tau} = \hat{\sigma}\cdot z_{0.05} + \hat{\mu}$

(b).

$I_n(\theta) = -E(\frac{\partial^2 ln(\theta)}{\partial \theta \partial \theta^T}) = -\begin{pmatrix} E(\frac{\partial^2 ln(\theta)}{\partial \mu^2}) & E(\frac{\partial^2 ln(\theta)}{\partial \sigma \partial \mu})\\ E(\frac{\partial^2 ln(\theta)}{\partial \sigma \partial \mu}) & E(\frac{\partial^2 ln(\theta)}{\partial \sigma^2}) \end{pmatrix} = \begin{pmatrix} \tfrac{n}{\sigma^2} & 0\\ 0 & \tfrac{2n}{\sigma^2} \end{pmatrix}$

$J_n(\theta) = I_n^{-1}(\theta) = \begin{pmatrix} \tfrac{\sigma^2}{n} & 0\\ 0 & \tfrac{\sigma^2}{2n} \end{pmatrix}$

令 $g(x, y) = x+z_{0.05}\cdot y$ ，有 $\triangledown g = (1, z_{0.05})^T$

$\hat{se^2 (\hat{\tau})} = \triangledown g^T\cdot J_n(\theta)\cdot \triangledown g = (1, z_{0.05})\begin{pmatrix} \tfrac{\hat{\sigma}^2}{n} & 0\\ 0 & \tfrac{\hat{\sigma}^2}{2n} \end{pmatrix} \begin{pmatrix} 1 \\ z_{0.05} \end{pmatrix} = \frac{\hat{\sigma}^2}{n} + z_{0.05}^2\cdot \frac{\hat{\sigma}^2}{2n}$

$\tau$ 的 $1-\alpha$ 置信区间 $C_n = (\hat{\tau}\pm z_{\frac{\alpha}{2}}\cdot \hat{se(\hat{\tau})})$

(c).

# All of Statistics: Chapter 9
import numpy as np
import math
from scipy.stats import norm

# Q3(c)
x = [3.23, -2.50, 1.88, -0.68, 4.43, 0.17, 1.03, -0.07, -0.01, 0.76, 1.76, 3.18, 0.33, -0.31, 0.30, -0.61, 1.52, 5.43, 1.54, 2.28, 0.42, 2.33, -1.03, 4.00, 0.39]
x_ba = np.mean(x)
var_hat = np.var(x)
z_005 = norm.ppf(q = 1-0.05, loc = 0, scale = 1)
tau_hat = z_005 * np.std(x) + x_ba
se_hat = math.sqrt(var_hat / 25 + var_hat / 50 * z_005 ** 2)

y = np.random.normal(loc = x_ba, scale = np.std(x), size = 25)
def T_F(data):
    mu = np.mean(data)
    sigma = np.std(data)
    return z_005 * sigma + mu

def bootstrap_replicate_1d(data, func):
    bs_sample=np.random.choice(data, len(data))
    return func(bs_sample)

def bootstrap_res(data, func, size=1):
    bs_replicates = np.empty(size)
    for i in range(size):
        bs_replicates[i] = bootstrap_replicate_1d(data, func)
    return bs_replicates

B_hat = bootstrap_res(y, T_F, size = 10000)
se_boot = np.std(B_hat)

print("\n MLE = ", tau_hat, "\n", "se_Delta = ", se_hat, "\n", "se_boot = ", se_boot)

Delta方法求出的标准差是唯一确定的，Bootstrap方法求出的标准差是不唯一的。