1.问题引入
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
eg:

2.动态规划特点

动态规划遵循一套固定的流程:递归的暴力解法 -> 带备忘录的递归解法 -> 非递归的动态规划解法。
3.递归解法
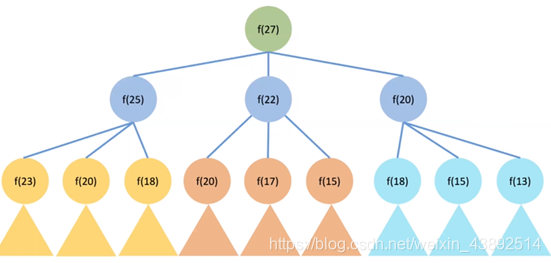
// 多叉树遍历/递归解法
class Solution {
public:
// 目标金额amount时,返回需要最少的硬币个数
int coinChange(vector<int>& coins, int amount) {
if (amount == 0) {
return 0;
}
int ans = INT_MAX;
// 多叉树遍历
for (auto coin : coins) {
// 金额不可达
if (amount - coin < 0) {
continue;
}
int subProb = coinChange(coins, amount - coin);
// 子问题无解
if (subProb == -1) {
continue;
}
ans = min(ans, subProb + 1);
}
return (ans == INT_MAX) ? -1 : ans;
}
};
存在的问题:

4. 备忘录消除重复计算:自顶向下
// 方法三:带备忘录的解法
class Solution {
public:
// 目标金额amount时,返回需要最少的硬币个数
int coinChange(vector<int>& coins, int amount)
{
vector<int> memo(amount + 1, -2);
return helper(coins, amount, memo);
}
int helper(vector<int>& coins, int amount, vector<int>& memo)
{
if (amount == 0) {
return 0;
}
if (memo[amount] != -2) {
return memo[amount];
}
int ans = INT_MAX;
for (auto coin : coins) {
if (amount - coin < 0) {
continue;
}
int subProb = helper(coins, amount - coin, memo);
// 子问题无解
if (subProb == -1) {
continue;
}
ans = min(ans, subProb + 1);
}
// 记录本轮结果
memo[amount] = (ans == INT_MAX) ? -1 : ans;
return memo[amount];
}
};
5.动态规划步骤:自底向上
// 动态规划
class Solution {
public:
int coinChange(vector<int>& coins, int amount)
{
vector<int> dp(amount + 1, amount + 1);
dp[0] = 0;
// 外层for 循环遍历所有状态
for (int i = 1; i < amount + 1; i++) {
// 内层 for 在求所有子问题 + 1 的最小值
for (auto coin : coins) {
// 金额不可达
if (i - coin < 0) {
continue;
}
dp[i] = min(dp[i], 1 + dp[i - coin]);
}
}
return dp[amount] == amount + 1 ? -1 : dp[amount];
}
};
第一步:确定状态

第二步:确定转移方程
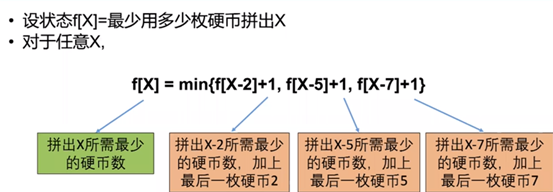
第三步:确定初始条件和边界情况

第四步:确定计算顺序
原则:当要计算等式左边F(X)是,右边的应该都已经计算出来了
1、遍历的过程中,所需的状态必须是已经计算出来的。
2、遍历的终点必须是存储结果的那个位置。

小结






 本文探讨了硬币兑换问题的解决方案,通过递归、带备忘录的递归及动态规划三种方法,逐步优化算法效率。介绍了如何使用动态规划解决硬币兑换问题,包括状态定义、转移方程、初始化条件和计算顺序。
本文探讨了硬币兑换问题的解决方案,通过递归、带备忘录的递归及动态规划三种方法,逐步优化算法效率。介绍了如何使用动态规划解决硬币兑换问题,包括状态定义、转移方程、初始化条件和计算顺序。
















 989
989

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








