-
参数计算基础
Transformer-block基本参数计算

假设,隐层维度为h,SA就有四个h * h的权重和对应的偏置:4h² + 4h
MLP:两层,h * 4h,偏置4h 和 4h * h ,偏置h: 8h² + 5h
LN: 一个α一个β,2h,但是一个Block中有两个LN,所以是4h
所以每个block就是 12h² + 11h(图中为13h)
假设有L层,那么total参数量:L*(12h² + 11h),当h够大时,12h² >> 11h
所以总参数量可估算为L * 12h²
根据该公式,可估算Llama的参数量

可以看到误差并不大,很接近。 当然这里没有算Embedding和输出层的参数
模型浮点运算总量(FLOPs)的计算
首先区分一个概念 FLOPS和FLOPs

计算示例

假设x和y均是m维的向量,每一次加减乘除算作一次float运算
那么xy相乘时,首先逐个元素相乘,m次运算,再做m-1次加法运算,一共是2m-1次运算≈2m
拓展成矩阵,假设A : m * n 。B:n * 1, 那么相当于 要做m次 两个n维向量相乘的操作,就是m*2*n
假设B:n*r,以此类推:m * 2 * n * r FLOPs
SA 的计算

首先是Wq,Wk,Wv 做得操作均是 b,s,h * h*h = 2h* b * s *h = 2bsh²
三个,就是6bsh²
QK:不考虑batch下: s,h * h,s :2h*s*s = 2hs²,乘上batch就是 2bhs²
Softmax(*) * V = 同理 2bhs²
最后一个线性变化,同Wqkv:2bsh²
总:8bsh²+4bhs²
MLP计算

第一层MLP: b s h, h 4h: b * s * 2h * 4 *h = 8bsh²
第二层MLP: b s 4h , 4h * h:b * s * 2 * 4h *h = 8bsh²
输出层: b s h , h * V(词表长度) : b * s * 2h *V = 2bshV
假设模型有L层,那么就是 L * (SA FLOPs + MLP FLOPs) + 2bshV
= L *(24bsh²+4bs²h)+2bshV
这是针对一个batch的计算量
由于h² >> s²,所以可以近似为:L*24bsh²
计算量和参数量的关系

运算数/参数量 = L * 24bsh² / 12Lh² = 2 bs = 2 * tokens
有 运算量 /参数量/ tokens = 2 , 等于说在forward的过程中,对于每个token,每个模型参数,需要两个float运算。
在backward的过程中,将某些中间结果存起来是最高效的,但是会占用大量显存,所以一般是会做一些重复运算操作,用时间换空间,大概运算量是Forward的两倍。 此外中间变量计算大概等于forward。 所以整个训练流程就是 对于每个token 每个参数,需要进行2 * 4 = 8个float运算
由此,我们知道模型参数,训练token数量,显卡数量,显卡性能情况下可以估算训练时间
模型训练时间的估算

训练时间等于FLOPs / 显卡算力
= 8 * tokens *参数量 / ( GPU_NUMS * FLOPS * GPU利用率)
关于显卡的FLOPS,根据模型参数是fp16还是fp32来看单精度/半精度下的算力
实例:
计算GPT3.5在1024张A100训练300Btoken

注意 由于是多卡并行。GPU使用率一般在40%~50%
且这里没考虑CPU读写时间,所以比真实时间还是要短一些
Flash Attention
计算机基础-佛诺依曼架构

计算机中大大小小的单元,比如cpu,gpu,都是通过主板,一根根线来组装得到,就是Host BUS,叫做总线
左侧是cpu部分,数据从硬盘,通过总线到内存中,再从内存中加载到CPU的cache中,再从各级cache逐级加载到CPU Core(计算单元),计算完后再存储到内存中,如果内存中装不下,就会存到硬盘
右侧是GPU
gpu详细结构

在计算Attention的时候,设QKV的lenght为N,那么时间复杂度(N,D和D,N做矩阵运算)和空间复杂度(N*N的结果矩阵需要存在显存中)都是O(N²)

优化这个问题,有两个出发点

一个是优化计算速度(当length增加时,计算复杂度是指数级增长),一个是如何节省显存(O(N²)->O(N)),flash attention作者认为传输代价是大于计算代价的,所以要去避免将O(N²)的数据频繁做读写

再者,目前对attention的优化都是基于近似计算的,比如Sparse Attention,如何在保证精确计算的同时去优化速度和显存占用是一个问题

相关硬件读写速度: SRAM > GPU HBM(显存) > DRAM(cpu内存)
右图中,当我们计算A B C D时,首先将ABCD load进HBM中,然后HBM先将AB放入SRAM,SRAM再将其放到计算单元中计算,得到AB计算的中间结果S,然后S-> SRAM->HBM中,然后再从HBM中将S和C送入SRAM再计算,以此类推
时间消耗分为两块,(1)计算的时间(计算单元内的计算),(2)通信的时间(a. 计算单元<->SRAM,b. SRAM<->HBM)。 时间消耗主要在b

如图,在计算Attention的时候,QK计算的结果S会存入HBM,Softmax的结果P会存入HBM, PV的计算结果也会存入HBM
将中间结果存入HBM的过程去除,尽量让整个计算pipeline在计算单元和SRAM中进行。这就是FlashAttention解决的事情
如图右下角,QKV被分成了一个个小矩阵,每个对应位置的小矩阵的计算均在SRAM中进行。最后每组小矩阵计算完的结果再一起reduce到HBM中
SA计算回顾
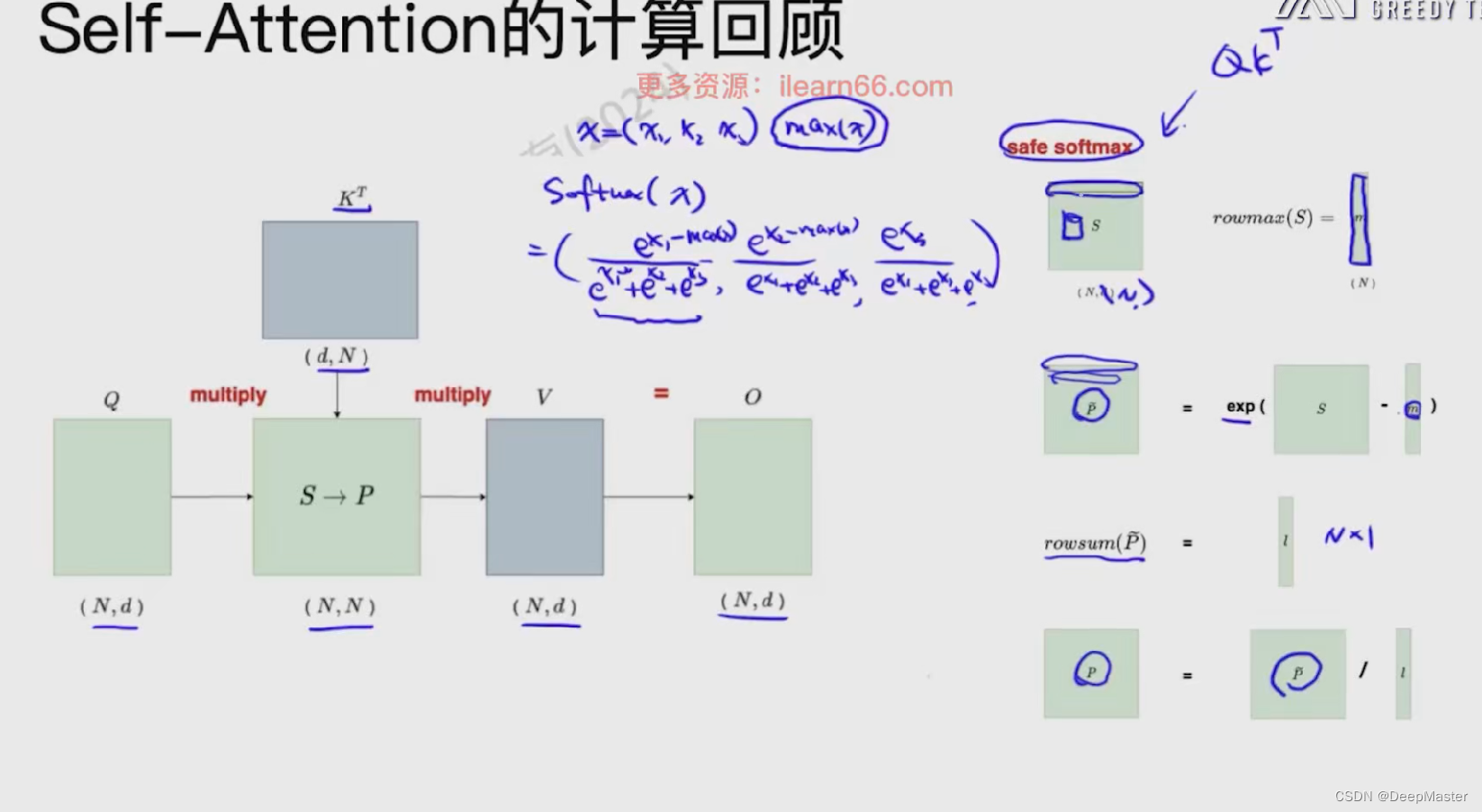
Safe-softmax
这里要注意的是safe softmax的操作
softmax中,指数计算exp存在不稳定性,比如数值容易溢出,超过一定范围计算精度会下降等问题。因此在实际使用中,往往用safe softmax更好,safe softmax的计算是在navie softmax的基础之上将数组x[1…n]每个元素减去数组的最大值max之后,再做softmax
如图中右侧所示,softmax操作是逐行进行的,首先求出每行的最大值,得到一个向量,然后用原attention矩阵减去这个向量,相当于是每行元素减去对应的最大值,然后再取对数,就得到了softmax中的分子。 然后再求取每行的和,得到一个向量l,这个就是分母。 然后p再除以l就得到最终的结果
基本思想-分块计算

举个例子,首先对Q K V矩阵进行分块操作,将Q矩阵按照length划分成四份,设Br = N //4. 那么每一份就是Br x d, 对K矩阵划分成三份,设Bc = N//3,那么每份就是Bc x d,转置之后就是d x Bc.
V的切分方式和K保持一致,每份是Bc x d,输出为O,O矩阵形状和K一致,划分方式也是一致的
由于我们想保持一个并行操作,所以是按照列进行操作,设注意力得分矩阵是S,那么就是先填充第一列,再填充第二列... 计算的过程可以是一个双层for循环,外层是K的列索引j = 1~3, 内层就是Q的行索引1~4, 如图左上角。
图中S矩阵中S21部分,是由Q2矩阵和K1矩阵得到的,假设input是一个有12个token的句子
I like this movie very much but the ticket is very expensive
那么Q2就代表 movie very much
K1 代表 I like this moive , 那么S21就代表movie very much 对I like this moive的注意力,还缺少对剩余8个token的注意力。此时用S21进行softmax再 乘以V1 就得到O2(由于计算到S21时,S22, S23都还没计算,为0)。那么此时O2肯定不是我们想要的。首先S21softmax 的结果是局部的结果,并不是S21所在几行的准确结果,且不包含Q2中这几个token对于全句子的注意力信息。
所以我们要做的就是逐步迭代S矩阵,让其计算出来的softmax逐渐趋于准确,且让O矩阵逐步得到正确结果

假设x(1)为S中第一列一个分块矩阵,设m(x)为全局最大值,m(x(1))就为分块1的最大值,设f(x)为softmax的分母:exp(x - m(x)),那么对应分块1 就是exp(x(1) - m(x(1))), 设L(x)为全局的rowsum,
那么x(1)的row sum就是L(x(1)) = sum(exp(x - m(x) ) )
当得到x(2)之后,全局的值怎么变化呢?
首先是m(x) = max(m(x1), m(x2) ), 比如m(x1)是3,m(x2)是5,分子中每项再要多减去2,再取对数,其实就是再乘以e-2,那么就是在原来分子的基础上再乘以exp(m(x1) - m(x))
那么此时f(x)就变成 = [exp( m(x1) -m(x) ) * f(x1) , exp( m(x1) -m(x) ) * f(x2)]
分母同理,也是乘上相同的指数函数:
L(x) = [exp( m(x1) -m(x) ) * L(x1) + exp( m(x1) -m(x) ) * L(x2)]
那么这个时刻的softmax的结果就是用f(x) / L(x) 。再乘上对应的V分块矩阵,就能更新对应O中分块矩阵的结果了
下面是一个计算的实例

右侧是第一个分块矩阵和第二个分块矩阵的m L f 函数的计算,以及m函数的更新
左下角是m更新好了之后对当前第一个分块矩阵所在这两行的全局f(x) L(x)做更新
Flash attenion的算法伪代码

关于倒数第二步中,如何将Oi得出,步骤:


(更改一下 
图片中的m~ 其实是当前Si,j,也就是attention矩阵中那一个小块里的row_max,并不是全局row_max
)
准确的说是得出Oi,j 就是Oi的第j次更新的结果。
我们在迭代的过程中,存储每个i下的L(row_sum),m (row_max),还有O
这个公式就是通过利用j-1时刻的L,m,O和当前j下计算的最新的L,m,还有当前softmax的分子P来计算当前j下的O,通过这种方式来循环更新O,最终得到准确的计算结果
所以每一个Oi,j 仅依赖Oi,j-1,并不用存储之前所有的数据
KV Cache
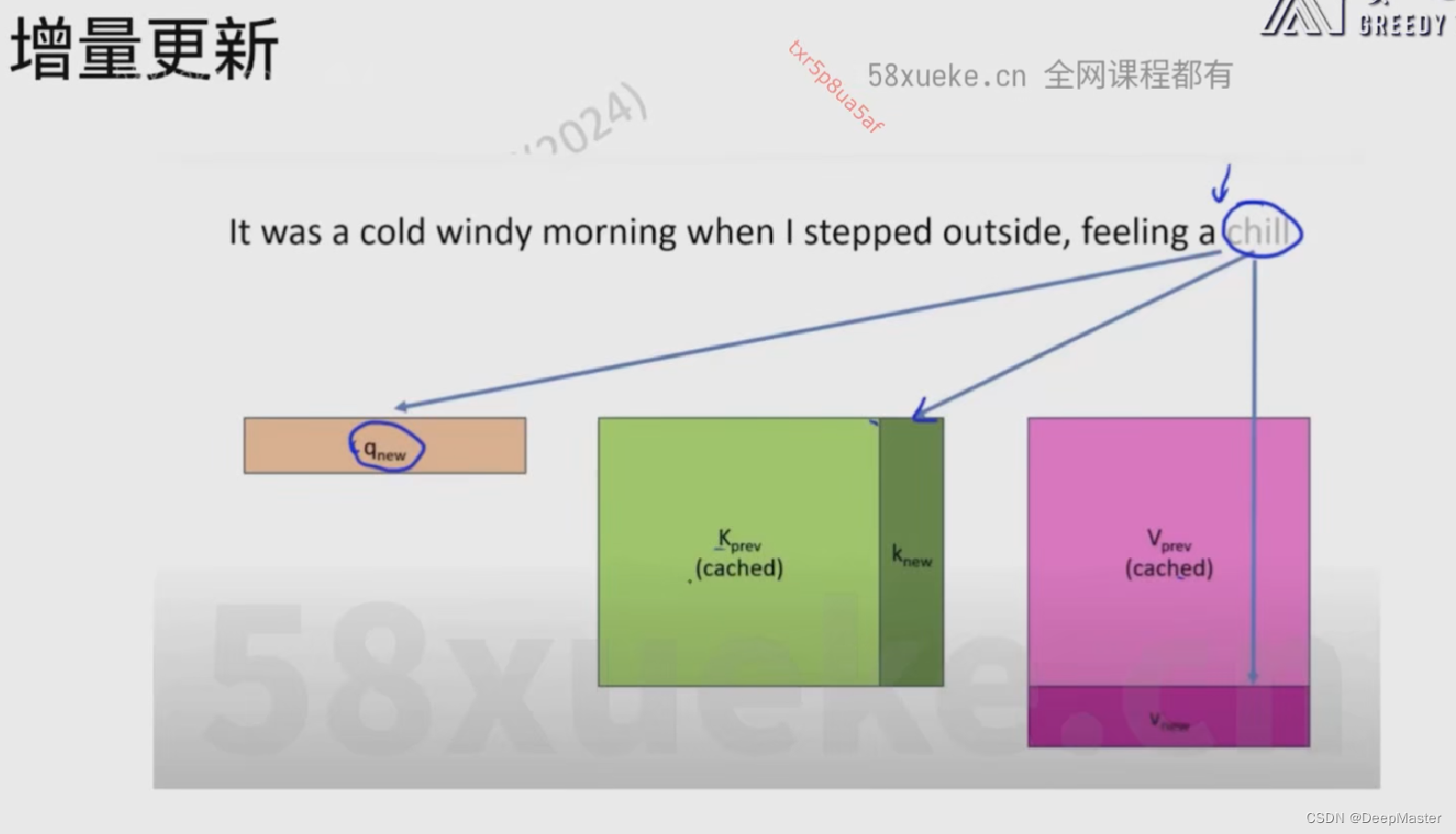
这个后面再补充

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








