学过空间插值的人都知道和反距离插值(IDW)和克里金插值， 本文讲简单介绍基本克里金插值的原理，以及在Arcgis中实现的详细过程。由于IDW操作和克里金很相似，并且最常用的是克里金，因此实操部分给了克里金的。读者可以根据如下教程摸索IDW是完全可以的呢。
一、反距离插值(IDW)
空间插值问题，就是在已知空间上若干离散点 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi)的某一属性(如气温，PM2.5浓度)的观测值 z i = z ( x i , y i ) z_{i}=z\left(x_{i}, y_{i}\right) zi=z(xi,yi)的条件下，估计空间上任意一点 ( x , y ) (x, y) (x,y)的属性值的问题。
地理属性有空间相关性，相近的事物会更相似。由此人们发明了反距离插值，对于空间上任意一点
(
x
,
y
)
(x, y)
(x,y)的属性
z
=
z
(
x
,
y
)
z=z(x, y)
z=z(x,y), 定义反距离插值公式估计量
z
^
=
∑
i
=
1
n
1
d
α
z
i
\hat{z}=\sum_{i=1}^{n} \frac{1}{d^{\alpha}} z_{i}
z^=i=1∑ndα1zi
其中
α
\alpha
α通常取1或者2。
用空间上所有已知点的数据加权求和来估计未知点的值，权重取决于距离的倒数（或者倒数的平方）。那么，距离近的点，权重就大；距离远的点，权重就小。
- 但是通常 α \alpha α的值通常不确定
- 用倒数来描述空间的关联程度不够准确
从而提出了克里金插值法
二、克里金插值法
克里金斯插值的优势:
-
在数据网格化的过程中考虑了描述对象的空间相关性质，使插值结果更科学、更接近于实际情况；
-
能给出插值的误差（克里金方差），使插值的可靠程度一目了然
克里金插值的公式
z
^
o
=
∑
i
=
1
n
λ
i
z
i
\hat{z}_{o}=\sum_{i=1}^{n} \lambda_{i} z_{i}
z^o=i=1∑nλizi
其中
z
^
o
\hat{z}_{o}
z^o是点
(
x
o
,
y
o
)
\left(x_{o}, y_{o}\right)
(xo,yo)处的估计值，即
z
o
=
z
(
x
o
,
y
o
)
z_{o}=z\left(x_{o}, y_{o}\right)
zo=z(xo,yo) 。
这里的
λ
i
\lambda_{i}
λi是权重系数。它同样是用空间上所有已知点的数据加权求和来估计未知点的值。但权重系数并非距离的倒数，而是能够满足点
(
x
o
,
y
o
)
\left(x_{o}, y_{o}\right)
(xo,yo)处的估计值
z
^
o
\hat{z}_{o}
z^o与真实值
z
o
z_{o}
zo的差最小的一套最优系数，即
min
λ
i
Var
(
z
o
^
−
z
o
)
\min _{\lambda_{i}} \operatorname{Var}\left(\hat{z_{o}}-z_{o}\right)
λiminVar(zo^−zo)
同时满足无偏估计的条件
E
(
z
o
^
−
z
o
)
=
0
E\left(\hat{z_{o}}-z_{o}\right)=0
E(zo^−zo)=0
三、 Arcgis实际操作
3.1 插值实操 - 以克里金为例
- 首先加载
数据和底图
数据要包含经纬度信息和需要插值的浓度，这里以2018年长三角PM2.5为例
-
右键 - 显示经纬度
-
打开工具箱
spatical Analysis Tools - Interploation - IDW
- 克里金插值设置
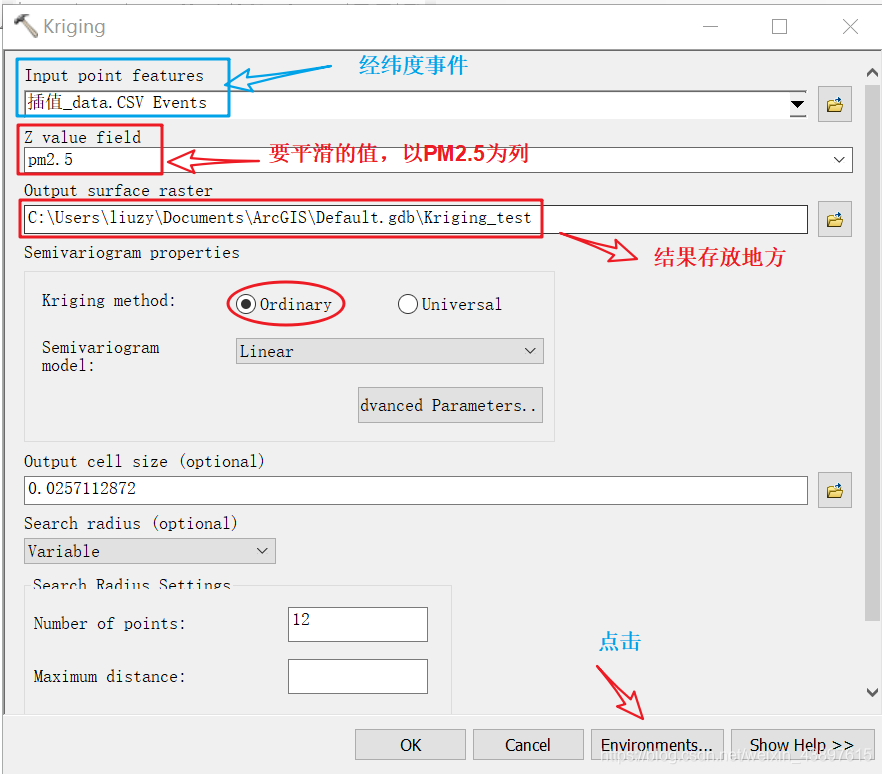
第一点：处理范围
第二点：栅格分析
四、出图
为了美化作图，而进行了页面设置-出图如下
如果你有问题，请随时发表评论。
码字不易，如果你觉得有用，请帮忙点个赞或者关注。
扫一扫
2万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
