本文将根据克里金插值的原理,在matlab中逐步进行运算,之后在arcgis中进行克里金插值,并将两种计算方法的结果进行对比。
一、克里金原理
,
,....,
为区域上的一系列观测点,
,
,...,
为观测得到的值。现在想求得
处的值
。设
的估计值为
克里金插值将空间中所有已知点的数据加权求和,来估计未知点的值,其计算公式如下:
其中是权重系数。
假设空间属性z是均一的,对于空间任意一点 (x, y),其期望c和方差是相同的。即:
普通克里金插值需满足两点假设:无偏和最优。
① 无偏:所有位置的期望值相同,则
将 和
代入,得
② 最优:估计方差最小,则
根据一系列公式推导,得到方程组,矩阵形式如下:
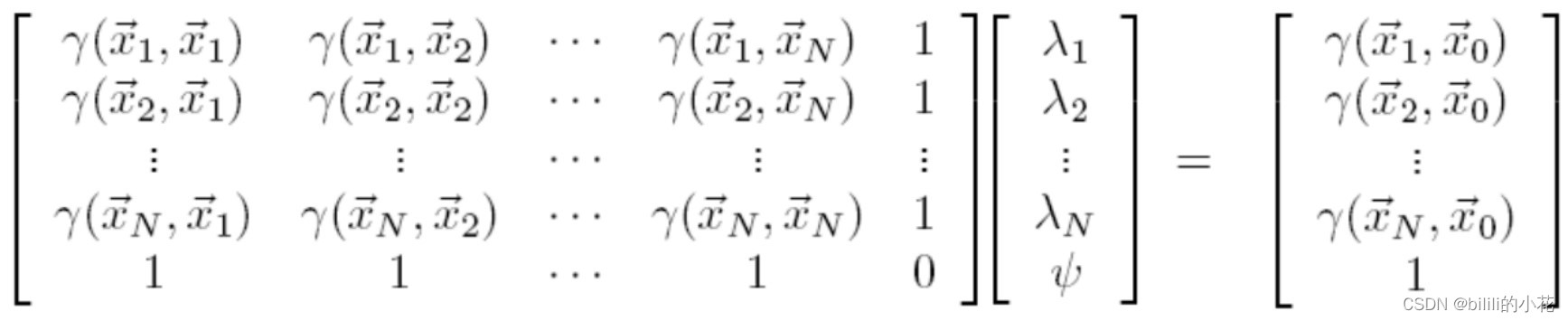
其中 为各点对应的权重系数,
为半方差函数。对方程求解,得到最优系数
,再代入公式
中即可位置点的估计值。
由地理学第一定律,空间越相近属性越相似。克里金插值假设与
存在某种函数关系,该函数关系可以是线性、二次函数、指数、对数等。根据已有数据集拟合得到函数后,对于任意两个点,先计算其距离,即可得到两点的半方差。
二、利用模拟案例逐步计算ordinary kriging
具体进行计算时,首先获得观测数据。在Arcgis中随机生成130个点,并读取其经纬度和对应的dem值。

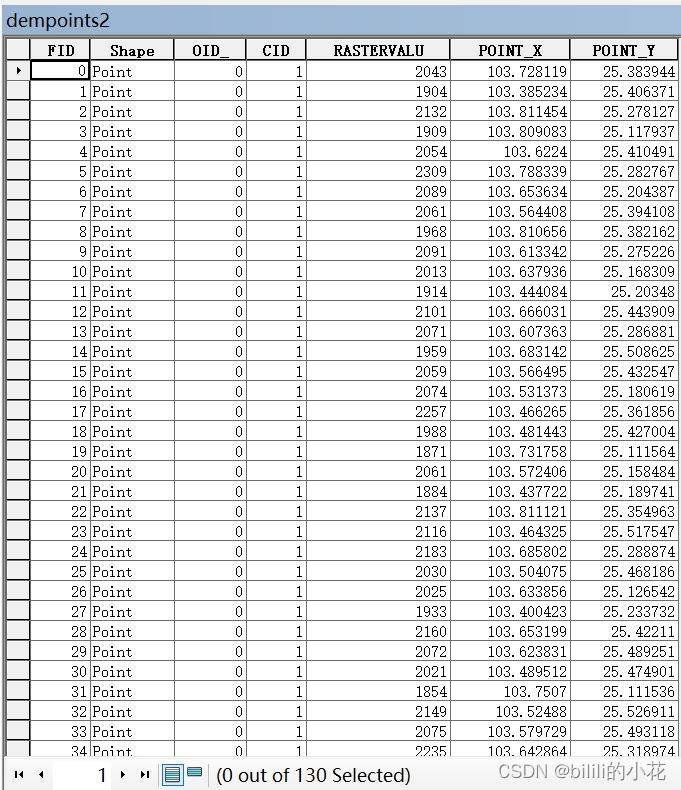
matlab读取dbf,根据平均数和标准差去除异常值,并检验正态分布情况。代码如下:
[NUM_site,~,~]=xlsread('D:\...\dempoints2.dbf');
% 去除异常数据
mean_DEM = mean(NUM_site(:,3));
std_DEM = std(NUM_site(:,3));
data = [];
for i = 1:length(NUM_site(:,3))
if NUM_site(i,3)<(mean_DEM+2*std_DEM) && NUM_site(i,3)>(mean_DEM-2*std_DEM)
data = [data;NUM_site(i,:)];
end
end
histogram(data(:,3));根据生成的直方图,发现符合正态分布,可以进行进一步计算。
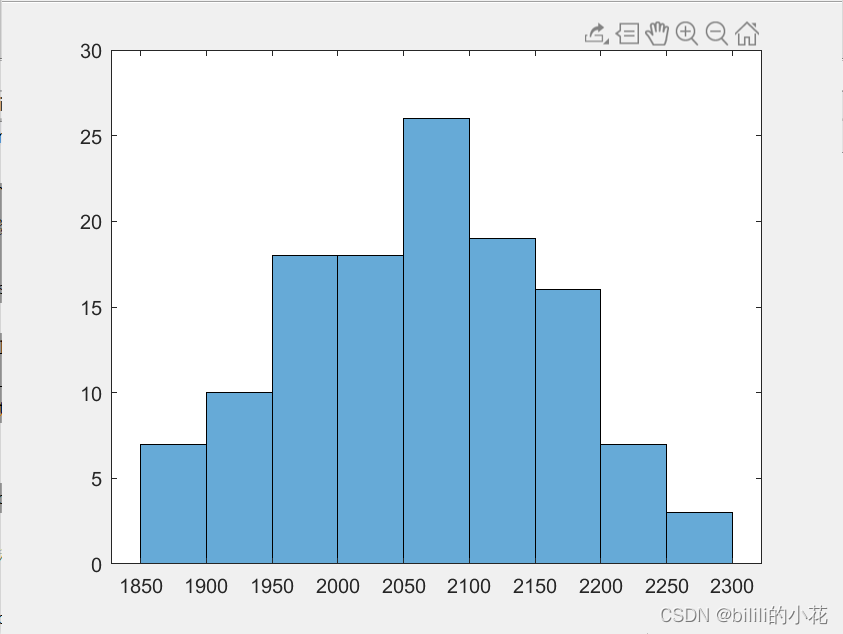
之后,分别计算两个点之间的距离和半方差。距离计算方法为,半方差的计算方法为
。代码如下:
% 计算距离和半方差
distance = [];
semivariance = [];
for i = 1:length(data(:,3))
xi = data(i,4);
yi = data(i,5);
zi = data(i,3);
for j = 1:length(data(:,3))
if j < i
xj = data(j,4);
yj = data(j,5);
zj = data(j,3);
distance = [distance;sqrt((xi-xj)^2+(yi-yj)^2)];
semivariance = [semivariance;0.5*(zi-zj)^2];
end
end
end之后,将计算得到的距离和半方差按照距离从小到大排序,并分成n组(这里分成50组),计算每组内数据的距离平均值和半方差平均值。将散点图绘制在坐标系中。代码如下:
% 按顺序重新排序
known_points = [distance,semivariance];
known_points2 = sortrows(known_points);
% 分段
max_dist = max(distance);
min_dist = min(distance);
n = 50;
interv = (max_dist - min_dist)/n;
dist_aver = [];
semi_aver = [];
for p = 1:n
count = 0;
dist_sum = 0;
semi_sum = 0;
for q = 1:length(known_points2)
if known_points2(q,1) > (min_dist+(p-1)*interv) && known_points2(q,1) <= (min_dist+p*interv)
count = count + 1;
dist_sum = dist_sum + known_points2(q,1);
semi_sum = semi_sum + known_points2(q,2);
end
end
dist_aver = [dist_aver, dist_sum/count];
semi_aver = [semi_aver, semi_sum/count];
end观察散点图,发现距离在0-0.1的区间范围内,数值快速上升,数值在0.1距离范围后数值上升放缓,变程为0.35左右。图像符合“快速上升,之后趋于平稳”的图像趋势。

因此,将最大滞后距设置为0.35,重新生成散点图,改动的代码如下:
max_dist = 0.35;生成图像如下:
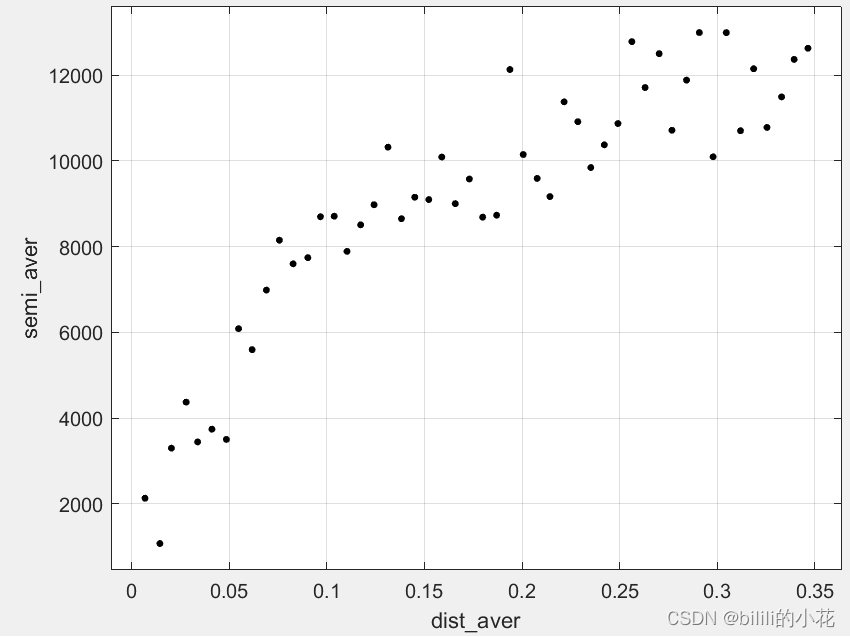
之后在matlab的“curve fitting”拟合工具箱中拟合变异函数。这里尝试球状模型、高斯模型和指数模型。
球状模型拟合结果如下:

指数模型拟合结果如下:

高斯模型拟合结果如下:

比较三个函数拟合结果,综合考虑选择指数作为拟合函数,其R2满足模拟精度要求。
之后,重新计算已知点之间两两距离,代入拟合函数中求每两点之间半方差,代码如下:
% 计算距离和半方差
n = length(data(:,3));
semivariance = ones(n+1);
for i = 1:n
xi = data(i,4);
yi = data(i,5);
for j = 1:n
if j == i
semivariance(i,j) = 0; % 距离为0时半方差设为0
elseif j < i
xj = data(j,4);
yj = data(j,5);
distance = sqrt((xi-xj)^2+(yi-yj)^2);
% 通过拟合函数计算半方差
semivariance(i,j) = 851.2 + 11380*(1-exp(-9.505*distance));
semivariance(j,i) = semivariance(i,j);
end
end
end
semivariance(n+1,n+1) = 0;得到两两之间点的半方差矩阵:

之后,随机选择一个未知点(103.5,25.35),计算未知点到已知点的距离,并代入拟合函数求得半方差,代码如下:
% 计算未知点
x0 = 103.5;
y0 = 25.35;
semivariance2 = [];
for i = 1:n
xi = data(i,4);
yi = data(i,5);
distance = sqrt((xi-x0)^2+(yi-y0)^2);
semivariance2 = [semivariance2; 851.2 + 11380*(1-exp(-9.505*distance))];
end
semivariance2 = [semivariance2;1];得到的半方差如下:

根据下列方程,使用matlab求解矩阵方程组,得到。

matlab代码如下:
x = semivariance\semivariance2;结果如下:

根据下列公式,使用最优系数对已知点的属性值加权求和,得未知点估计值。
代码如下:
x(end,:)=[];
z = sum(data(:,3).*x);算得模拟点的估计值为2165.97m。
代入原栅格中,该位置原数据为2187m,相对误差为0.96%,准确性较高。

三、用软件对实际数据进行kriging插值
本节使用上一节中使用的点数据进行操作。
使用的插值软件是Arcgis中的Geostatistical Analyst。
在对数据进行插值之前,先判断数据是否符合正态分布。选择Geostatistical Analyst -- Histogram。经检验,发现数据符合正态分布,可以进行下一步计算。

选择普通克里金,点击下一步,可以查看半变异函数的设置。其中红色点表示计算的两点之间的半方差,蓝色十字架表示其平均值,蓝线是估计的半方差模型。该模型可用于定义权重,确定每个观测数据对新数据预测的值的贡献度。
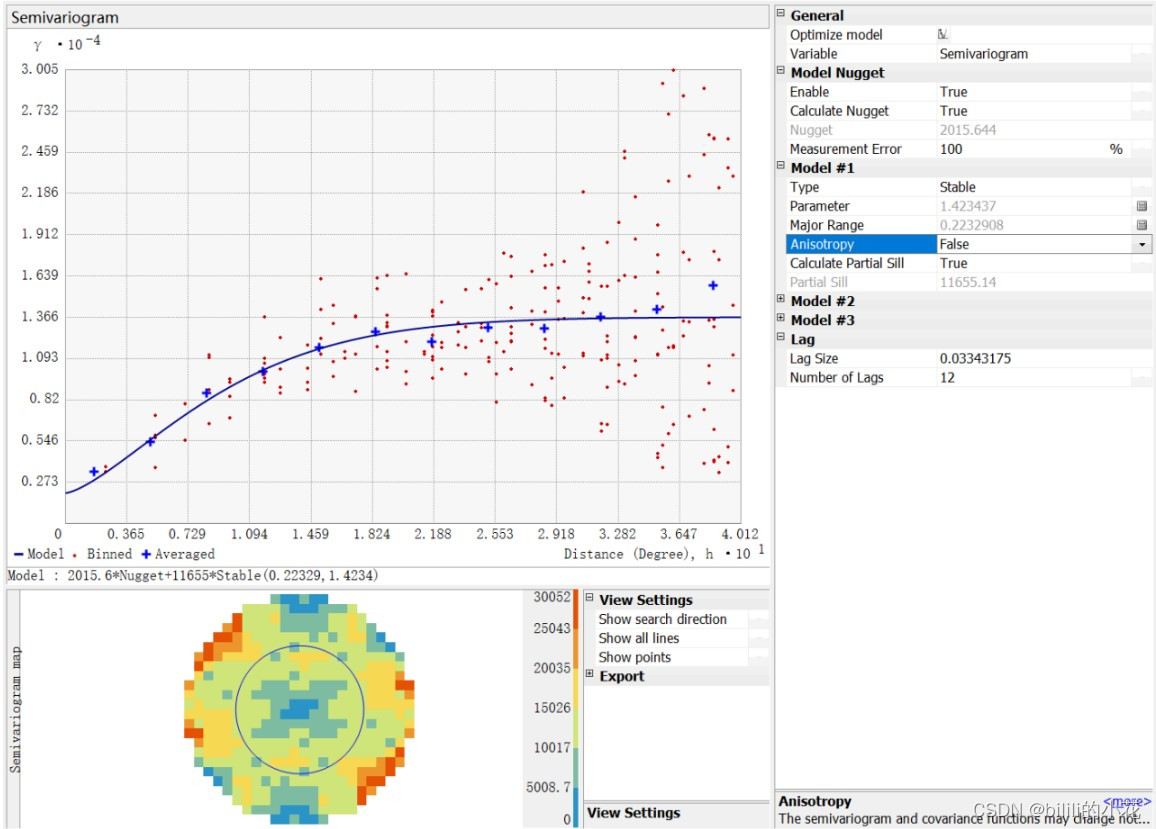
还可以查看不同方向上的半方差情况:

点击下一步,获得普通克里金的模拟结果。
选择上一节的模拟点(103.5,25.35),其模拟值为2165.096,与上一节人工计算出的结果2165.97十分相近,证明了计算方法的准确性。

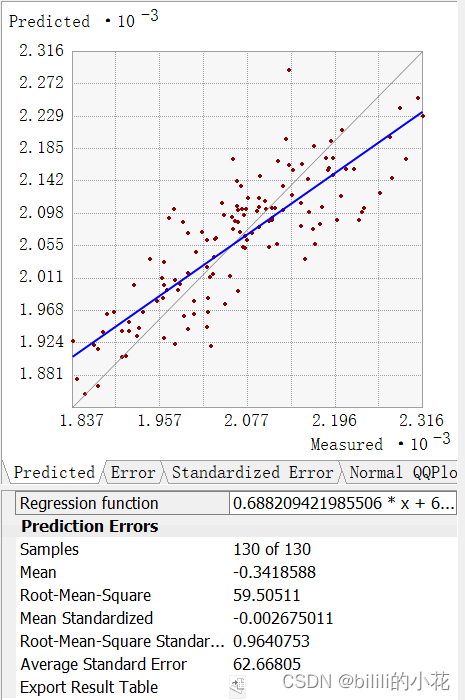
点击下一步,获得模型的相关参数,可用于判断模型拟合度。结果显示,其标准均方根为0.964,平均标准误差为62.668。
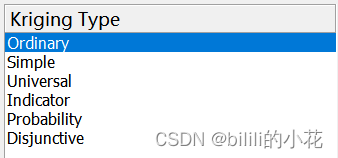
在Geostatistical Analyst中,存在多个可用于表面创建的克里金方法,包含普通克里金、简单克里金、泛克里金、指示克里金、概率克里金和析取克里金,都可以进行尝试计算。
本文参考:
https://xg1990.com/blog/archives/222
https://blog.csdn.net/mengjizhiyou/article/details/134147915
https://blog.csdn.net/zhebushibiaoshifu/article/details/114030470
https://blog.csdn.net/hu397313168/article/details/130697897
如有不足之处,欢迎指出。























 738
738

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








