密钥更短、速度更快--ECC如何重新定义现代加密-CSDN博客

本文链接：https://blog.csdn.net/weixin_43903639/article/details/147897271

在当今的数字世界里，加密算法是保护数据安全的核心。几十年来，RSA（基于大数分解难题）一直是公钥加密的黄金标准。但随着计算能力的提升和量子计算的威胁，RSA 的局限性逐渐显现——它需要很长的密钥（2048位甚至更长）才能保证安全，导致计算开销大、速度慢。

而 椭圆曲线加密（ECC, Elliptic Curve Cryptography） 的出现，彻底改变了这一局面。它能够在更短的密钥长度下提供同等级甚至更高的安全性，同时计算速度更快、资源消耗更低。

一、椭圆曲线

椭圆曲线有多种表达形式

维尔斯特拉斯通用式： $y^2 = x^3 + ax + b$

维尔斯特拉斯一般式： $y^2 + ay= x^3 + bx^2 + cx + d$

勒让德标准式: $y^2 = x(x-1)(x-\lambda)$

这些方程的形式多样，但是都可以通过一定的数学变换转化为常见的维尔斯特拉斯通用式。

为了让椭圆曲线没有奇异点，即处处光滑可导，需要满足其判别式不为零，即 $\Delta = 4a^2 + 27b^2 \neq 0$ 。

判别式的几何意义：

$\Delta > 0$ ：曲线无奇点，且有三个不同的实数根（曲线有两个连通分支）。
$\Delta = 0$ ：曲线有奇点（尖点或自交点），不能用于密码学。
$\Delta < 0$ ：曲线无奇点，但只有一个实数根（曲线是单连通）。

1.1、椭圆曲线的奇点判别

椭圆曲线的奇点是指同时满足以下方程的点 (x,y)：
$\begin{cases} F(x,y) = y^2 - x^3 - ax - b = 0 \\ \frac{\partial F(x,y)}{\partial x} = -3 x^2 - a = 0\\ \frac{\partial F(x,y)}{\partial y} = 2 y = 0\\ \end{cases}$
由 $\frac{\partial F(x,y)}{\partial x} = -3 x^2 - a = 0$ 可得 $x^2 = -a/3$

由 $\frac{\partial F(x,y)}{\partial y} = 2 y = 0\$ 可得 $y = 0$

带入曲线方程 $y^2 = x^3 + ax + b$ ，由 $y = 0$ 可知
$x^3 +ax + b = 0$
带入 $x^2 = -a/3$
$x(x^2+a)+b = 0 \rightarrow \frac{2}{3} ax + b = 0\rightarrow x= -\frac{3b}{2a}$
带入 $x^2 = -\frac{a}{3}$
$\left(-\frac{3b}{2a}\right)^2 = -\frac{a}{3} \rightarrow 4a^2 + 27b^2 = 0$
因此 $\Delta = 4a^2 + 27b^2 = 0$ 时存在奇点。

1.2、阿贝尔群

阿贝尔群主要有五个性质：

封闭性，即群内两数 $a + b$ 的结果仍在群内。
结合律，即 $(a + b) + c = a + (b + c)$
有单位元， $a + 0 = 0 + a = a$ ， $0$ 为单位元
有相反数， $- a$ 存在
交换律， $a + b = b + a$

符合这五点，就是阿贝尔群了。

1.3、射影平面

射影平面是欧几里得平面的一种扩展，它通过引入"无穷远点"的概念，解决了平行线在传统欧几里得几何中没有交点的问题。这种扩展源于对欧几里得第五公设（平行公设）的深入思考。

在射影几何中：

每对平行线都被认为在无穷远处相交于一个唯一的"无穷远点"；
所有无穷远点构成"无穷远直线"；
这个扩展后的平面被称为射影平面，记作 $P^2$ ；
无穷远点通常用符号O（或0）表示，在椭圆曲线密码学中常作为群的单位元。

这种构造使得射影平面具有完美的对称性：任意两条不同的直线必定相交于一点，任意两个不同的点必定确定一条直线。这种性质使得射影几何成为研究曲线和曲面的有力工具，特别是在代数几何和密码学中。

二、椭圆曲线群律

对椭圆曲线群做出如下定义：

单位元就是上文所说的无穷远点0
某点的相反数为该点在椭圆曲线上关于X轴对称的点，即点 $P$ 有相反数 $- P$
随机取椭圆曲线上两点 $P$ 和 $Q$ ，经过这两点的直线与椭圆曲线相交于第三点 $R$ ，这里定义加法规则： $P + Q + R = 0$

这样的一个椭圆曲线群就是阿贝尔群，因为 $P, Q, R$ 并未规定先后顺序，所以
$(P + Q) + R = P + (Q + R) = P + Q + R = P + Q + R + 0 = 0$
满足交换律结合律和封闭性。故为一个阿贝尔群。（这里只是说明，并不严谨）

常见的情况就是这种三个交点的情况：

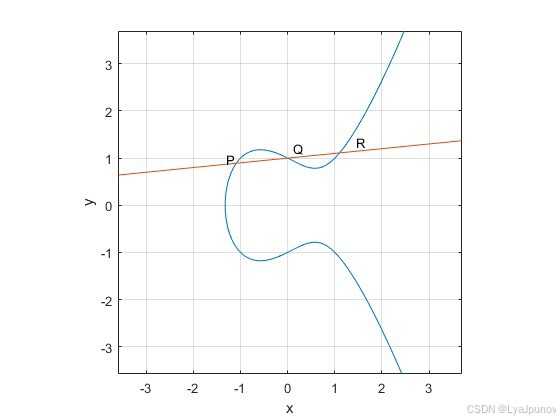
请添加图片描述

但是会不会出现只有两个交点的情况呢，实际上是会的

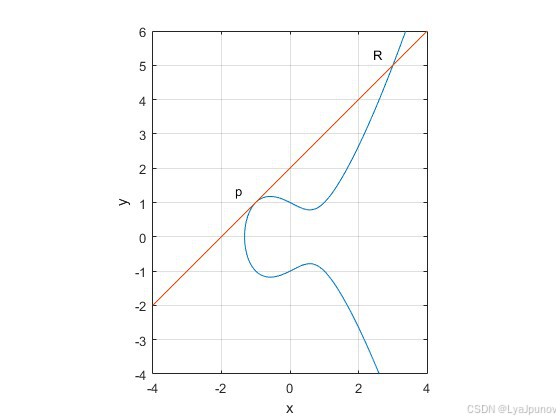
请添加图片描述

这种情况下，加法规则依旧是成立的，只不过形式上变成了 $P + P + R = 0$ ，还有一种情况，就是这条线彻底竖起来了，垂直于X轴，这种情况也是只存在两个交点：

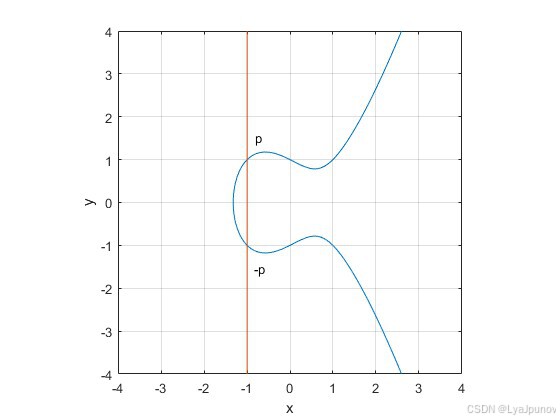
请添加图片描述

这种情况就可以理解为 $P + (- P) + 0 = 0$ ，注意：0 也是无穷远点。

以上就是直线与椭圆曲线之间交点的内容，略显抽象。

三、椭圆曲线加法

前面的那些饺子，都是为了现在的这盘醋，现在，醋来了：

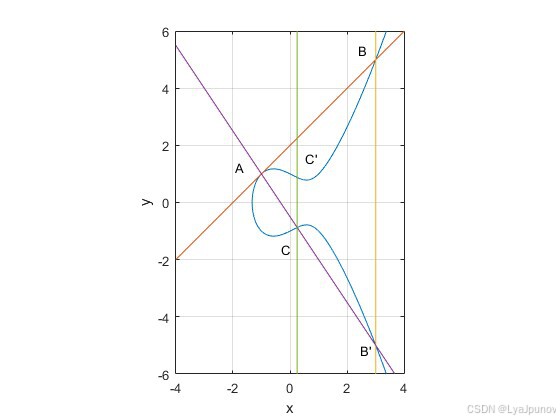
请添加图片描述

首先我们选的点是 A，从 A 可以做椭圆曲线的切线，那么就有等式成立
$\Rightarrow 2A+B = 0 \Rightarrow 2A = -B \Rightarrow 2A = B'$
从 A 到 B’ 还可以连一条线，那么可以得到 C
$\Rightarrow 3A + C = 0 \Rightarrow 3A = C'$
这样可以一直推导下去，A 和 C’ 之间还可以再连线生成 D。可以发现，最终生成的点(带撇的) 只与最初的点A相关，与过程中的B无关。

那么，我们是不是就可以将最初的点 A 当做生成点，多少次这样的过程 k=3 当做私钥，最终点 C’ 当做公钥

这个例子是比较简单的，给人一种好像知道了起始点 A 和最终点 C’ 就可以知道中间连了多少次线 (k) 的错觉，现在告诉你，终点 $C^{'}$ 与 A 的关系如下：
$C^{'} = 115792089237316195423570985008687907853269984665640564039457584007913129639747 A$
你是不是就傻眼了，你一个个试的话是正向推导，从 A 开始，一步一步的试验每一个数最终是否会与 C 相交，时间复杂度相当高。这种逆推导在加密领域也被求解对数问题，时间复杂度也相当高。

那么以上就是椭圆曲线加密的整体概念了，整个加密的过程就是这样的一个方式。

四、椭圆曲线代数运算

我们要把上述抽象的连线转换成代数运算，方便计算

在椭圆曲线上取 $P$ 点 $X_P,Y_P)$ ，在 $P$ 点做椭圆曲线的切线交椭圆曲线上的 $R$ 点 $X_R,Y_R)$ ，切线的斜率为：
$\frac{3 X_P + a}{Y_P}$
设切线
$\frac{3 X_P + a}{Y_P} x + c$
带入椭圆曲线
$y^2 = \left( kx + c \right)^2 = x^3 + ax + b \Rightarrow x^3 -k^2x^2 + (a-2kc)x+b-c^2 = 0$

一元三次方程 $ax^3+bx^2+cx+d=0$ 的三个解有如下关系：

$x_1 + x_2 + x_3 = -\frac{b}{a}$
$x_1 x_2 x_3 = -\frac{d}{a}$
$x_1 x_2 + x_2 x_3 + x_1x_3 = \frac{c}{a}$

将 $X_P+X_P+X_R = -\frac{b}{a}$ 带入可得 $X_R = k^2 - 2 X_p$ ， $Y_R = Y_P + k(X_R-X_P)$

于是可求得 R 点坐标 $X_R, Y_R)$

一般来说，一个正常的加密过程，肯定是反复弹点连线之后才会产生一个结果点，这样通过简单的形式表示就是 $n P = N ’$ 。这一形式被称为标量乘法。在最终取到 $N ’$ 点时，肯定经过了多次的打点，那么 $n$ 就会是一个比较大的数。如果以这样的步骤一个一个的进行点坐标的运算，那和直接破解也没什么区别了。所以这个数就不是可以这么一个一个打点算的，而是使用倍加算法。
$N' = 151 P = 2 ^ 7 P + 2 ^ 4 P + 2 ^ 2 P + 2 ^ 1 P + 2 ^ 0 P$
这样只需要计算7次并相加，而不是151次。

五、有限域上的加法

上述所有的结论都是在连续点和无限域上的，X轴Y轴可以无限向前向后延伸，某段曲线可以无限的细分下去，这符合数学，但是不符合计算机的计算逻辑，计算机无法表示无限的空间延伸，也无法表示无限细分的小数。所以我们要把本来在无限域和连续点上的方法，转化到有限域和离散点上来。好在这个过程比较简单(但是难以理解…)，只需要对所有的数取模，对所有的方程取模即可。

负数取模： $\ mod \ m = a - m \lfloor \frac{a}{m} \rfloor$ （ $\lfloor \rfloor$ 是向下取整的意思，负数就是负无穷方向）

举个例子： $\ mod \ 3 = - 7 - 3 \lfloor\frac{-7}{3}\rfloor = - 7 - 3(-3) = -7 + 9 = 2$

倒数取模：是指对于一个整数 a 和模数 m，找到一个整数 x，使得 $\equiv 1(mod \ m)$ 此时，x 称为 a 在模 m下的乘法逆元，记作 $a^{−1} \ mod \ m$ 。

计算步骤：

计算 gcd⁡(a,m)，如果 ≠1，则逆元不存在。
回代求解 x 使得 ax≡1(mod m)。

**示例：**计算 $3^{-1} \ mod 7$

计算 gcd⁡(3,7)=1，逆元存在。
$\equiv 15 \equiv 1(\ mod \ 7)$

matlab代码：
a = 3;
m = 11;
inv_3 = powermod(a, -1, m); % 计算 3^(-1) mod 11
disp(inv_3); % 输出 4

在无限域中的代数运算方程，在有限域中也可以使用，只不过是在计算结果上加个 $\ p$ 。

交点的运算坐标可得 $X_R = (k^2 - 2 X_p) \ mod \ p$ ， $Y_R = (Y_P + k(X_R-X_P)) \ mod \ p$ ，斜率 $\frac{3 X_P + a}{Y_P} \ mod \ p$

如果你把斜率的模运算(有限域)和非模运算(无限域)对比，会发现它们给出的结果完全不同。

比如曲线 $y^2 = x^3 + 7$ 这条椭圆曲线，在 $\sqrt{34})$ 点的斜率存在，但是这个点在有限域中的点 $(3, 0)$ 在这点的斜率是无穷大，虽然运算产生的结果不同，但他们各自的结果确实在他们各自的域内能完美的接洽逻辑。当然，上面只是给出了个例子，要真正证明这一群律在不同的域内都适用，需要严格的数学证明，这里不在给出。