瞬时功率

image.png
根据乘积化加减 它有两种分解方法:
第一种

image.png
前面拆成一个常数 后面是一个随t变化的函数 但是这种做法 拆出来的两项没有具体的物理意义 唯一一点的好处就是 好积分 求平均功率的时候好算
第二种分解方法:
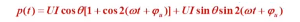
image.png
我们拆成一个 有加常数C的 一个没有加的随t变化的三角函数

image.png
这个就有具体的物理意义了 可以画出图

image.png

image.png
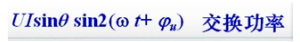
image.png
因为它的平均值为0 所以不消耗功率 只交换功率
上面的是瞬时功率

瞬时功率的两项
第二项是由t决定 平均为0的 它的系数就称为无功功率Q

其实它和功率因数很相似
无功功率和平均功率 看起来 就是一个 直角三角形(或者说相量)生的一样 不过一个取实部 一个取虚部
而这个直角三角形 就是视在功率 实实在在看得到的 有效的 功率

接下来讲 平均功率 平均功率 就是一个周期内的平均的功率
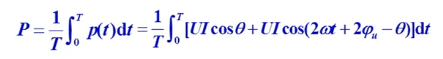
image.png
算出来的结果就是

image.png
然后在这个式子中 我们又有了一些新的概念

功率因数
简单理解 其实 就是对阻抗角取个余弦值
功率因数角就是

功率因数角
功率因数分析

image.png
功率因数求法:其实可以用 阻抗的虚部比实部的正切值tan 来求出角度
感性与容性
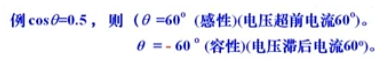
交流直流的区别
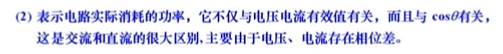







 本文深入探讨了瞬时功率的两种分解方法及其物理意义,分析了无功功率的概念,并详细解释了平均功率的计算方式及功率因数的含义。
本文深入探讨了瞬时功率的两种分解方法及其物理意义,分析了无功功率的概念,并详细解释了平均功率的计算方式及功率因数的含义。
















 930
930

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








