目录结构
注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下:
1、参考书籍:《算法导论》第三版 就是这本被封神的杰作,就是它🤦
2、参考书籍:《数据结构》严奶奶版
3、参考书籍:《数据结构》(用面向对象方法与C++语言描述) 第二版 殷人昆版
4、散列表的基本概念及其运算,点击前往
5、hash算法原理详解,点击前往
6、哈希表(散列表)原理详解,点击前往
7、散列表,点击前往
8、参考书籍:《数据结构》(C++版) 第三版 邓俊辉版
9、哈希表(散列表)原理详解,点击前往
10、麻省理工学院 算法导论公开课,点击前往
11、《算法导论》读书笔记之第11章 散列表,点击前往
DSA 经典数据结构与算法 散列

文章快速说明索引
学习目标:
前言:还记得在大学的时候,数据结构作为计算机科学与技术专业最重要的一门课 当时学校采用的教材是严奶奶的粉红色那本,不过当时是真的不愿多看一眼 😂 苦涩难懂 又非常深奥,满篇伪代码实现的例子和夏日那十分惬意的下午 简直让人头大而晕!
也可能是上学那会儿年少浮躁,也可能是因为当时的能力比较的菜吧 ┑( ̄Д  ̄)┍ 。现在再回头捧读厚厚的《算法导论》,竟然有一种说不上来的快乐 沉浸在数据结构和算法之美,惊叹于高超技巧式拍案惊奇 再加上最近的工作中需要HASH的支持,故而再回顾回顾 竞技之枪-散列 的强大之处 权做是弥补一下当年偷下的懒!
学习内容:(详见目录)
1、数据结构与算法(DSA)之散列
学习时间:
2021年01月23日 04:30:39 - 2021年01月31日 23:29:31
学习产出:
1、CSDN 技术博客 1篇
2、PostgreSQL数据库 基于HASH的模块的参数调整
注:本文内容来源于以上书籍和网站,以及个人对于HASH的理解。不保证完全的准确性,有问题或疑问 请在评论区留言 Thinks o(* ̄▽ ̄*)ブ

散列表的背景介绍
散列:是一种极其有效和实用的技术。基本的字典操作平均只需要O(1)的时间。
散列表 又称哈希表(Hash Table),是一种实现了 字典操作 的高效算法基础,是一种根据关键字码值(K-V对) 直接进行访问的数据结构。
关键信息 :
1、是一种支持
Insert Search Delete等字典操作的动态集合结构
2、通过将关键码值映射到表中一个位置来访问记录,以得到快速查找的最佳性能(通常平均情况下,查找元素的时间复杂度为O(1)) 即使在最糟糕的情形下:哈希表中Search某记录的时间也与链表下一致 达到O(n)
3、上面所说的关键字码值的意思:散列表(数组)的下标并不是直接使用关键字(也可以用),而是使用 根据关键字计算出来的值
4、作为普通数组的延申:因为对普通数组可以做到 直接寻址,即在O(1)的时间内访问数组中的任意位置。于是在空间使用允许的情况下 我们可以直接使用 直接寻址技术的优势:提供一个为每个可能的关键字保留一个位置的足够大的数组
上面所说的足够大数组指的是:实际上需要存储的 Key 数目比所有可能的关键字总数小时,此时的散列表成了 直接数组寻址 的有效实现。具体的做法就是:Hash表使用一个 长度length和实际存储的关键字数目成比例的 数组 来存储。
接下来我们的Hash学习将着重聚焦于以下概念的展开和问题的解决:
1、直接寻址法及其缺陷
2、Hash函数的使用和哈希冲突
3、链式地址法 开放寻址法
4、完全散列
散列表的实现技术
直接寻址法及不足
在开始之前,需要设计如下的技术背景:
1、所有可能的关键字的集合 记为U={0,1,2,…,n-1} ,每一个关键字将是其中之一
2、关键字间彼此 不重复
3、n 即 可能性的总数,该值不是很大。即:关键字U域就比较小
在上面的场景下,直接寻址法是一个非常高效而又简单的技术。详细如下:

1、如上
T[0,...,n-1]是一个对应所有关键字集合的 数组(表示这个动态集合),也被称之为 直接寻址表
2、n 值不大,因此该数组T 所占用空间可以接受,此时该数值与U域 的总数保持一致
3、关键字集合 K域 中的每个Key,与直接寻址表里面每一个 槽号 一一对应。对应该槽中存储的将是该关键字映射的数据的指针ptr,后面卫星数据将存放 真正有意义的数据元素
4、K域以外的关键字 或者说 T[]中没有对应到的槽 将是T[k]=nullptr的状态
有了这样的结构,其Insert Search Delete等字典操作将变的非常高效:
DR_search(T,k)
{
return T[k];
}
DR_insert(T,x)
{
T[x->k]=x;
}
DR_delete(T,x)
{
T[x->k]=nullptr;
}
// 显而易见 上面字典操作都可以在O(1)的时间复杂度下完成
上面伪码展示是直接寻址法的一种实现,在实际使用中 可能要存储的有效数据本身并不复杂 就可以直接存储在直接寻址表(数组)里面。
1、直接寻址表作为数组 本身即可存放 动态集合中 的数据
2、要存储的数据相对简单的时候 可以直接存放在表的槽中,无需使用上面复杂的 指针ptr指向表的外部对象的操作。可是若是一个较为复杂的数据,例如一个较大空间占用的对象呢 (总之,这个具体情况具体分析)
3、倘若是直接将对象存储在表中的话(不使用ptr进行指向),那如何来判断该槽是否为空呢?办法之一:使用对象内 某一特殊关键字 来表明是否为空。此外,也不需要去存储该对象的关键字Key的信息 因为若是知道该对象在表中的下标,就可以得到其关键字。但是这样的话 就必须要某种方法来验证某个槽是否为空
上面第三点,有些绕 我个人的理解如下(设计如下场景案例)
1、假如上面图中的卫星数据是 这样的两位数:
23 32 56 88(当然不会重复且每十位上只有它一个)
2、这样的话 直接存储对象(不用指针)且省去其关键字信息的情况下,T[]里面可以直接存储23 32 56 88
3、确定对象关键字的方法可以是:value / 10操作(这也是存储位置的依据);确定某一个槽是否为空的方法:预置T[]里面 全为 -1,然后校验其中是否为 -1
如上就是直接寻址法的技术说明,但是它在如下场景下是不堪一击 或者 难堪大用的:
- 全域U的范围 n 非常之大,这样的T[] 所需要的空间 在系统中,无法接受
- 实际存储的 K域 相较于整个的 U域 又十分的小的话,T[] 大部分空间白白浪费
哈希函数下的冲突
在上面直接寻址法的不足中,其硬伤在于:空间的使用上(或利用率)。我们设想一下:在 K域 相较于一个很大的 U域 的情况下,大量的空间(分配给T[]的)被白白浪费。假设K域的个数为 m,U域的个数为 n。
m在n的占比不高,其实我们所需的存储空间也就是一个 m 而已(即:空间存储需求为O(|K|)),但是又要兼顾到 哈希表的Search 效率仍为O(1),此时散列的方式应用而生!
上面也说了 在直接寻址法下,具有关键字k的元素被存放于 槽k T[k]里面;在散列的方式下,具有关键字k的元素将被存放于hash(k)中。(hash()是散列函数,通过关键字k来计算该元素的存放位置)
1、散列函数
hash()的存在 将关键字的全域 U域 映射到散列表T[]上面,且此时的T 范围是[0,1,2...,m-1]。这里的m将是一个可以接受的空间值 如下图所示
2、优势在于:散列函数 缩小了数组T的下标范围 大大地减少了数组的大小 由原来的|U|减至 m,它比|U|小的多
3、接下来就是 每一个具有关键字 k 的元素通过hash()被散列到槽hash(k)里面,这时 我们也可以说hash(k)是关键字 k 的哈希值
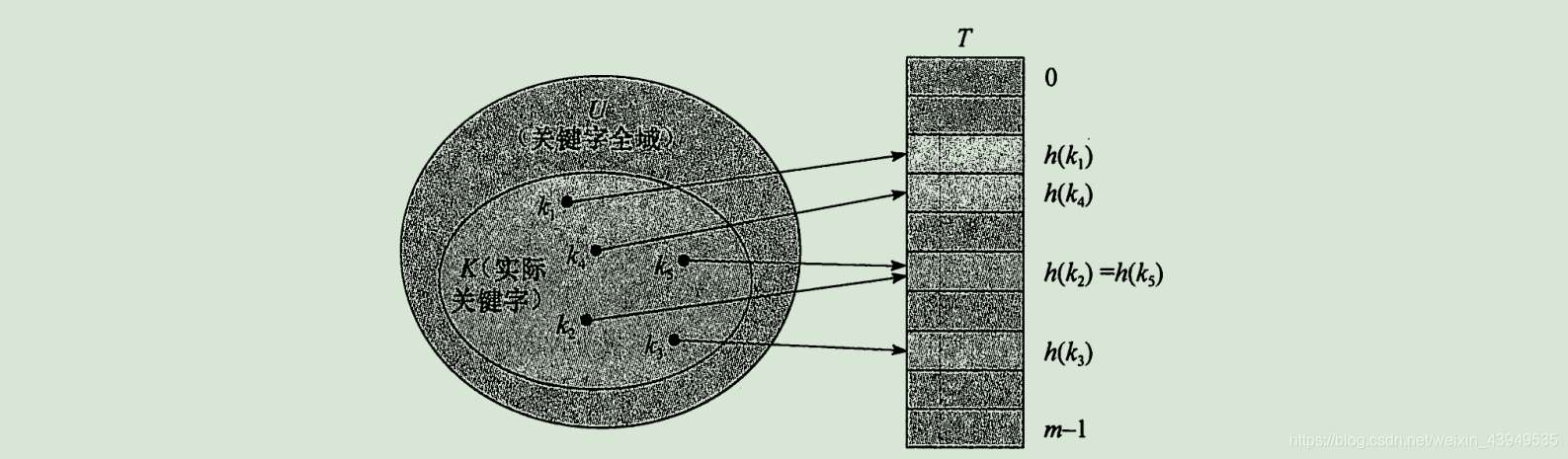
但是这样子会有一个问题,还是上面的案例 假如卫星数据是 这样的两位数:23 32 56 88 ,且哈希函数 hash(k)=k%5:
1、计算上面四个数的哈希值:
3 2 1 3有相同的
2、就如上图所示的 关键字 k2 k5的哈希结果一样,它俩被映射到同一个槽中 我们称这种情况为 哈希冲突 (多个关键字被映射到数组的同一个下标里面)
为什么会产生哈希冲突,以及如何避免和解决哈希冲突呢?
1、哈希(散列) 就是 随机混杂和拼凑的意思
2、鉴于哈希函数必须是确定的 确定指的是:对应给定的输入key,始终都应该产生相同的 哈希结果值。但是因为|U|的规模远大于 m,所以完全避免 哈希冲突 是不现实的
3、对于哈希冲突 我们一方面可以通过精心设计的hash()来尽可能的减少冲突;另一方面,需要解决冲突的方法
上面也说到了,虽然可以 选择一个精心设计的哈希函数 来做到避免(而非完全避免)所有的冲突。那么这个函数就需要做到一点:尽可能的 随机 !
除了这种治标不治本的办法外,下面也将会介绍几种解决哈希冲突的办法:
- 链式地址法
- 开放寻址法
设计好的哈希函数
上面也说了 好的哈希函数即使设计的很完美,也不可能根治哈希冲突 顶多就是可以做到尽可能的减少或避免冲突的发生。下面将介绍一下 如何设计一个优秀的散列函数:
- 启发式方法:设计过程中利用 关键字分布 的有用信息
- 除法散列
- 乘法散列
- 利用随机技术
- 全域散列
那么首先看一下好的哈希函数拥有哪些好的品质:
应该(近似的)满足 简单均匀散列 :
1、每个关键字都被等可能地散列到 m 个槽中的任何一个,且与别的关键字 映射到哪个槽位 无关 1
2、若是知道关键字的概率分布,例如:各个关键字都是 随机的 且 独立均匀分布在[0,1)中的实数k,此时设计哈希函数为:hash(k)=floor(k*m)即可满足 简单均匀散列 的假设条件
3、对于启发式方法设计的函数:应尽可能将 相似关键字 给散列到不同的槽中;经过哈希之后的散列值 在某种程度上应该独立于数据可能存在的任何模式
4、哈希函数的某些应用可能会要求比 简单均匀散列 更强的性质。例如:可能希望在某些很相近的关键字间具有截然不同的散列值
5、下面的全域散列 通常可以提供以上性质
注:这里需要声明一下,暂时考虑的关键字都是自然数。倘若不是自然是呢?例如关键字是字符串,key="pt"。这样的情况下就需要使用某种规则将其转化为一个自然数 示例如下:
// key="pt"
1. 转化为十进制整数对 (112,116) 这两个数是对应的ASCII码
2. 以128为基数
3. 计算 transf(key)=112*128+116=14452
除数散列法
对于key是整数的情况,常用的哈希函数有如下:
- 直接定址法:恒等变换
hash(key)=key直接把key作为数组下标;或是 线性变换hash(key)=a*key + b - 平方取中法:指得到 key 的平方的中间某几位作为哈希值
- 除数散列法:常用 如下
这个应该是我们在使用哈希函数最常用的技术:通过得到 k%m 来取余,将关键字k映射到 m 个槽中的某一个位置。该散列函数为:
hash(k)=k%m;
// 只需要做一次除法操作 效率非常快
这里需要注意一下 基值m 的选取:
1、不要选 2的幂
2、建议选取一个 不太接近2的整数幂 的素数
上面为什么这么说呢?下面举个例子进行说明:
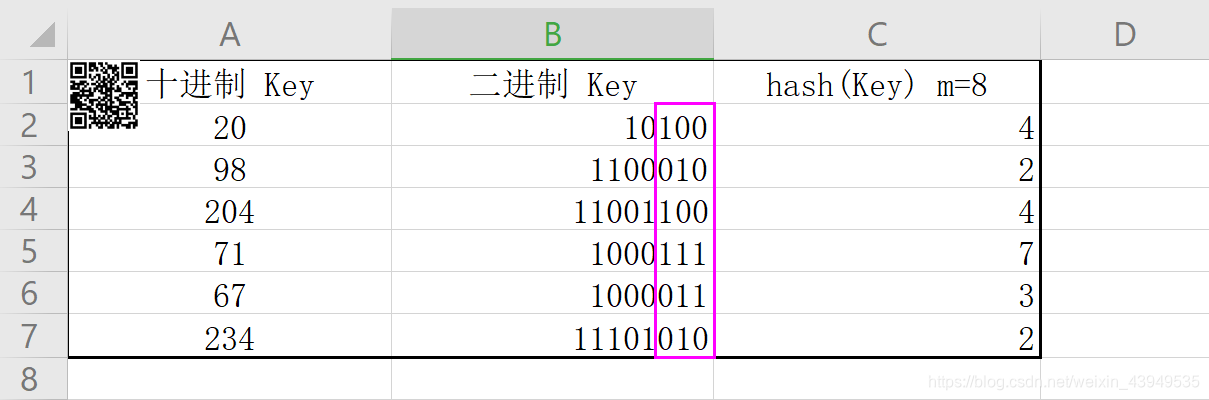
m=8=2*2*2
p=3
如上 hash()的结果 变成了 低p位的数字,除非已知各种最低p位的排序形式 为等可能 否则在设计哈希函数的时候,最好要考虑到关键字的所有位。从概率的角度,出现相同的概率比较高,而 通常我们希望 hash(k) 的值依赖于 k 的所有位而不是最低 p 位,因为这样才会使得散列表看起来更均匀。当m不是素数时在散列分布时也会增加分布不均匀的机会,总的来说哈希函数的设计尽量使键值均匀、随机地分布在表中。
m=2p−1也是一个糟糕的选择,因为排列 k 的各字符不会改其散列值(下面有示例证明)。书中最后也提到了一个例题:

其定理证明如下:

注:上面这个英文 能看懂可以看看,看不懂就算了 下面有个例子可以帮助理解!
对于不同的字符串S1 = “abcd” S2 = "adcb",它们的hash值是相同的 但是它们是不同的字符串,他们会冲突!考虑字符串中的单个字符的顺序,对各个字符串进行加权,而加权的具体方式就是他们所处于字符串中的位。示例如下:
上面题中说的那句
k为按基数2^p 表示的字符串,可以如下理解
S1 求值可以这样
'a'*2^(0) + 'b'* (2^1) + 'c' * (2^2) + 'd' * (2^3)
S2 求值可以这样'a'*2^(0) + 'd'* (2^1) + 'c' * (2^2) + 'b' * (2^3)
这样两个的字面值就不一样了,真的吗?但是他们的哈希结果还是一样的,下面是本人的个人理解:
而一个不太接近2的整数幂的 素数,往往是 m 的较优选择。书上给了一个简单的例子:
1、例如我们将要存储
n=2000个字符串,其中每个字符有8位
2、使用除法散列法函数 + 链式地址法
3、我们不介意一次不成功我们平均检查3个元素,这样我们分配散列表的大小m为701
因为701是一个接近2000/3,但又不接近任何2的任何次幂的素数
乘数散列法
乘数散列法创建的哈希函数,包含如下两个步骤:
1、使用关键字 k 乘上常数A 范围是(0,1),以得到乘积的小数部分 作为值C 就是下图的()部分
2、使用m乘上C,并向下取整
于是该散列函数为:
不知道这个公式是来干啥的,《算法导论》在这里提了一下 就没有然后了。这一点让我很痛苦: 为啥 凭啥 干啥
注:在学习《算法导论》的时候,会经常性的傻掉。为什么呢?
1、《算法导论》内容实在是太过苦涩 语言描述和翻译都不好我感觉
2、外国人的脑回路 可能跟我们不太一样
3、好好的句子 读着读着变味了,不知道在说啥 前后联系不起来
乘数散列法 这块内容我真的有些迷惑,此点症结在于:
1、下面的示例和乘数散列法讲解 跟上图的公式脱节了 不知道上面公式在干嘛
2、下面的示例中的数据 使用上面公式算出来的不一样,它是来搞笑的吗
3、接下来的讲解 苦涩难懂 有知道上面疑问的小伙伴请把自己的理解 打到评论区
头脑风暴开始 :一种让人理解不了的哈希计算方式,门槛过高
乘法散列的一个优点是对 m 的选择不是特别的关键,一般选择它为 2 的某个幂次(m=2p ,p 为某个整数),这样可能正好使用计算机的一个字长(这样我们可以在大多数计算机上,使用下面的方法来轻易实现哈希函数)。假设计算机的字长为w位,而k正好可以用一个单字表示。限制A为形如 s/2w 的一个分数(其范围是 0<A<1 ),其中s是一个取自 0<s<2w 的整数。如下图所示:

先用w位整数 s=A * 2w 乘以k,其结果是一个2w位的值 r1*2w + r0,这里r1为乘积的高位字,r0为乘积的低位字。然后所求的p位散列值中,包含了r0的p个最高有效位。在实际使用中 A值的选取 会影响到散列的实际效果,目前被认为最优的A值 是 黄金分割比 0.618:
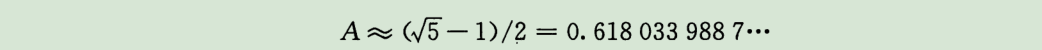
关于黄金分割比 还有一个有趣的小故事,可以参考 这位大佬的博客:八卦中不可思议的数字规律,点击前往

OK 废话不多说,下面是本书提供的一个示例(高深莫测):
1、要利用黄金分割比 (sqrt(5) - 1) / 2 = 0.6180339887…
2、k=123456, p=14, m=214 =16384
3、w=32
4、取A为形如s/232 的分数,它与(sqrt(5)-1)最接近,于是A=2654435769 / 232
5、于是上面 s=2654435769
那么 k * s = 327706022297664 = (76300 * 232 ) + 17612864,于是就有了 r1 =76300 和 r0 =17612864的结果
r0=17612864
二进制:1 0000 1100 1100 0000 0100 0000
取最高14位:0000 0001 0000 11
于是 r0的前 p=14 位最高有效位产生的散列值就是 hash(k) = 67
OK ,那么上面说的这些 和上面列举的公式有什么关系?
全域散列法
背景:对于任何一个即使经过优秀设计的哈希函数而言,都无法保证 n个精心挑选的关键字集合 不会被映射进同一个槽中的可能。若是一旦被恶意者获取到该散列函数的信息,哈希函数hash()将不再拥有优异的性能,此时的平均下的查找时间也都会是O(n)级。
针对这种情况,为了保证 平均性能 唯一有效的做法就是:设计一组优异的函数,在全域散列法开始执行时 随机地选取散列函数 使哈希的结果独立于要存储的关键字。 但是需要注意的是:不是说每次操作都选择一个哈希函数,而是构建一个哈希表的时候随机选一个,选定之后这个哈希表的所有操作都是基于这个哈希函数(这个函数是不变的),这种方法可以有效地防止 精心设计一个关键字集合击溃哈希表的可能,同时也能避免某些集合永远会导致较差的性能。倘若真的是,那么重新建一个散列表即可。
这种方法被称之为 全域散列法,这样无论关键字将怎么特殊 或 任何输入 查找的平均性能都很好。这一点类似于 快速排序,随机化保证了没有哪一组输入会始终导致最坏的情况出现。
但是需要注意的点如下:
1、因为是随机的从一组哈希函数中挑选一个,算法在每一次执行的时候都会有所不同 即使是面对相同的输入
2、仅当应用选择了一个随机的哈希函数,且它使得关键字的散列效果较差时 才会出现较差的性能。但是这一概率较低
一个函数组被称为 全域的,其相关概念如下:
1、U是关键字key的全域
2、HSet是一组哈希函数的有限集合,每一个都是将U映射到 散列表 的m个槽{0,1,..,m-1}中
3、如果对所有不等的两个关键字k,l ∈ U,集合{ h | h ∈ HSet && h(k) = h(l) }的元素个数最多等于|HSet|/m,则称 HSet 为 全域哈希 。即将集合HSet划分为m份,对于任何两个不相等的key,只有1份包含的hash函数是会使得两者的hash值相等
4、第3条 也可以这么理解:如果从集合HSet中 随机选取一个哈希函数,当关键字k l不相等的时候 两者的哈希结果发生冲突的概率 不高于 1/m。而这也正好是从 m个槽{0,1,..,m-1}中 独立随机选择hash(l) hash(k),发生冲突的概率

下面书上给了一个关于 全域散列法的平均性能优异的定理,其中
n
i
n_ {i}
ni 是链表 T[i]的长度:

书上也给了它的详细证明,不过 可能是翻译的锅吧。明明可以好好说的话,偏偏拧着说 理解起来费时费力还影响心情 唉,下面是个人的理解:

上面就是 对于一个关键字 k,与k产生冲突的关键字的数量的期望值。全域散列法在随机化下可以达到哈希的理想效果!同时书上提供了如下的推论:
对于一个具有 m 个槽位且初始时为空的表,利用全域散列法和链式地址法解决冲突 需要O(n)的期望时间来处理 任何包含了 n个 Insert Search 和 Delete的操作序列,其中该序列包含O(m)个Insert操作
证明 :
1、Insert 和 Delete操作为常量操作
2、Insert操作的数目为 O(m),所以 n=O(m) 装载因子 a=O(1) 由上面的定理可得:每个Search的期望时间为O(1)
3、根据期望的线性性质可得:每个操作所用的时间都是常量,整个n个操作序列的期望时间为 O(n)
综上所述:全域散列法可以达到期望的效果:无法通过一组特殊输入来使得达到最坏情况的运行时间,在运行的时候 随机选择散列函数,即可确保每个输入都具有良好的平均情况运行时间。
至于怎么设计 一个全域散列函数类:(需要涉及到 数论 的知识范畴)
1、选择一个足够大的素数p, 使得每一个可能的关键字k都落在[0,p-1]的范围内
2、设Zp 表示集合{0,1,....,p-1},Zp* 表示集合{1,2,....p-1}。由于p是一个素数,且因为我们假设 关键字的全域大小大于散列表中的槽数,故有p>m
3、现在,对于任何a属于Zp* 和 任何b属于Zp ,定义散列函数hab, 利用一次线性变换,在进行模p 和 模m的规约,有hab(k) = ((ak+b) mod p) mod m
4、这样得到到散列函数构成的函数簇为 H ={hab :a∈ Zp* , b ∈ Zp }
例如如果有 p=17, m=6, 则 h3,4(8) = 5。每一个散列函数 hab 都将 Zp 映射到 Zm。这一类散列函数具有一个良好的性质:输出范围的大小m 是任意的,不必是一个素数。此外 对于a而言有p-1种 选择;对于b而言有p种 选择 所以函数簇中包含了 p(p-1)个散列函数。
解决哈希冲突方法
链式地址法
其具体做法就是:经过哈希函数映射之后被散列到同一个槽里面的所有元素 串成一个链表来存储,如下图所示:
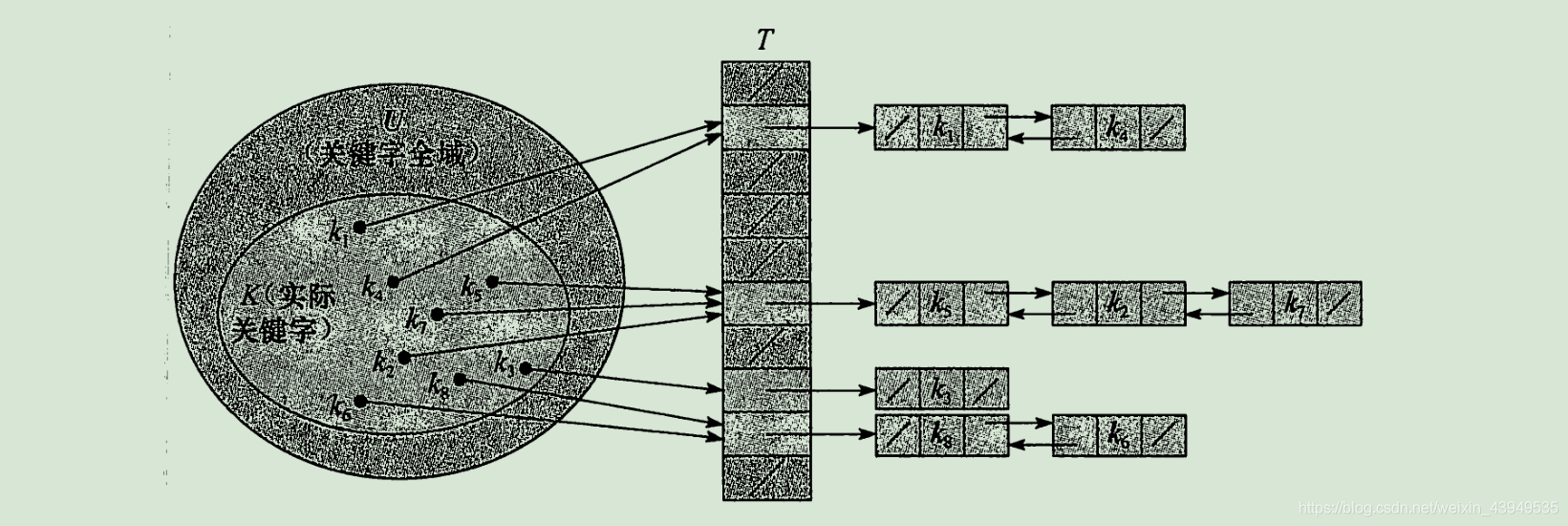
槽k里面的指针指向 存储被散列映射到k的 元素链表 的表头(这个链表里面的元素的 关键字哈希结果一样);若是不存在这样的元素,则该槽k里面为nullptr
那么这样的结构下,散列表T[]的字典操作如下:
HASH_search(T,k)
{
// 在T[hash(k)] 里面寻找键为 k 的
// 最坏情况下 时间复杂度与表长成正比
}
HASH_insert(T,x)
{
// 在T[hash(x->k)]插入x 头插法
// 最坏情况下 时间复杂度也是O(1)
}
HASH_delete(T,x)
{
// 在T[hash(x->k)]删除x
// 元素链表为双向链表,且函数输入为元素x 而非k(这样不需要去搜索x) 最坏情况下 时间复杂度也是O(1)
// 元素链表为单向链表,且函数输入为元素x 而非k(这样需要去搜索x的前驱节点) 最坏情况下 时间复杂度与表长成正比
}
下面来着重看一下 链式地址法的关键字查找效率,背景如下:
1、散列表T[m] m个槽位
2、存放了 n个元素
3、散列表的装载因子为α=n/m代表一条链表的平均储存元素个数
α 的取值为
<1 =1 >1
至于上面所说的 HASH_search(T,k) 最坏情况下 时间复杂度与表长成正比,指的是:n个元素被映射到了同一个链表中,链表长度为n。此时再进行查找,其效率上和一个普通的链表相差无几!
散列方法的平均性能取决于所选择的哈希函数,因为一个好的哈希函数决定了将所有的关键字集合均匀分布在 m 个槽位上的程度。对于哈希函数的讨论,参照上面。接下来先假定一下如下分布:任意一个给定的元素等可能地被映射到 m的槽位中的任何一个,且跟别的元素被映射到什么位置无关。该假设被称之为 简单均匀散列,其数据表示如下:
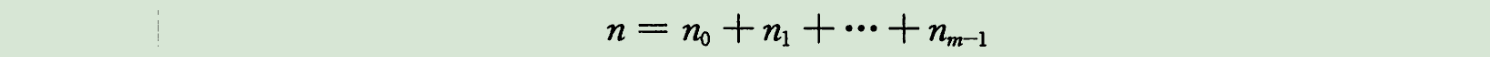
对于j=0,1,...,m-1 ,T[j] 指向的链表的长度 依次为N0 N1 N2 ... Nm-1,其总和为n。并且 nj 的期望值是E[nj]=α=n/m。于是查找一个关键字k的时间 与 对应T[hash(k)]的链表长度成正相关,查找元素的期望 n/m 就是所需要进行比较操作(检查关键字是否为k)的元素数。
对于HASH_search(T,k) 而言,关键字的比对 无非找到或者找不到之分。下面直接给到两个定理而不做详细推理(详细推理见《算法导论》第十一章):
1、在简单均匀散列的情况下 对于使用链式地址法解决哈希冲突的散列表,一次不成功查找的平均时间为 O(1+n/m)
其实这个非常好理解:所有关键字k被等可能散列到m个槽中的任何一个,计算一次哈希的时间O(1)。不成功说明 在
hash(k)的链表中 找到尾部也没有找到 在这里面的查找元素个数 期望为α=n/m。一次不成功的查找意味着 平均要去检查 α 个元素
2、在简单均匀散列的情况下 对于使用链式地址法解决哈希冲突的散列表,一次成功查找的平均时间为 O(1+n/m)
这种情况的理解为:所有关键字k被等可能散列到m个槽中的任何一个,计算一次哈希的时间O(1)。成功 说明在
hash(k)的链表中 找到了,但是 每个链表中并不是等可能地被查找到 ,进行比较操作的元素数 是和 该链表包含的总个数成正比
上面两点说的意思就是:如果散列表中槽数 m 和 表中元素个数成正比的时候,n=O(m) α=n/m=O(1) 也即:查找操作 平均时间 为一个常数。
汇总上面可得:当链表结构是双向链表的时候,插入 删除在最差情况下的时间复杂度是O(1);而查询是在 平均情况下 时间复杂度为O(1)
关于链式地址法,这里有一篇写的非常好的老哥的博客:《算法导论》读书笔记之第11章 散列表,点击前往 大家可以去看一下。下面是文章的一个实例(基于C++模板实现的链式地址法):
其源代码为:
/**══════════════════════════════════╗
*作 者:songbaobao ║
*职 业:我以我血荐轩辕 ║
*CSND地址:https://blog.csdn.net/weixin_43949535 ║
**GitHub :https://github.com/TsinghuaLucky912/My_own_C-_study_and_blog║
**GitEE :https://gitee.com/lucky912_admin/code-up_-pat ║
*═══════════════════════════════════╣
*创建时间:
*功能描述:
*
*
*═══════════════════════════════════╣
*结束时间:
*═══════════════════════════════════╝
// .-~~~~~~~~~-._ _.-~~~~~~~~~-.
// __.' ~. .~ `.__
// .'// 西南\./联大 \\`.
// .'// | \\`.
// .'// .-~"""""""~~~~-._ | _,-~~~~"""""""~-. \\`.
// .'//.-" `-. | .-' "-.\\`.
// .'//______.============-.. \ | / ..-============.______\\`.
//.'______________________________\|/______________________________`.
*/
#include <iostream>
#include <vector>
#include <list>
#include <string>
#include <cstdlib>
#include <cmath>
#include <algorithm>
using namespace std;
int nextPrime(const int n);
template <class T>
class HashTable
{
public:
HashTable(int size = 101);
int insert(const T& x);
int remove(const T& x);
int contains(const T& x);
void make_empty();
void display()const;
private:
vector<list<T> > lists;
int currentSize;
int hash(const string& key);
int myhash(const T& x);
void rehash();
};
template <class T> HashTable<T>::HashTable(int size)
{
lists = vector<list<T> >(size);
currentSize = 0;
}
template <class T> int HashTable<T>::hash(const string& key)
{
int hashVal = 0;
int tableSize = lists.size();
for(int i=0;i<key.length();i++)
hashVal = 37*hashVal+key[i];
hashVal %= tableSize;
if(hashVal < 0)
hashVal += tableSize;
return hashVal;
}
template <class T> int HashTable<T>:: myhash(const T& x)
{
string key = x.getName();
return hash(key);
}
template <class T> int HashTable<T>::insert(const T& x)
{
list<T> &whichlist = lists[myhash(x)];
if(find(whichlist.begin(),whichlist.end(),x) != whichlist.end())
return 0;
whichlist.push_back(x);
currentSize = currentSize + 1;
if(currentSize > lists.size())
rehash();
return 1;
}
template <class T> int HashTable<T>::remove(const T& x)
{
typename std::list<T>::iterator iter;
list<T> &whichlist = lists[myhash(x)];
iter = find(whichlist.begin(),whichlist.end(),x);
if( iter != whichlist.end())
{
whichlist.erase(iter);
currentSize--;
return 1;
}
return 0;
}
template <class T> int HashTable<T>::contains(const T& x)
{
list<T> whichlist;
typename std::list<T>::iterator iter;
whichlist = lists[myhash(x)];
iter = find(whichlist.begin(),whichlist.end(),x);
if( iter != whichlist.end())
return 1;
return 0;
}
template <class T> void HashTable<T>::make_empty()
{
for(int i=0;i<lists.size();i++)
lists[i].clear();
currentSize = 0;
return 0;
}
template <class T> void HashTable<T>::rehash()
{
vector<list<T> > oldLists = lists;
lists.resize(nextPrime(2*lists.size()));
for(int i=0;i<lists.size();i++)
lists[i].clear();
currentSize = 0;
for(int i=0;i<oldLists.size();i++)
{
typename std::list<T>::iterator iter = oldLists[i].begin();
while(iter != oldLists[i].end())
insert(*iter++);
}
}
template <class T>
void HashTable<T>::display()const
{
for(int i=0;i<lists.size();i++)
{
cout<<i<<": ";
typename std::list<T>::const_iterator iter = lists[i].begin();
while(iter != lists[i].end())
{
cout<<*iter<<" ";
++iter;
}
cout<<endl;
}
}
int nextPrime(const int n)
{
int ret,i;
ret = n;
while(1)
{
int flag = 1;
for(i=2;i<sqrt(ret);i++)
if(ret % i == 0)
{
flag = 0;
break;
}
if(flag == 1)
break;
else
{
ret = ret +1;
continue;
}
}
return ret;
}
class Employee
{
public:
Employee(){}
Employee(const string n,int s=0):name(n),salary(s){ }
const string & getName()const { return name; }
bool operator == (const Employee &rhs) const
{
return getName() == rhs.getName();
}
bool operator != (const Employee &rhs) const
{
return !(*this == rhs);
}
friend ostream& operator <<(ostream& out,const Employee& e)
{
out<<"("<<e.name<<","<<e.salary<<") ";
return out;
}
private:
string name;
int salary;
};
int main()
{
Employee e1("Tom",6000);
Employee e2("Anker",7000);
Employee e3("Jermey",8000);
Employee e4("Lucy",7500);
Employee e5("Tom1", 6000);
Employee e6("Anker1", 7000);
Employee e7("Jermey1", 8000);
Employee e8("Lucy1", 7500);
HashTable<Employee> emp_table(13);
emp_table.insert(e1);
emp_table.insert(e2);
emp_table.insert(e3);
emp_table.insert(e4);
emp_table.insert(e5);
emp_table.insert(e6);
emp_table.insert(e7);
emp_table.insert(e8);
cout<<"Hash table is: "<<endl;
emp_table.display();
if(emp_table.contains(e4) == 1)
cout<<"Lucy is exist in hash table"<<endl;
if(emp_table.remove(e1) == 1)
cout<<"Removing Tom form the hash table successfully"<<endl;
if(emp_table.contains(e1) == 1)
cout<<"Tom is exist in hash table"<<endl;
else
cout<<"Tom is not exist in hash table"<<endl;
emp_table.display();
exit(0);
}
/**
*备用注释:
*
*
*
*/
其运行效果如下所示:
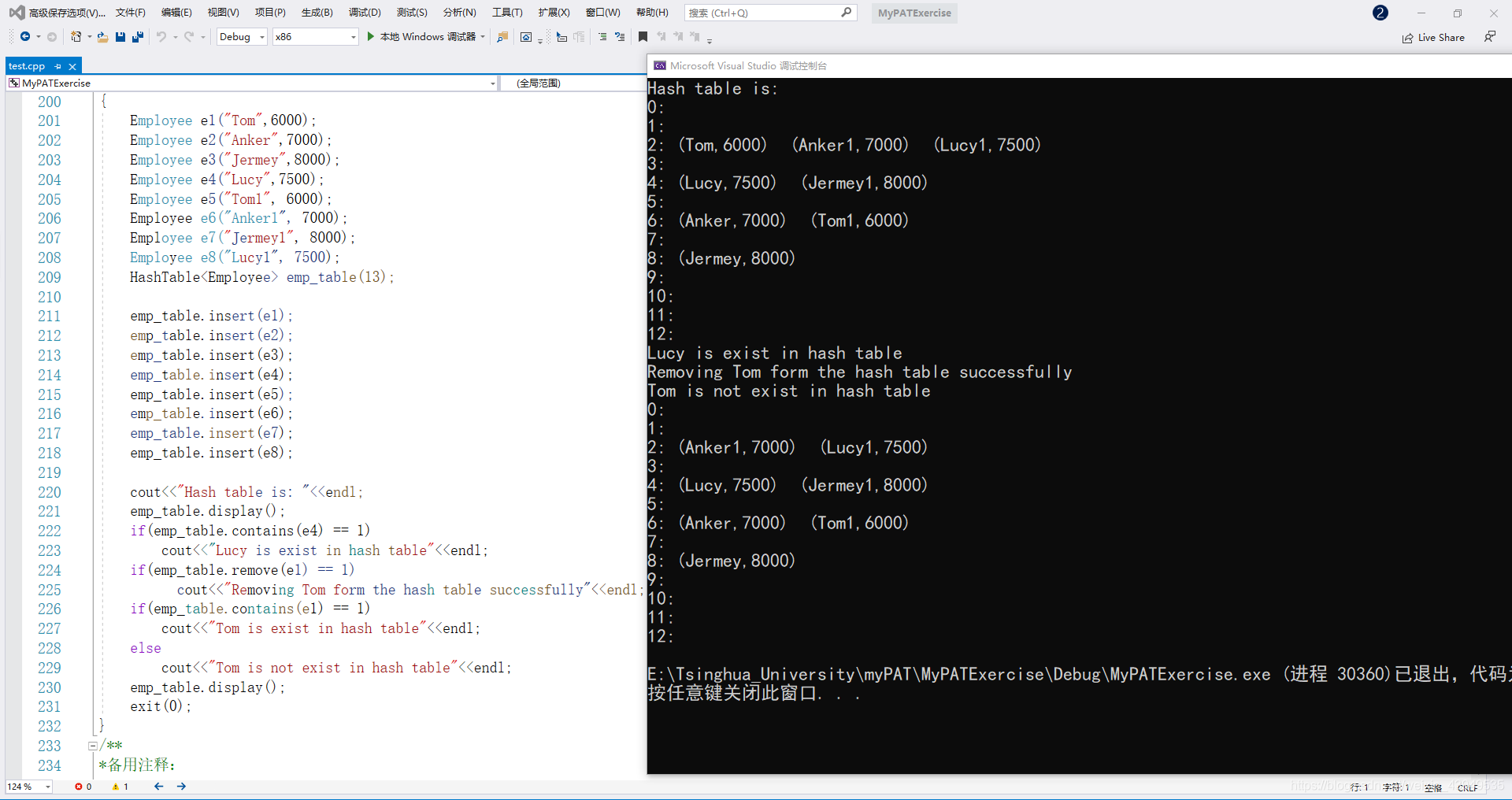
开放寻址法
开放寻址法概念:
1、所有元素都存放在线性的散列表里,每个槽位只存放一个元素:不需要链表,也没有元素存放在散列表之外。(也即:每个表项在不存储动态集合的某个元素外,其值即为nullptr)
2、当进行散列时,若是那个位置有值了,就在当前位置移动一定量的位置,然后再看有没有值;如果有值就再进行移动,直到有空位置 进行存放;但如果散列表满了,就无法存放了 下面可能涉及到扩容
3、开放导址法有很多种,多种的原因就在于:在当前位置移动一定量的位置。移动多少个位置,是每种方法的不同点
4、在Search某个元素的时候 要系统地检查所有的表项,直至找到所需的元素 或 查明该元素不存在
5、不同于链式地址法,既无链表也无元素存放在哈希表外。然而哈希表极有可能被填满,以至于无法插入任何新元素。在这种方法下 装载因子α=n/m绝对不会超过1
开放寻址法也是可以将 用作链接的链表存放在散列表未用的槽中,但使用开放寻址法的优势就在于不用指针,而是计算出要存取的槽序列。不用指针而节省的空间,使得可以用同样的空间来提供更多的槽,潜在地减少了冲突,极大地提高了检索速度。但开放寻址法,散列表可能会被填满,以至于不能插入任何新的元素。该方法直接的一个结果便是装载因子 α 不会超过 1。(装载因子 α = 数据个数 n / 槽数 m,既然是一个槽只能装一个元素,所以 n/m 不能超过1)
为了使用开放寻址法插入一个元素,需要连续地检查散列表,称为探查(probe),直到找到一个空槽来存放待插入的关键字为止。检查的顺序不一定是 0,1,…,m-1 (因为这种顺序的查找时间是O(n)),而是 依赖于待插入的关键字。为了确定要探查哪些槽,我们将散列函数加以扩充,使之包含探查号(从0开始)以作为其第二个输入参数。
对于每一个关键字 k,使用扩充的开放寻址法的 探查序列(probe sequence) 如下:
<h(k,0), h(k,1), h(k,2), ...h(k, m-1) >
// 上面就是<0,1,2,...,m-1>的一个存放排列
当散列表渐渐填满的时候,每个表位最终都可以被考虑为用来插入新关键字的槽。
下面是 这样的结构下,散列表T[]的字典操作展示。不过需要提前注意的是:
1、散列表T[]中的元素 是没有卫星数据的关键字,即:关键字k等同于 包含关键字k的元素
2、表中的每个槽 或包含一个关键字 或为nullptr(表示槽为空)
下面是过程 HASH_insert 以一个散列表T 和 关键字k为参数,返回结果:关键字k的存储位置 或者 因散列表满而返回出错标志。
HASH_insert(T,k)
{
for (int i = 0; i < m; ++i)
{
j = hash(k, i);
if (T[j] == nullptr)
{
T[j] = k;
return j;
}
}
printf("Hash table overflow\n");
return -1;
}
查找关键字k的算法的探查序列与将k插入时的算法一样。因此 当查找过程中碰到一个空槽时,查找算法即可停止。原因在于:若是k就在表内 它就应该在这个槽中,而不会在探查序列随后的位置上。(不过这里需要一个前提:假定了关键字不会从散列表里面删除)。过程HASH_search的输入 为一个散列表T 和 关键字k,返回结果:存在则返回其位置 槽号,不存在则给返回 -1
HASH_search(T,k)
{
for (int i = 0; i < m; ++i)
{
j = hash(k, i);
if (T[j] == nullptr)
{
return -1;
}
else if (T[j] == k)
{
return j;
}
}
return nullptr;
}
在开放寻址法的散列表中 删除操作元素 比较困难。当我们从槽 i 中 删除关键字时,不能仅将 nullptr 置于其中来标识它是空。
原因如下:
1、在插入关键字k的时候 若是此时槽 i 里面不为空(被占用),然后k就会被 插入到后面的位置上
2、可是一旦此时 将槽 i 置为空,那么就无法去检索到 后面的关键字 k 了
解决办法如下:在槽 i 中放置一个特定的值 例如DELETED替代nullptr来标记该槽。但是这样的话 就需要对上面的 HASH_insert 过程做出相应的修正:
HASH_insert(T,k)
{
for (int i = 0; i < m; ++i)
{
j = hash(k, i);
if (T[j] == nullptr || T[j] == DELETED)
{
T[j] = k;
return j;
}
}
printf("Hash table overflow\n");
return -1;
}
而对于HASH_search过程 无需做什么改动,因为在搜索的时候 会绕过DELETED标识符。但是 当我们在删除过程中使用 特殊的DELETED值时,查找时间就不再依赖于 装载因子 α了。(因为假设一个近满的表 被删的仅剩一个元素时 查找的时候还是会上面的遍历过程)。
为此,在必须要删除关键字的场景下,更常见的做法就是 使用链式地址法来解决冲突。
HASH_delete(T,j)
{
// 在T[]删除x j是其表的位置下标
T[j] = DELETED;
}
我们先为 计算开放寻址法中的探查序列 提供一个完美的假设(实际上难以实现):每个关键字的探查序列等可能地为 <0,1,2,...,m-1> 的 m! 种排列中的任一种,该假设被称为 均匀散列假设。均匀散列是将前面定义过的简单均匀散列的概念加以一般化 进而推广到散列函数的结果不只是一个数 而是一个完整的探查序列。可是这个均匀散列不太现实,在实际中 常常采用的还是其近似方法(如下的 双重散列)。
常用于计算开放寻址法中的探查序列的技术:线性探查、二次探查 和 双重探查。这几种技术都可以保证 对每个关键字k,<h(k,0), h(k,1), h(k,2), ...h(k, m-1) > 都是 <0,1,2,...,m-1> 的一个排列。但是这些技术并不能够满足均匀散列的假设,因为它们能够产生的不同探查序列数不超过 m2 个(均匀散列要求有 m! 个探查序列),在它们三者中:双重散列产生的探查序列数最多,似乎可以给出最好的结果。
线性探查
线性探查(Linear Probing):就是把 hash(k) 的值,再进行迭代加 i (i=0,1,2…m-1),来探查每个槽。该方法采用的散列函数如下:
// 辅助散列函数 hash'(k) 是一个普通的散列函数,U -> {0,1,2,...,m-1}
hash(k,i) = (hash'(k) + i) mod m, i = 0,1,...,m-1
/* 该方法的探查步骤如下:
1. 在给定一个关键字k,首先探查槽 T[hash'(k)] ,即由 辅助散列函数所给出的槽位
2. 然后再探查槽 T[hash'(k)+1] T[hash'(k)+2] 依此类推,直至 T[m-1]
3. 然后 又绕到槽 T[0] ,T[1] ... ...,直到最后探查到槽 T[hash'(k)-1]
*/
如上探测过程将在以下三种情况下停止:
- 若当前探测的槽为空,则表示查找失败(若是插入则将key写入其中)
- 若当前探测的槽中含有key,则查找成功,但对于插入意味着失败
- 若探测到
T[h'(k)-1]时仍未发现空单元也未找到key,则无论是查找还是插入均意味着失败(插入失败是因为此时表满)
如上 在线性探查中,初始探查位置决定了整个 探查序列 (所以 它只有 m 种不同的探查序列)。线性探查方法比较容易实现,但存在一个问题,称为一次群集(primary clustering)
1、随着连续被占用的槽不断增加,平均查找时间也随之不断增加(这个做法容易导致扎堆,即表中连续若干个位置都被使用,这将在一定程度上降低效率)
2、群集现象很容易出现 这是因为当 1 个空槽前有 i 个满的槽时,该空槽是下一个将被占用的概率是(i+1)/m
一次群集问题:连续被占用的槽的序列变的越来越长 性能也越来越差
采用例子进行说明线性探测过程,已知一组关键字为 十个数字:(26,36,41,38,44,15,68,12,6,51),用除留余数法构造散列函数(m=10),初始情况如下图所示:

下面就是如上一组关键字 经由线性探查下 哈希映射 插入到槽中的示意图:

- 我们这里着重关心一下 上面的第 9 10步(注意碰撞次数和继续查找次数)
hash(6,0)=6 hash(6,1)=7 hash(6,2)=8 hash(6,3)=9全部碰撞,直到掉头hash(6,4)=0OK 存放
hash(51,0)=1 hash(51,1)=2全部碰撞,直到hash(51,2)=3OK 存放
二次探查
二次探查法的探查序列采用如下形式的散列函数是:
h(k,i) =(h’(k) + c1 * i + c2 * i 2) % m ,0 ≤ i ≤ m-1
h’() 是辅助散列函数
c1 和 c2 是正数
初次的探测位置为T[h'(k)],后面的探测位置在该基础上加一个偏移量,该偏移量以二次的方式依赖于探查序号 i 。同理 和上面线性探查中一样,初始探查位置决定了整个序列,于是这也仅有 m 个不同的探查序列。
二次探查法的探查效果要比线性探查好很多,但是为了充分利用散列表, c1 、 c2 和 m 都应该受到限制。其优劣如下:
1、缺陷是不易探查到整个散列空间 会有浪费
2、优势在增加了常数c1 、 c2 来增加探查序列的分散性
此外 如果两个关键字的初始探查位置相同,那么它们的探查序列也是相同的,因为h(k1 , 0) = h(k2 , 0) 将标示着 h(k1 , i) = h(k1 , i)。这一性质将导致一种轻度的 clustering,称为二次群集(secondary clustering)。
这里有一个公理:若是 k 在 [0,m) 的范围内都无法找到位置,那么当 k>=m 的时候,也一定无法找到位置。
双重散列
双重散列(double hashing),是用于开放寻址法的最好的方法之一,因为它所产生的排列具有随机选择排列的许多特性。其采用如下形式的散列函数:
h(k,i) =(h1(k) + i * h2(k)) % m ,0 ≤ i ≤ m-1
h1(),h2()是辅助散列函数
其探查步骤:
- 第 1 次探查位置为 T[ h1(k) ]
- 接下来探查的位置是:( 前一个位置 + 偏移量 h2(k) ) mod m
- 循环第 2 步
这样做的优势在于:不像线性探查或者二次探查,这里的探查序列以两种不同的方式来依赖于关键字 k,毕竟 初始探查位置、偏移量或者二者都会发生改变。因为每一对可能的(h1(k),h2(k))都会产生一个不同的探查序列,因此对于 m 的每一种可能取值,双重散列的性能看起来就比较接近于最上面所说的 均匀散列 的性能。
为了可以去查找整个散列表,值 h2(k)就必须要和 表的大小 m 互素。下面有两种实现办法:
1、取 m 为2的幂,h2() 是一个产生奇数的散列函数
2、取 m 为素数, h2() 是一个返回 较 m 小的正整数的散列函数
为什么要是互素呢?因为若 a 与 b 互质,那么 (a * i) mod b 在 i=0,1,2…,b-1时,正好可以形成 {0, 1, 2 … b-1}的排列组合(就是置换)示例如下:
// a=5,b=8
i=0 (5×0=0) mod 8=0
i=1 (5×1=5) mod 8=5
i=2 (5×2=10) mod 8=2
i=3 (5×3=15) mod 8=7
i=4 (5×4=20) mod 8=4
i=5 (5×5=25) mod 8=1
i=6 (5×6=30) mod 8=6
i=7 (5×7=35) mod 8=3
下面举一个例子,采用上面第二种方法:
1、h1(k) = k % m
2、h2(k) = 1 + k % p
3、p 略小于 m,例如 p = m-1
①、k=123456
②、m=701
③、p=700
h1(k) = 80,h2(k) = 257
于是如上:第一个探查位置是 80,然后检查每第257个槽 (模m),直到找到该关键字,或者遍历了所有的槽
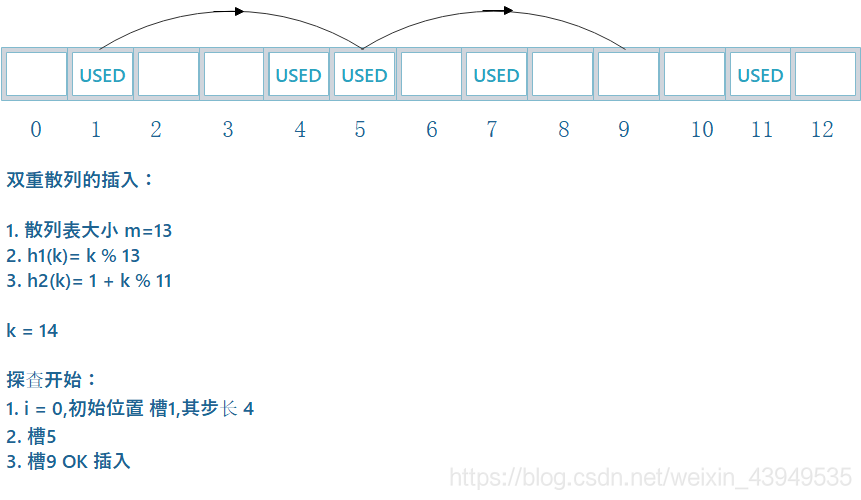
当 m 为素数或者为 2 的幂时,双重散列中用到了 O(m2)种探查序列,而上面的线性探查 二次探查用到了 O(m)种探查序列,所以前者相较于后两者是一种改进。
尽管 除去素数和2的幂以外的 m值在理论上也可以应用在 双重散列之上,但是在实际中 想要高效地产生h2(k) 确保与 m 互素将是非常困难的。
开放寻址法的性能分析:
同链式地址法一样,开放寻址法的分析也是以 散列表的 装载因子 α=n/m 来展开的。但是在开放寻址法中,1个槽至多一个元素,即:n <= m,α=n/m <= 1
假设采用的是均匀散列,在这种理想的方法下 用于查找或者插入操作的 每一个关键字k对应的探查序列 <h(k,0), h(k,1), h(k,2), ...,h(k, m-1) > 等可能地为 <0,1,2,...,m-1> 的任意一种排列。当然 每一个给定的关键字k有其相应的唯一固定的探查序列。这里想说的是:在考虑到关键字空间上的概率分布以及散列函数施于这些关键字上的操作,每一种探查序列都是等可能性的。
下面是书中的定理:
1、在均匀散列的假设下,使用开放寻址法(装载因子
α=n/m< 1) 进行散列时探查的期望次数:对于一次不成功的查找,其期望的探查次数至多是 1/(1-α)
2、同理 在均匀散列的假设下,使用开放寻址法(装载因子α=n/m< 1),平均情况下 向该散列表中插入一个元素至多需要 做 1/(1-α) 探查
3、在均匀散列的假设下,使用开放寻址法(装载因子α=n/m< 1) 进行散列时探查的期望次数:对于一次成功的查找 其探查期望数至多为-ln(1-α)/α证明如下:
完全散列法
使用散列技术通常是个好的选择,不仅是因为它有优异的平均性能,而且当关键字集合是静态的时,散列技术也能提供出色的最坏情况的性能。所谓静态,就是指一旦各关键字存入表中,关键字集合就不再变化了。一些应用存在着天然的静态关键字集合,如程序设计语言中的保留字集合,或者CD-ROM上的文件名集合。完全散列 perfect-hashing,采用两级散列的方法来设计完全散列方案。(在该方法下进行查找时,可在最坏情况下 O(1)时间下完成 因为二级散列表没有冲突,因而Search操作最坏情况时间复杂度为 常数)
在形式上 完全散列和链式地址法散列有点像,只不过每个结点又一是个散列,而非链表。形式如下图所示:
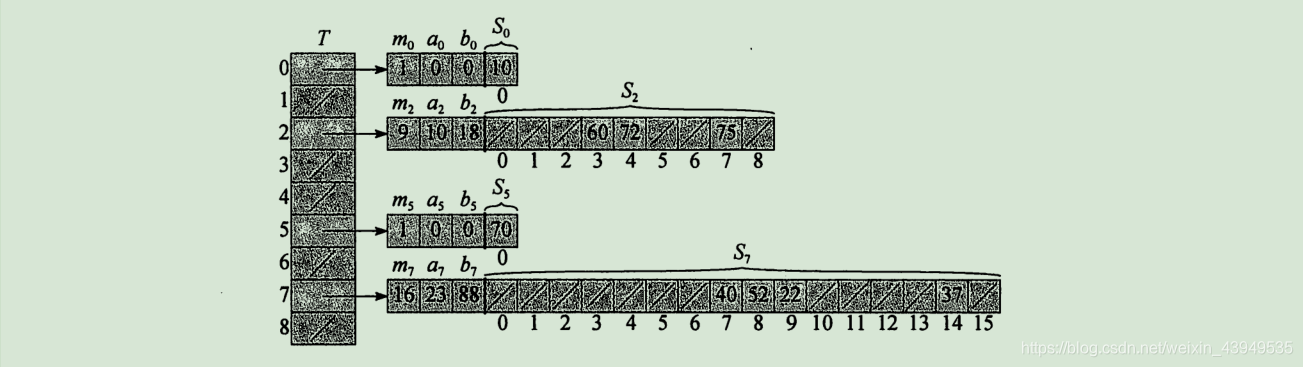
如上图所示:第一级与带链接的散列表基本上是一样的:利用从某一全域散列函数簇中仔细选出一个散列函数h,将n个关键字散列到m个槽中。然而,我们采用一个较小的二次散列表(secondary hash table) Sj,及相关的散列函数hj,而不是将散列到槽j的所有关键字建立一个链表。利用精心选择的散列函数hj,可以确保在二级散列上不出现冲突。但是 为了确保第二级上不冲突,需要让散列表 Sj 的大小 mj,为散列到槽j中的关键字数 nj 的平方。
这段话不是很好理解,先行看过一个例子(上图):
如上,这个完全散列表是由两个散列表组成,竖向的是一级散列表,横向的是二级散列表。把一个 k 加入到散列表中过程如下:
1、首先用 h(k) 函数算出 关键字k 在一级散列表中的槽位 h(k) = ((ak+b) % p) % m
2、再用 h(k) 公式和二级散列表中的参数,算出 k 在二级散列中的位置。该二级散列Sj 里面存放了 所有被散列到槽 j 的关键字 hj(k) = ((ajk+bj) % p) % mj
例如,k=75,散列函数为
h(k)=(((a * k + b) mod p) mod m),且 a=3,b=42,p=101,m=9
1、一级散列表的位置是:(((3 * 75 + 42) mod 101) mod 9 = 2,所以首先把 k 放到 2 号槽位里面
2、接下来,二级散列中有 a2、b2、m2 这三个参数,用这三个参数替换一级散列中的相应的 a、b、m 参数,则 h(k) = (((10 * 75 + 18) mod 101) mod 9 = 7,所以把 k 放到二级散列的 7 号槽位上
如上图所示:二级散列表 Sj 的大小 mj,是散列到槽j中的关键字数 nj 的平方。尽管 mj 对于 nj的这种二次依赖 看起来 可能使得总体的存储需求会很大,但是在适当选择 第一级散列函数之后,是可以将预期使用的总体存储空间限制在 O(n)的。
接下来有两个问题需要研究以下的:
这里采用的哈希函数都是来自于 全域散列函数类的;上面的 p 值是一个比任何关键字都要大的素数
1、如何做到第二级散列不发生 冲突
2、如何保证 总体存储空间期望为 O(n):包括主散列表 + 所有二级散列表的空间
关于上面第一点,书中给出的证明 我感觉是在糊弄小孩儿 😀(其实是有道理的,只是感觉有种 只可意会不可言传 的感觉):

下面给出个人的理解(有问题 小伙伴们请在评论区留言):
请大家时刻注意 完全散列法的一些使用场景相关:关键字集合是静态的时候
- 完全散列只能用于固定的关键字 注意静态二字,而不是任何可以用散列的情况。只有在这种情况下才可能完全避免冲突
- 如果待散列的关键字不是固定的,可能无论怎么尝试也找不到不碰撞的散列函数。数学上只证明了对固定关键字,一定能找到无碰撞函数
- 完全散列的关键就是第二次散列要找到一个不会冲突的散列函数
- 如果第二次散列无法找到不冲突的函数(有固定方法,绝对不是瞎凑),就需要修改第一次散列的函数。数学上证明了: 当桶的数目超过关键字数目2倍时,经过足够多次的尝试,总是能够找到不冲突的散列方法
- 找到不冲突的散列函数的尝试次数平均为O(1),但最坏情况下为O(n)。 完全散列其实是把查找时的复杂度转移到了算法设计的过程中 换句话说:性能的强悍在于:设计的好。举个例子:当桶的数目是关键字数目3倍时, 平均尝试1.7次即可找到无碰撞的散列函数。但是运气不好的话,最大次数是无穷多次,但是这种概率非常非常低
- 如果把完全散列应用到一般散列的情况, 效果也不错。但是第二次散列可能产生冲突,查找的最坏时间就变成O(n)
OK,下面来看 空间损耗的证明:
由于 第 j 个二级散列表的空间为 mj = nj 2,这种随所存储关键字个数以平方级的增长方式 确实会存在 总体存储空间使用 很大的风险
我们先设想一下这个场景:我有10个关键字,可是经过一级哈希之后 被映射到 同一个一级槽中,然后导致二级哈希表的空间达到了100左右。那么出现这种情况的根源在哪里?就是一级哈希函数的问题,你不应该映射到一个槽中。理想情况下:一级哈希直接映射到10个不同的槽(每个槽一个key),那么10个二级哈希表的长度也才总共是10 * 1* 1
然后再来看一下书中说的一句话:

OK,下面就来看一下其证明过程:
对于一级哈希表的大小:m=n,用于存储 一级散列表 + 大小为 mj 的二级散列表 + 用于存储二级哈希函数 hj 的参数 aj 和 bj 。其存储空间总量在 O(n)
下面主要关注于 所有二级哈希表的空间总值:

由上图可得:只需要从全域散列函数类中 随机选择几个哈希函数,多尝试几次 即可得到一个所需存储量较为合理的哈希函数。
非常遗憾,我们通常没有办法检查此条件是否成立。因为一来很少知道 关键字散列 所满足的概率分布,二来关键字间可能并不是完全独立的 ↩︎








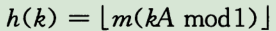















 324
324











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










