牛客 OI 赛前集训营-提高组（第一场）C - 与巨——二进制、结论

进不去的题面

题目描述

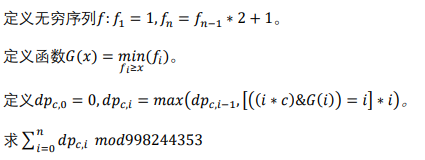
题解

首先可以发现，$G(i)$ 的二进制最高位以前全是1，而且最高位和 $i$ 相同，所以 $[(i\ast c)\&G(i)=i]$ 相当于 $i$ 乘以 $c$ 过后，原来的数位上不变。

考虑什么情况下原来的数位不会变。如果 $c$ 是偶数，那么 $i\ast c$ 和 $i$ 的最低位必定不相同，所以答案为0。如果 $c$ 是1，那么显然每个数都符合要求。

如果 $c$ 是不为1的奇数？考虑 $c$ 的二进制表示的最后两个1：一个是1，一个是 $g=\mathrm{l}\mathrm{o}\mathrm{w}\mathrm{b}\mathrm{i}\mathrm{t}(\mathrm{c}-1)$。

...001000001  c
       10111  i
     1011010  i
    10101100  i
	...

若 $i<g$ 那么显然可以；
若 $i$ 的最高位和 $g$ 相同，此时 $i$ 的最后一位必须为0，否则在最高位以前必定和原数不同；
若 $i$ 的最高位比 $g$ 大一位，此时 $i$ 的最后两位必须为0，否则在最高位以前必定和原数不同；
以此类推。

于是可以得到结论：假设 $g=2^w$，那么符合条件的 $i$ 必须满足二进制只有最高的 $w$ 位以内存在1，其它位上必须全为0。由于 $d{p}_{c,i}$ 是求前缀最大值，所以 $d{p}_{c,i}$ 就等于 $i$ 保留最高的 $w$ 位的结果。

知道了结论过后，我们只需要设计一下怎么在 $O(|n|)$ 复杂度以内统计答案即可。

$c$ 为偶数直接输出0，$c$ 为1则直接用公式计算 $0\sim n$ 的等差数列求和即可。

对于其它情况，我们可以枚举数的最高位 $i$，如果位数 $i<|n|$，那么前 $w$ 位的每一种值都要被计算 $2^{i-w}$ 次，所以只需要用等差数列求和计算一下前 $w$ 位的值的和。

如果位数 $i=|n|$，那么在前 $w$ 位没取到最大时，仍然每一种都会被计算 $2^{|n|-w}$ 次，而前 $w$ 位的最大值会被计算 $(n\mathrm{m}\mathrm{o}\mathrm{d}{2}^{|n|-w})+1$（$n$ 的后 $|n|-w$ 位的值+1）次，再次用等差数列求和计算即可。

代码

#include<cstdio>//JZM yyds!!
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<ctime>
#include<vector>
#include<queue>
#include<stack>
#include<map>
#include<set>
#define ll long long
#define uns unsigned
#define MOD 998244353ll
#define MAXN 10000005
#define INF 1e18
#define lowbit(x) ((x)&(-(x)))
#define IF it->first
#define IS it->second
using namespace std;
inline ll read(){
	ll x=0;bool f=1;char s=getchar();
	while((s<'0'||s>'9')&&s>0)f^=(s=='-'),s=getchar();
	while(s>='0'&&s<='9')x=(x<<1)+(x<<3)+(s^48),s=getchar();
	return f?x:-x;
}
inline ll ksm(ll a,ll b,ll mo){
	ll res=1;
	for(;b;b>>=1,a=a*a%mo)if(b&1)res=res*a%mo;
	return res;
}
const ll iv2=((MOD+1)>>1);
char s[MAXN];
int n;
ll c,mi[MAXN];
inline int AD(int a,int b){
	a+=b;return a>=MOD?a-MOD:a;
}
inline void init(int n){
	mi[0]=1;
	for(int i=1;i<=n;i++)mi[i]=AD(mi[i-1],mi[i-1]);
}
signed main()
{
	init(10000000);
	for(int T=read();T--;){
		scanf("%s",s+1),n=strlen(s+1);
		c=read();
		if(~c&1){
			printf("0\n");
			continue;
		}
		if(c==1){
			ll f=0;
			for(int i=1;i<=n;i++)f=((f<<1)+(s[i]^48))%MOD;
			printf("%lld\n",f*(f+1)%MOD*iv2%MOD);
			continue;
		}
		ll ans=0;
		ll g=lowbit(c^1);
		int w=0;
		while((1ll<<w)<g)w++;
		for(int i=n,j=0;i>1;i--,j++){
			int e=min(w-1,j);
			ll p=1ll<<e,sum=(p*3-1)%MOD*(p%MOD)%MOD*iv2%MOD;
			ans=AD(ans,sum*mi[j-e]%MOD*mi[j-e]%MOD);
		}
		int e=min(w-1,n-1);
		ll f=0,sl=0;
		for(int i=2;i<=e+1;i++)f=((f<<1)+(s[i]^48))%MOD;
		ll sum=((1ll<<(e+1))%MOD+f+MOD-1)%MOD*f%MOD*iv2%MOD;
		ans=AD(ans,sum*ksm(2,(n-e-1)<<1,MOD)%MOD);
		f=AD(f,(1ll<<e)%MOD)*ksm(2,n-e-1,MOD)%MOD;
		for(int i=e+2;i<=n;i++)sl=((sl<<1)+(s[i]^48))%MOD;
		ans=AD(ans,f*(sl+1)%MOD);
		printf("%lld\n",ans);
	}
	return 0;
}