浅谈公平博弈

抄的PPT

公平博弈

虽然公平不等于平等，但是公平博弈，也叫平等博弈。

前置知识：超现实数、非平等博弈

指在不平等博弈的基础上，双方的操作等同，形式化地，若博弈 G = { L ∣ R } , L = R G=\{L|R\},L=R G={L∣R},L=R ，则它是个公平博弈，我们把它简写为 G = { L } G=\{L\} G={L}。

公平博弈要么先手必胜要么后手必胜，所以 $G=0$ 或 $G||0$ ，且有 $G+G=0$ 。所以对于公平博弈来说，加法和减法是等价的，$G+H=G-H$。

Nim 游戏

这里我们先讨论只有一个石子堆的情况。

若一堆石子有 $n$ 个，我们可以称它为一个 Nim 堆，用 $\ast n$ 表示，根据定义：
∗ n = { 0 , ∗ , ∗ 2 , ∗ 3 , . . . , ∗ ( n − 1 ) } *n=\{0,*,*2,*3,...,*(n-1)\} ∗n={0,∗,∗2,∗3,...,∗(n−1)}

很明显当 $n>0$ 是先手必胜，直接取完，否则后手必胜。

任何公平博弈都可以最终等价为一个 Nim 堆。感性理解，是否有 $\ast$ 号决定它的结果，后面的数字刻画了它的过程。同时说明所有的后手必胜的博弈没有本质区别。

一个 Nim 堆也是一个 Nimber 。

SG 定理

若 $G$ 是有限状态的公平博弈， G = { ∗ a , ∗ b , ∗ c , . . . } = ∗ n G=\{*a,*b,*c,...\}=*n G={∗a,∗b,∗c,...}=∗n ，那么 n = m e x { a , b , c , . . . } n=\mathrm m\mathrm e\mathrm x\{a,b,c,...\} n=mex{a,b,c,...} ，$\mathrm{m}\mathrm{e}\mathrm{x}$ 指最小不在集合中的自然数。

这个结论相信大家就算不熟悉，也听说过很多次了。证明很简单，运用博弈加法的定义分类讨论证 $G+(\ast n)=0$ 就行了。

Nim 和

即多个 Nim 堆放一起博弈，也是公平博弈的加法，Nimber 和。

若 $\ast n=\ast a+\ast b$，那么 $n=a\oplus b$ 。

这就是 Nim 游戏的一般结论，相信大家更加熟悉了。

证明有很多，可以从博弈加法和 SG 定理角度证明，也可以用 Nim 游戏的经典证明

常见公平博弈模型

Bash 博弈

n 个石子，每次至少取一个，最多取 m 个，先取光的胜。

用 SG 定理想一下，不难发现该博弈等于 $\ast (n\%(m+1))$ 。

Nim 博弈

Impartial Combinatorial Games（ICG） 的祖师爷。

有 $n$ 堆石子，A 和 B 每次轮流选一堆石子取走正整数个，取走最后一个石子的人获胜。

每一堆石子就是等值的 Nim 堆，整个博弈等于所有的 Nim 堆相加，数值上为异或和。

Nim-K 博弈

n 堆石子，每次可以选最少 1 堆、最多 k 堆石子，在这些堆石子里面任意拿，每堆最少拿一颗，先取光的胜。

把这 n 堆石子的数量转成二进制，然后在每一位上加起来，如果每一位都是 k+1 的倍数，那么后手胜，否则先手胜。

• 证明：和 Nim 和的证明类似，对于某个局面，若存在某些二进制位上的 1 的个数 mod (k + 1) 不为 0，则一定存在一个合法的移动，使得每一个二进制位上的 1 的个数 mod(k + 1) 等于 0 。

转化成 $\ast n$ 的形式，可以，但没有规律。

Wythoff 博弈

有 2 堆石子，每人每次可以拿走任意一堆中任意数量的石子或在两堆石子中拿走相同数量的石子，不能拿的人输。

用 $(a,b)$ 表示一个状态，可以发现后手必胜的 $a$ 和 $b$ 为自然数集的一个分割，那么由 betty 定理可以得到一个很美观的结论：

后手必胜的状态集合为 P = { ( a i , b i ) ∣ a i = ⌊ 1 + 5 2 i ⌋ , b i = a i + i , i ∈ N } P=\{(a_i,b_i)|a_i=\left\lfloor\frac{1+\sqrt5}{2}i\right\rfloor,b_i=a_i+i,i\in N\} P={(ai​,bi​)∣ai​=⌊21+5 ​​i⌋,bi​=ai​+i,i∈N} ，记住那个黄金分割率。

扩展：有 2 堆石子，每人每次可以拿走任意一堆中任意数量的石子或在两堆石子中数量差 $\le k$ 的石子，不能拿的人输。这个博弈的后手必胜状态也有规律，满足 a i = m e x { a j , b j ∣ j < i } , b i = a i + ( k + 1 ) i a_i=mex\{a_j,b_j|j<i\},b_i=a_i+(k+1)i ai​=mex{aj​,bj​∣j<i},bi​=ai​+(k+1)i。然后套用 betty 定理。

Fibonacci 博弈

1堆石子有 n 个，两人轮流取，先取者第 1 次可以取任意多个，但不能全部取完，以后每次取的石子数不能超过上次取子数的2倍，取完最后一个石子胜。

找规律可知若 n 是斐波那契数，那么先手必败，否则必胜。

证明超纲，不拉了。

阶梯博弈

$1\times \infty$ 的棋盘上有 $n$ 个棋子，每次可以选一个棋子往左挪若干步，不能越过棋子以及左边界，不能走者败。

结论：从右往左数，将相邻的两个旗子依次配对，第一个棋子可与左端点配对。把每一对中间的空位数等价为 Nim 堆，然后求 Nim 和。

Green Hackenbush

属于非平等博弈中 $\mathtt{H}\mathtt{a}\mathtt{c}\mathtt{k}\mathtt{e}\mathtt{n}\mathtt{b}\mathtt{u}\mathtt{s}\mathtt{h}$ 问题中全是绿边的子问题。全是绿边变成了公平博弈。

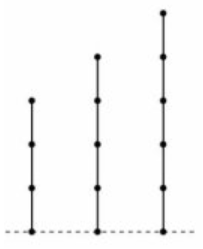
链的情况

一条长度为 $n$ 的链相当于一个 $Nim$ 堆 $\ast n$ 。

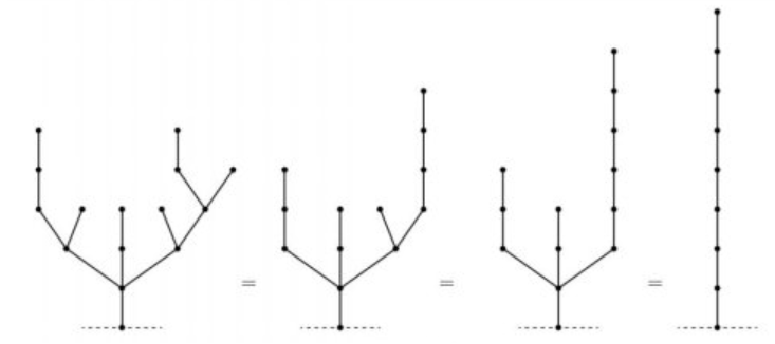
树的情况

如果一棵子树为 $\ast x$，我们就可以把它变成一条等价的链，然后转移到父亲那里会多一条边，变成 $\ast (x+1)$，然后和别的子树博弈加起来（数值异或），作为父亲的 Nimber。

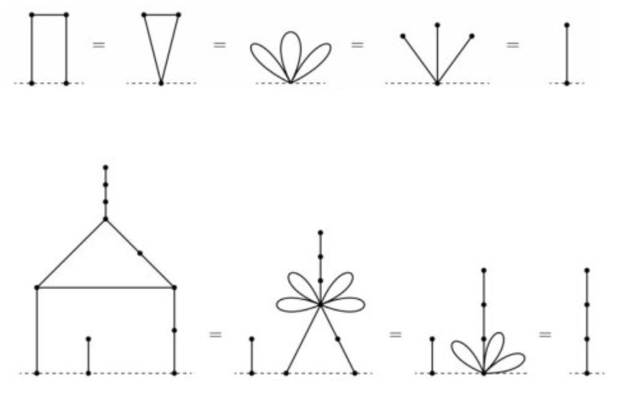
存在环

一个环内的两个相邻节点，可以合并为一个点，然后相连的边变成自环。

一个自环相当于一个叶子。

再根据树的规则转化。