详细讲解最小生成树

要知道什么是最小生成树（最小代价生成树），就要知道生成树的概念。
生成树：包含图中全部顶点，但只有足以构成一棵树的n-1条边。
而最小生成树就是在生成树的条件中，再加上一个条件：使得权值之和最小。

我们可以将其抽象化为这样一个例子：
假设要在n个城市之间建立通信联络网，则连通n个城市只需要n-1条线路。这时，自然会考虑这样一个问题：如何在最节省经费的前提下建立这个通信网络。

那么，怎么构造最小生成树呢？
下面介绍两个算法：
（1）普里姆算法(Prim)
（2）克鲁斯卡尔算法(Kruskal)

（1）普里姆算法(Prim)
普里姆算法的构造过程：
假设N=（V,E）是连通网，TE是N上最小生成树中边的集合。
a.U={u0}（u0∈V），TE={}
b.在所有u∈U，v∈V-U的边(u,v)∈E中找一条权值最小的边(u0,v0)并入集合TE，同时v0并入U
c.重复b，直至U=V

下面是一个例子：

最后得到的生成树为：

注意：每次选取最小边时，可能存在多条同样权值的边可选，此时任选其一即可。

（2）克鲁斯卡尔算法(Kruskal)
关键的两点：
（1）这条边连接两个不同的连通分量
（2）这条边的权值最小

例子：
依然使用上面的那个例子来讲：


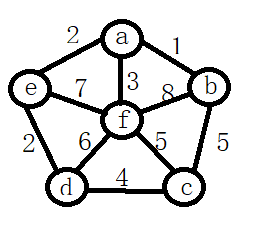
Prim算法适合构造一个稠密图G的最小生成树，Kruskal算法适合构造一个稀疏图G的最小生成树。