CTDA读书笔记1：Morse引理及Morse函数

CTDA读书笔记1：Morse引理及Morse函数

背景

定义在光滑流形上的光滑函数$f:M\to \mathbb{R}$的临界点为流形上梯度场等于0向量的点。临界点由其hessian矩阵的奇异性分为退化临界点和非退化临界点。实际中重点关注的是非退化临界点，例如定义在${\mathbb{R}}^2$上的实值函数$f:{\mathbb{R}}^2\to \mathbb{R}$的非退化临界点包括极大极小值点和鞍点。

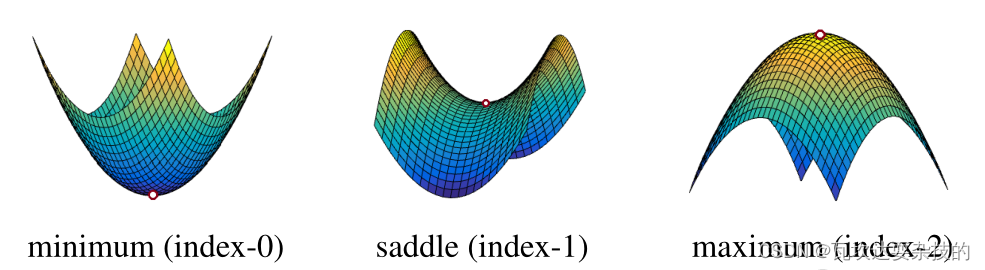
Morse引理描述了非退化临界点的邻域特征。（通俗理解就是按邻域特征将函数的非退化临界点分类了）

Morse引理

给定一个定义在光滑m-maniflod $M$上的光滑函数$f:M\to \mathbb{R}$，设$p$为$f$的非退化临界点。在$p$的邻域$U(p)$中存在一个以$p$为原点的$m$维坐标系，使得对$U(p)$中的任意点$x=(x_1,x_2,\dots ,x_m)$有
$$f(x)=f(p)-x_1^2-\dots x_s^2+x_{s+1}^2\dots x_m^2,\text{ for some }s\in [0,m]$$
上式中负号的个数称为非退化临界点$p$的index。

特别的，index-0非退化极值点即为极小值点，index-m非退化极值点即为极大值点。剩余的index-$(m-1)$个非退化极值点为不同类型的鞍点。

index	type
0	minimum
[1, m-1]	saddle
m	maximum

Morse函数

Morse函数是一类相当nice的函数，其临界点均为非退化的。
定义（ Morse函数）：定义在光滑m-maniflod $M$上的光滑函数$f:M\to \mathbb{R}$为Morse函数当且仅当：
（i）$f$的所有临界点都是非退化的；
（ii）$f$的所有临界点有不同的函数值。

参考文献

[1] Dey T K, Wang Y. Computational topology for data analysis[M]. Cambridge University Press, 2022.