李宏毅机器学习第1周_Introduction of Deep Learning

摘要

在本周共学习了三部分内容。了解了本课程框架、机器学习基本概念。通过预测油管浏览量的例子学习了线性模型、sigmoid函数、ReLU和全连接前馈网络。了解了一种计算微分的有效方式——反向传播。

ABSTRACT

In this week’s study, I learned three parts. Learn about this course framework, basic machine learning concepts. Linear models, sigmoid functions, ReLU and fully connected feed-forward networks were learned by predicting tubing views. Learn about an efficient way to calculate differentiation – backpropagation.

课程框架

教机器的种种方法

1. 监督学习 Supervised Learning Lecture 1-5
2. 自我监督学习 Self-Supervised Learning Lecture 7
   • Pre-trained Model vs Downstream Tasks
3. 生成对抗网络 Generative Adversarial Network Lecture 6
   • Unsupervised Abstractive Summarization
   • Unsupervised Translation
   • Unsupervised ASR（ASR，语音识别）
4. 强化学习 Reinforcement Learning Lecture 12

进阶课题

1. 异常检测 Anomaly Detection Lecture 8
2. 可释性人工智能 Explainable AI Lecture 9
3. 模型攻击 Model Attack Lecture 10
4. 域适配 Domain Adaptation Lecture 11
5. 网络压缩 Network Compression Lecture 13
6. 终身学习 Life-long Learning Lecture 14

Meta Learning = Learn to Learn

• Meta learning Lecture 15

机器学习基本概念

Machine Learning ≈ Looking for Function

机器学习，即找到用于完成任务的程式

任务可以是Speech Recognition、Image Recognition或Playing Go

Different types of Functions

不同种类的程式，程式的input、output具有多样性

input可以是vector、matrix或Sequence等

output可以是scalar、class、text或image

Regression: output为值(scalar)的function

Classification: 给出多个选择(classes)，function会给出其中正确的一个

eg: Playing Go任务是Classification，给出的选择是棋盘上可以落子的各点位

Structure Learning: 通过该类学习可以赋予网络结构性创造的功能

预测油管某天的浏览量

Linear model

1. Function with Unknown Parameters

   • 写一个带有未知参数的程式
   • y = b + wx₁ Model线性模型
     • x₁与y是特征值feature
     • b与w为未知参数
     • x₁：某天前一日的浏览量
     • y：预测的某天的浏览量
     • b：偏差 bias
     • w：权重 weight
     • 

2. Define Loss from Training Data

   • Loss是function中的一个参数，表明这组参数的优劣

   • Loss越大，表明这组参数选择越不好；越小表明选择越好

   • 标签值y’为实际值，y为预测值，根据这两个数据可以计算出LOSS

   • 

   • 

   • 可以采用MAE（平均绝对误差）和MSE（平均平方误差）两种方式计算LOSS

   • 

   • 依据LOSS值可以绘制出Error Surface（误差平面）

   • 下图中，越接近红色，误差越大；越接近蓝色，误差越小

   • 

3. Optimization

   • 求w^*, b^*，使得其对应的L最小
   • Gradient Descent梯度下降
     • 单个特征值的情况

       • 随机选取初始值w⁰

       • 计算在w=w⁰，w对于L的微分

       • 计算w¹，

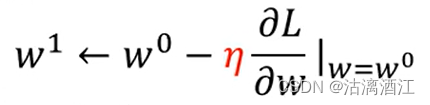
         • η: learning rate 学习率

       • 迭代的更新w

       • 

     • 注：可能求得极小值local minima，但不一定是最小值global minima
     • 多个特征值的情况
       • 
   • 经过观察，浏览量呈现7天为一周期。可以用下图程式作为计算程式，考虑7天的数据并分别赋予w_n权重
     

   More flexible model

线性模型过于简单，有着诸多限制，会产生模型限制（model bias），因此需要一个更为复杂的模型

对于红色曲线，可以表示成常数与多个蓝色程式的和，蓝色程式仅以在一定阈值（threshold）斜率不为零

对于非分段线性程式的连续曲线，可以通过分段线性曲线的近似连续曲线，为了获取更近似的分段线性程式，我们需要充足的蓝色程式

Sigmoid function

蓝色程式称作hard sigmoid，可以使用sigmoid function表达，即y = c/[ 1 + e^-(b+w*x1)] = c*sigmoid(b + wx₁)。调整参数c、b以及w以获得更合适的sigmoid function

w控制坡度slope，不同的b可以将曲线左右移动shift，不同的c可以改变高度height

当引入sigmoid之后，单feature的①转化为②，多feature的③转化为④

对于三个feature、三个sigmoid function的情况，y = b + c^Tσ( b + Wx )

注：3个feature也可以对应更多的sigmoid，这样可以得到更近似的piecewise linear，sigmoid数量可以试作hyperparameter

sigmoid function的ML Framework

1. Function with Unknown Parameters

   • 

2. Define Loss from Training Data

   • 本步骤内容与linear function的情况类似，赋值各参数θ、代入feature、计算预测值与label的误差e，最后L(θ) = 1/N(∑_ne_n)
   • 

3. Optimization

   • 随机取初始值->计算gradient直至g_n为零向量或者满意为止

   • 

   • 注：实际上，可能总样本N比较大，需要将N随即划分为多个batch，在分别计算各batch的L。完成一个batch之后进行一次update，当遍历所有batch之后称完成一次epoch

     • 对于1000 examples, batch size = 100，1 epoch有10 updates

ReLu

ReLU，rectified linear unit，修正线性单元，定义为f(x) = c max(0, b + w x₁)。当b+wx₁>0，该函数被激活f(x) = cx；当b+wx₁<0，f(x)=0。若要使用ReLU函数表示sigmoid，则需要两个ReLU表示一个sigmoid。
ReLU与sigmoid都是深度学习中重要的激活函数

Neural networks

可以将一组程式基于feature的计算结果作为另一组的feature，将程式按层嵌套，一组function称作1layer
深度学习，即多个hidden layer组合的神经网络（Deep = Many hidden layers）

优化方式：

• 扩宽网络，为一层添加更多的ReLU
• 加深网络，使用更多layer的神经网络
• 当网络过深，可能出现Overfitting，在已知数据（训练集）上表现得效果更好，在未知数据（验证机）上表现却更差
  • 

Deep Learning

Fully Connect Feedforward Network

全连接前馈网络，其是一组带有参数的函数组，输入为向量，输出为向量。若仅给出network structure，则称定义了一组function set。

前一层中每个neuron会传递到后一层的neuron中，故称全连接，又传递从前向后，故称正向传递。

neural network是嵌套的matrix operation，可用并行计算技术加速

• input layer是一组feature。
• 而hidden layers提取特征，相当于feature extractor
• 最后output layer作为multi-class Classifier（分类器），可以使用softmax function
  • 该层各维数据对应各类的置信度
    
    对于分类的预测值，可以使用预测值与目标值的交叉积作为Loss，同样可以使用梯度下降的方式进行优化

Backpropagation

backpropagation是一种计算微分的有效方式

loss等式两侧计算对某个w计算偏微分

计算z对w的偏微分，称作向前传递；即与权值相连的输入
计算C对w的偏微分，称作向后传递；

backward pass将后几层的误差反馈到本层的LOSS