数论——板子

玛咖二锅头

已于 2022-05-07 00:32:38 修改

阅读量446

点赞数

分类专栏： ACM板子文章标签：几何学算法

于 2021-01-27 11:33:33 首次发布

本文链接：https://blog.csdn.net/weixin_44224825/article/details/106623158

版权

ACM板子专栏收录该内容

9 篇文章 2 订阅

订阅专栏

数论

欧几里得算法证明 O（ logn ）

gcd

求A和B的最大公约数
假设X为最大公约数
间接条件：X | A X | B

假设A >= B
建立方程式A + KB = C = A % B
∵ X | A X | KB
∴ X | A + KB
∴ X | C
∴ GCD（A,B）== GCD（B, A%B）
然后我们就可以不断的往下辗转相除

求GCD（B,C）
B和C最大公约数也是X
何时是个头
GCD（KX , X ）其实这里能被整除，就已经知道求到GCD了
再往下
GCD （X , 0）

扩展欧几里得 O（ logn ）

exgcd

前提条件：d==gcd(a,b)
问题：ax+by=d,求x和y的通解

那么我们先建立一个方程组
A：ax1 + by1= d ==gcd(a,b)
B：bx2 + a%by2= d ==gcd(b,a%b)

B方程式展开：bx2 + ( a - a / b * b ) * y2=d
括号打开再合并：ay2 + b * ( x2 - a / b * y2 ) = d
所以：
x1=y2
y1=x2 - a / b * y2
不断递归下去到头

ax + 0*y = gcd(a,0);
所以x=1,y=0;

ax+by=c
如果 d | c 一定有解，否则一定无解

注意1：
exgcd求得是c == d的x,y
x= x * c/d, y = y * c/d;
这里才是正式的ax+by=c的x与y的一组解。

注意2：
exgcd求到得x，可能为负数，所以不断得加最小系数k1和减去k2
a * （ x + k1 ）+ b * ( y - k2 )=d
展开后，保证a * k1= =b * k2 = = lcm(a,b)
所以 k1= lcm(a,b) / a , k2 = lcm(a,b)/b;
然后加成正数就行，但是不是最小正数，x>=k1，就得不断减去k1;

第一步：先求exgcd的，x,y
第二步：看是否需要加系数k1,k2

int exgcd(int a,int b,int &x1,int &y1)///求到c==gcd的一个x与y的解
{
    if(b==0)
    {
        x1=1,y1=0;
        return a;
    }
    int x2,y2;
    int gcd=exgcd(b,a%b,x2,y2);
    x1=y2,y1=x2-a/b*y2;
    return gcd;
}
x=(x%k1+k1)%k1;///这一步才是最小的正整数x，x>=k1，要降，x<0,要增加。

剩余定理

$\left\{ \begin{array}{c} x=a1(mod\ b1) \\ x=a2(mod\ b2) \\ x=a3(mod\ b3) \end{array} \right.$

int mul(int a,int b,int mod)
{
    int res=0;
    while(b>0)
    {
        if(b&1)
            res=(res+a)%mod;
        a=(a+a)%mod;
        b>>=1;
    }
    return res;
}

int exgcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1;
        y=0;
        return a;
    }
    int gcd=exgcd(b,a%b,x,y);
    int tp=x;
    x=y;
    y=tp-a/b*y;
    return gcd;
}

int CRT(vector<int> &A,vector<int> &B,int n)
{
    int x,y,k;
    int mod=B[0],ans=A[0];//第一个方程的解特判
    for(int i=1; i<n; i++)
    {
        int a=mod,b=B[i],c=(A[i]-ans%b+b)%b;//ax≡c(mod b)
        int gcd=exgcd(a,b,x,y),bg=b/gcd;
        if(c%gcd!=0)
            return -1; //判断是否无解，然而这题其实不用
        x=mul(x,c/gcd,bg);
        ans+=x*mod;//更新前k个方程组的答案
        mod*=bg;//M为前k个m的lcm
        ans=(ans%mod+mod)%mod;
    }
    return (ans%mod+mod)%mod;
}

多项式

在数学中，由若干个单项式相加组成的代数式叫做多项式（若有减法：减一个数等于加上它的相反数）。多项式中的每个单项式叫做多项式的项，这些单项式中的最高项次数，就是这个多项式的次数。其中多项式中不含字母的项叫做常数项。

本原多项式

在这里插入图片描述
高斯引理：本原多项式的乘积还是本原多项式。
（证明就算了吧，我不配）

组合数

N=p1^e1 * p2^e2 * p3^e3
N 的因子个数=（1+e1）* ( 1+e2) * (1+e3);
n个不同物品的排列数A（n,n）=A!（原理：加法原理+乘法原理）
公式：A（n,n）=n*（n-1)(n-2)···(n-n+1)=A!
变形一下：
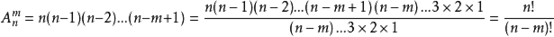
在这里插入图片描述

从n个不同物品取m个的排列数：A（n,m）
公式：A（n,m）=n*（n-1）*(n-2）···（n-m+1）;

从n个不同物品取m个的组合数：C（n,m）
公式：C（n,m）=A（n,m）/A(m,m)=n!/(n-m)!/m!;
这里提一下A(n,m)=P(n,m)，只不过P是老版教材的用法
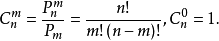
在这里插入图片描述
$C^m_n=\frac{n!}{m!*(n-m)!}$
递推公式：
$C^m_n=C^m_{n-1}+C^{m-1}_{n-1}$
性质1：
$C^m_n=C^{n-m}_n$
性质2：
$C^m_{n+m+1}=\sum^m_{i=0}{C^i_{n+i}}$
性质3：
$C^m_n *C^r_m=C^{r}_n *C^{m-r}_{n-r}$
性质4：（二项式定理）
$\sum^n_{i=0}{C^i_n}=2^n$
性质5：（n为奇数，产生偶数个）
$C^0_n-C^1_n+C^2_n-C^3_n……C^n_n=0$
性质6：（根据性质4和性质5，并且m为奇数）
$C^0_n+C^2_n+C^4_n……=C^1_n+C^3_n+C^5_n……=2^{n-1}$
性质7：
$C^r_{n+m}=C^0_n*C^r_m+C^1_n*C^{r-1}_m……+C^r_n*C^0_m$
性质8：
$m*C^m_n=n*C^{m-1}_{n-1}$
性质9：
$\sum^n_{i=1}{C^i_n*i}=n*2^{n-1}$
性质10：
$\sum^n_{i=1}{C^i_n*i^2}=n*(n+1)*2^{n-2}$
性质11：
$\sum^n_{i=0}{(C^i_n)^2}=C^n_{2n}$
卢卡斯定理
$C^m_n \%p=C^{m/p}_{n/p}*C^{m\%p}_{n\%p} \%p，无脑递归就行$

杨辉三角——数据n<=1e3，时间空间复杂度O（1e6）

#define int long long
const int Clen=2e3+5;
const int mod=998244353;
int C[Clen][Clen];//C[总范围][小范围]
void getC()//数据要预处理
{
    for(int i=0;i<Clen;i++)
    {
        for(int j=0;j<=i;j++)
        {
            if(j==0||j==i)
                C[i][j]=1;
            else
                C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
        }
    }
}

LUCAS定理（留一手，大杀器）

Lucas定理是用于处理特大组合数取模的定理
通常用于解决阶乘无法解决的问题。
在这里插入图片描述

int Lucas(int n, int m)
{
   if(m==0)
       return 1;
   return C(n%mod,m%mod)*Lucas(n/mod,m/mod)%mod;
}

费马小定理——n<=1e6

（乘法逆元+快速幂+阶乘预处理）
预处理O(nlogn)
C(n,m)-O(1)

int fac[N],fac_inv[N];
int fpow(int a,int b)
{
    int ans=1;
    while(b)
    {
        if(b&1)
            ans=ans*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return ans;
}
int C(int n,int m)
{
    if(n<m|m<0)
        return 0;
    return fac[n]*fac_inv[m]%mod*fac_inv[n-m]%mod;
}
void init()
{
    fac[0]=1;
    for(int i=1;i<N;i++)
	    fac[i]=fac[i-1]*i%mod; 
    for(int i=0;i<N;i++)
	    fac_inv[i]=fpow(fac[i],mod-2);
}

插空法（处理不相邻问题）

插空法就是对于解决某几个元素要求不相邻的问题时，先将其他元素排好，再将所指定的不相邻的元素插入它们的间隙或两端位置。首要特点就是不相邻。

例题1：
把1，2，3，4，5组成没有重复数字且数字 1，2不相邻的五位数，则所有不同排法有多少种？
解析：本题直接解答较为麻烦，因为可先将 3，4，5三个元素排定，共有A（3，3）种排法，然后再将 1，2插入四个空位共有A（4，2）种排法，故由乘法原理得，所有不同的五位数有A(3,3)*A(4,2)=72种。

捆绑法（处理相邻问题）

所谓捆绑法，指在解决对于某几个元素要求相邻问题时，先整体考虑，将相邻元素视作一个整体参与排序，然后再单独考虑这个整体内部各元素间顺序。注意：其首要特点是相邻，其次捆绑法一般都应用在不同物体的排序问题中。
例题3：
6个不同的球放到5个不同的盒子中，要求每个盒子至少放一个球，一共有多少种方法?
解答：根据题目要求，则其中一个盒子必须得放 2 个，其他每个盒子放 1 个球，所以从 6 个球中挑出 2 个球看成一个整体，则有C（6，2），这个整体和剩下 4 个球放入 5 个盒子里，则有A（5，5）。方案数：C（6，2）*A（5，5）=1800。

隔板法（处理相同元素+不同分组每组至少存在Si个）

基本题型
基本题型为：n个相同元素，不同个m组，每组至少有一个元素；则只需在 n 个元素的n-1 个间隙中放置 m-1 块隔板把它隔成 m 份，求共有多少种不同方法？

其解题思路为：将 n 个相同的元素排成一行， n 个元素之间出现了（ n-1 ）个空档，现在我们用（ m-1 ）个 “档板 ”插入（ n-1 ）个空档中，就把 n 个元素隔成有序的 m 份，每个组依次按组序号分到对应位置的几个元素（可能是 1 个、2 个、 3 个、 4 个、 ….），这样不同的插入办法就对应着 n 个相同的元素分到 m 组的一种分法，这种借助于这样的虚拟 “档板 ”分配元素的方法称之为插板法。

例题4：
共有 10 完全相同的球分到 7 个班里，每个班至少要分到一个球，问有几种不同分法？
解析：我们可以将 10 个相同的球排成一行， 10 个球之间出现了 9 个空隙，现在我们用 6 个档板 ”插入这 9个空隙中，就 “把 10 个球隔成有序的 7 份，每个班级依次按班级序号分到对应位置的几个球（可能是 1 个、2 个、 3 个、 4 个），这样，借助于虚拟 “档板 ”就可以把 10 个球分到了 7 个班中。
基本题型的变形
（1）变形1：有 n 个相同的元素，要求分到 m 组中，问有多少种不同的分法？
解题思路：这种问题是允许有些组中分到的元素为 “0”，也就是组中可以为空的。对于这样的题，我们就首先将每组都填上 1 个，这样所要元素总数就 m 个，问题也就是转变成将（ n+m ）个元素分到 m 组，并且每组至少分到一个的问题，也就可以用插板法来解决。

例题：有 8 个相同的球放到三个不同的盒子里，共有C（7，2）种不同方法。

解答：题目允许盒子有空，则需要每个组添加 1 个，则球的总数为 8+3 ×1=11，此题就有 C（10 ，2） =45（种）分法了。

（2）变形2：有 n 个相同的元素，要求分到 m 组，要求各组中分到的元素至少某个确定值 S（ s>1，且每组的 s值可以不同），问有多少种不同的分法？

解题思路：这种问题是要求组中分到的元素不能少某个确定值 s，各组分到的不是至少为一个了。对于这样的题，我们就首先将各组都填满，即各组就填上对应的确定值 s 那么多个，这样就满足了题目中要求的最起码的条件，之后我们再分剩下的球。这样这个问题就转变为上面提到的变形1的问题了，也就可以用插板法来解决。

排列组合问题编辑
排列组合问题从解法看，大致有以下几种：
(1)有附加条件的排列组合问题，大多需要分类讨论的方法，注意分类时应不重不漏；
(2)排列与组合的混合型问题，用分类加法或分步乘法计数原理解决；
(3)元素相邻，可以看作是一个整体的方法；
(4)元素不相邻，可以利用插空法；
(5)间接法，把不符合条件的排列与组合剔除掉；
(6)穷举法，把不符合条件的所有排列或组合一一写出来

埃式筛

埃式筛----O（nlog log n）n=2e7 loglon(n)=2.8,也就二倍多一点，大胆去冲.，T了再优化，后悔就来不及了
核心：枚举每个数所有因子

const int N=6.5e4+5;
int a[N];
bool prime[N];///判断该位置是否为素数（素数==ture 非素数=false）
void get_prime()
{
    for(int i=2; i<N; i++) ///埃式筛原理
    {
        if(a[i])
            continue;
        prime[i]=true;
        for(int j=i; j<N; j+=i)
            a[j]=true;
    }
}

欧拉筛----O（n）

核心：
确定为合数：根据最小质因子确定的（仅仅确定一次）——O（2n）
第一个n遍历，第二个n是确定合数
避免确定合数两次，第二次i%it==0得break;
举例：8以内质数存在2 3 5，我们只需要确定28为合数，3*8不用，因为不是由最小合数确定的。后面，就更不用举例了，最小合数都是2了，

vector<int>prime;
bool vis[N];//该位置是否为素数
void get_prime()
{
    for(int i=2;i<N;i++)
    {
        if(vis[i]==0)
            prime.pb(i);
        for(auto it:prime)
        {
            if(it*i>=N)
                break;
            vis[it*i]=true;
            if(i%it==0)
                break;
        }
    }
}

大素数应用（针对1e18以内）

MillerRabin素数测试+Pollard Rho大数质因数分解算法

学习链接
期望时间复杂度 O（n^1/4）,一般比这个还要快
srand(time(0)),记得设置种子
说明：
1：MillerRabin判断一个数是否为素数
2：Pollard Rho得到随机数的因子
code解释：

bool MR(x)		MillerRabin算法，素数判断
int find(x)		Pollard-Rho算法，获得随机因子
int PR(x)		PR递归因子分解，递归随机因子，每个PR()就是一个因子

struct PM
{
    PM()
    {
        srand(time(0));
    }
    int MUL(int a,int b,int p) //a*b%p
    {
        int x=(long double)a/p*b;
        return ((ull)a*b-(ull)x*p+p)%p;
    }
    int POW(int a,int b,int p) //a^b%p
    {
        if(!b)
            return 1;
        if(b==1)
            return a;
        int sum=POW(a,b/2,p);
        if(b%2)
            return MUL(MUL(sum,sum,p),a,p);
        return MUL(sum,sum,p);
    }
    int f(int x,int c,int p)
    {
        return (MUL(x,x,p)+c)%p;
    }
    ///MillerRabin算法，素数判断
    bool MR(int x)
    {
        if(x==0||x==1)
            return false;
        if(x==2)
            return true;
        if(x%2==0)
            return false;
        int p=x-1,q=0;
        while(p%2==0)
            q++,p/=2;
        for(int i=1; i<=10; i++)
        {
            int a=rand()%(x-1)+1;
            if(POW(a,x-1,x)!=1)
                return false;
            int lst=1;
            for(int j=0; j<q; j++)
            {
                int t=POW(a,(1ll<<j)*p,x);
                if(t==1&&lst!=1&&lst!=x-1)
                    return false;
                lst=t;
            }
            if(lst!=1&&lst!=x-1)
                return false;
        }
        return true;
    }
    ///Pollard-Rho算法，获得随机因子
    int find(int x)
    {
        if(x%2==0)
            return 2;
        if(MR(x))
            return x;
        int t=rand()%(x+1);
        int a=t,b=t;
        int c=rand()%(x+1);
        while(1)
        {
            a=f(a,c,x),b=f(f(b,c,x),c,x);
            int d=__gcd(abs(a-b),x);
            if(d>1&&d<x)
                return d;
            if(a==b)
                return find(x);
        }
    }
    ///PR递归因子分解，递归随机因子，每个PR()就是一个因子
    int PR(int x)
    {
        if(x<=1)
            return 1;
        if(MR(x))
            return x;
        int y=find(x);
        return max(PR(y),PR(x/y));
    }
};

数论分块

$\sum_{i=1}^n n/i$
一般问题：n=1e12，O（ $2\sqrt n$ ）
方便理解code

    long long sum=0,n;
    cin>>n;
    for(int l=1,r;l<=n;l=r+1)
    {
        r=n/(n/l);
        sum+=(r-l+1)*(n/l);
    }
    cout<<sum<<endl;

板子

int get(int n,int R)
{
    int sum=0;
    if(R<1)
        return 0;
    R=min(R,n);
    for(int l=1,r;l<=n;l=r+1)
    {
        r=n/(n/l);
        r=min(r,R);
        sum+=(r-l+1)*(n/l);
        if(r==R)
            break;
    }
    return sum;
}

矩阵快速幂

在这里插入图片描述
斐波那契数列前n项和
$f [n] = f [n - 1] + f [n - 2]$
$p r e [n] = p r e [n - 1] + f [n]$
$p r e [n] = f [n + 2] - 1$

1：单位矩阵
2：初始矩阵

const int mod=998244353;
struct matrix
{
    int G[2][2];
};
matrix mul(matrix a,matrix b)
{
    matrix ans;
    memset(ans.G,0);
    for(int i=0; i<2; i++)
        for(int j=0; j<2; j++)
            for(int k=0; k<2; k++)
                ans.G[i][j]=(ans.G[i][j]+a.G[i][k]*b.G[k][j]%mod)%mod;
    return ans;
}
matrix in_pow(matrix a,int b)
{
    matrix ans;
    ans.G[0][0]=1,ans.G[0][1]=0;
    ans.G[1][0]=0,ans.G[1][1]=1;
    while(b)
    {
        if(b&1)
            ans=mul(ans,a);
        a=mul(a,a);
        b>>=1;
    }
    return ans;
}
int mypow(matrix a,int n,matrix c)
{
    return mul(in_pow(a,n),c).G[1][0];
}

博弈

nim模型

模型： n堆物品，每堆有 ai个，两个玩家轮流取走任意一堆的任意个物品，但不能不取。

取走最后一个物品的人获胜。
nim和=sg(a1)^ sg(a2) ^ ……^ sg(an)

sg函数

对于状态 x和它的所有 y1,y2,y3……个后继状态，定义SG 函数：
SG（x）=mex（ SG(y1)，SG(y2),……）；
先确定所有终态

如果终态为lose,则mex所有后继状态
如果终态为win,则mex后继状态，避开所有的终态

高精度

大数整型+ - * % 板子随便用

string delete_leading0(string a)//处理前导0
{
    while(a.size()>1&&a[0]=='0')
        a.erase(a.begin());
    return a;
}
int cmp(string a,string b)//字符串比较大小
{
    a=delete_leading0(a);
    b=delete_leading0(b);
    int len_a=a.size(),len_b=b.size();
    if(len_a<len_b||(len_a==len_b&&a<b))
        return -1;
    if(len_a>len_b||(len_a==len_b&&a>b))
        return 1;
    return 0;
}
string add(string a,string b)//大数加法
{
    a=delete_leading0(a);
    b=delete_leading0(b);
    if(a.size()<b.size())
        swap(a,b);
    string ans;
    reverse(a.begin(),a.end());
    reverse(b.begin(),b.end());
    int len_a=a.size(),len_b=b.size(),sum=0;
    for(int i=0; i<len_a; i++)
    {
        if(i<len_b)
            sum+=a[i]+b[i]-'0'*2;
        else
            sum+=a[i]-'0';
        ans.push_back(sum%10+'0');
        sum/=10;
    }
    if(sum)
        ans.push_back(sum+'0');
    reverse(ans.begin(),ans.end());
    return ans;
}
string sub(string a,string b)//大数减法
{
    int flag=0;
    if(cmp(a,b)<0)
        swap(a,b),flag=1;
    for(int i=a.size()-1,j=b.size()-1; i>=0; i--,j--)
    {
        a[i]=a[i]-(j>=0?b[j]-'0':0);
        if(a[i]<'0')
        {
            a[i]+=10;
            a[i-1]--;
        }
    }
    while(a.size()>1&&a[0]=='0')
        a.erase(a.begin());
    if(flag)
    {
        reverse(a.begin(),a.end());
        a.push_back('-');
        reverse(a.begin(),a.end());
    }
    return a;
}
int bignum_mod(string a,int mod)//大数求余
{
    int sum=0,len=a.size();
    for(int i=0; i<len; i++)
        sum=(sum*10+a[i]-'0')%mod;
    return sum;
}
string div(string str,int b,int &k)
{
    string ans;
    str=delete_leading0(str);
    k=0;//保存余数
    for(auto it:str)
    {
        k=k*10+it-'0';
        ans+='0'+k/b;
        k%=b;
    }
    return delete_leading0(ans);
}
string mul(string a,string b)//大数乘法
{
    a=delete_leading0(a);
    b=delete_leading0(b);
    int la=a.size(),lb=b.size();
    vector<int> ans(la+lb+1);
    string s;
    for(int i=0; i<la; i++)
        for(int j=0; j<lb; j++)
            ans[i+j+1]+=(a[i]-'0')*(b[j]-'0');
    for(int i=la+lb-1; i>0; i--)
    {
        ans[i-1]+=ans[i]/10;
        ans[i]%=10;
    }
    for(int i=0; i<=la+lb-1; i++)
    {
        if(i==0&&ans[i]>0)
            s.push_back(ans[i]+'0');
        if(i)
            s.push_back(ans[i]+'0');
    }
    s=delete_leading0(s);
    return s;
}

备用运算符号重载

struct Big
{
    string str;
    Big(string _str="0")
    {
        str=_str;
    }
    void input()
    {
        cin>>str;
    }
    void output()
    {
        cout<<str<<endl;
    }
    bool operator==(const Big &b)const
    {
        return cmp(str,b.str)?false:true;
    }
    bool operator<(const Big &b)const
    {
        return cmp(str,b.str)<0?true:false;
    }
    bool operator>(const Big &b)const
    {
        return cmp(str,b.str)>0?true:false;
    }
    Big operator+(const Big &b)const
    {
        return add(str,b.str);
    }
    Big operator*(const Big &b)const
    {
        return mul(str,b.str);
    }
    Big operator-(const Big &b)const
    {
        return sub(str,b.str);
    }
};

欧拉函数

巨佬博客学习
单点筛[1,n]与n互质的个数
$O（\sqrt{n}）\phi{(n)}$

int get_phi(int  x){
    int res=x;
    for(int i=2;i*i<=x;i++)
    {
        if(x%i==0){
            res=res-res/i;
            while(x%i==0) x/=i;
        }
    }
    if(x!=1) res=res-res/x;
    return res;
}

埃式筛欧拉函数 $O （ n l o g n ）$

struct aishi_phi///nlogn
{
    vector<int>p;
    aishi_phi(int n)
    {
        p.resize(n);
        for(int i=1;i<n;i++)
            p[i]=i;
        for(int i=2;i<n;i++)
        {
            if(p[i]==i)
            {
                for(int j=i;j<n;j+=i)
                    p[j]=p[j]/i*(i-1);
            }
        }
    }
};

欧拉筛欧拉函数 $O （ n ）$

struct euler_phi
{
    vector<int>p,prime,vis;
    euler_phi(int n)
    {
        p.resize(n+1);
        vis.resize(n+1);
        p[1]=1;
        for(int i=2;i<=n;i++)
        {
            if(!vis[i])
            {
                prime.pb(i);
                p[i]=i-1;
            }
            for(auto it:prime)
            {
                if(it*i>n)
                    break;
                vis[it*i]=true;
                if(i%it==0)
                {
                    p[i*it]=p[i]*it;
                    break;
                }
                else
                    p[i*it]=p[i]*p[it];
            }
        }
    }
};

莫比乌斯

$\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j)==prime]$ max(n,m)<=1e7
init $O （ n ）$
solve $O(\sqrt{n})$
如果 $\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j)==1]$

/*for (int i=1; i<=cnt; i++)
        for (int j=1; prime[i]*j<N; j++)
            f[j*prime[i]]+=mu[j];*/
    for (int i=1; i<N; i++)
        sum[i]=sum[i-1]+mu[i];

const int N=1e7+5;
int mu[N];
int flag[N],prime[N],cnt,f[N],sum[N];
void init()
{
    mu[1]=1;
    for (int i=2; i<N; i++)
    {
        if (!flag[i])
            prime[++cnt]=i,mu[i]=-1;
        for (int j=1; j<=cnt&&i*prime[j]<N; j++)
        {
            flag[i*prime[j]]=1;
            if (i%prime[j]==0)
                break;
            mu[i*prime[j]]=-mu[i];
        }
    }
    for (int i=1; i<=cnt; i++)
        for (int j=1; prime[i]*j<N; j++)
            f[j*prime[i]]+=mu[j];
    for (int i=1; i<N; i++)
        sum[i]=sum[i-1]+f[i];
}
int solve(int a,int b)
{
    int ans=a*b;
    if (a>b)
        swap(a,b);
    for (int l=1,r=0; l<=a; l=r+1)
    {
        r=min(a/(a/l),b/(b/l));
        ans-=(sum[r]-sum[l-1])*(a/l)*(b/l);
    }
    return ans;
}

min_25筛

真正用法：求解积性函数 $f (x)$ 前缀和。
挖个坑，以后再补
时间复杂度：O( $\frac{n^{\frac{3}{4}}}{logn}$ )
非线性筛1e10质数前缀和， $p r i m e$ 数组存1e10数组所有质数。0.05s计算出来，记得每次使用初始化

typedef long long ll;
struct Min25 {

    static const int N=1e6+10;
    ll prime[N], id1[N], id2[N], flag[N], ncnt, m;

    ll g[N], sum[N], a[N], T, n;

    inline int ID(ll x) {
        return x <= T ? id1[x] : id2[n / x];
    }

    inline ll calc(ll x) {
        return x * (x + 1) / 2 - 1;
    }

    inline ll f(ll x) {
        return x;
    }
    inline void Init() {
        memset(prime, 0, sizeof(prime));
        memset(id1, 0, sizeof(id1));
        memset(id2, 0, sizeof(id2));
        memset(flag, 0, sizeof(flag));
        memset(g, 0, sizeof(g));
        memset(sum, 0, sizeof(sum));
        memset(a, 0, sizeof(a));
        ncnt = m = T = n = 0;
    }
    inline void init() {
        T = sqrt(n + 0.5);
        for (int i = 2; i <= T; i++) {
            if (!flag[i]) prime[++ncnt] = i, sum[ncnt] = sum[ncnt - 1] + i;
            for (int j = 1; j <= ncnt && i * prime[j] <= T; j++) {
                flag[i * prime[j]] = 1;
                if (i % prime[j] == 0) break;
            }
        }
        for (ll l = 1; l <= n; l = n / (n / l) + 1) {
            a[++m] = n / l;
            if (a[m] <= T) id1[a[m]] = m; else id2[n / a[m]] = m;
            g[m] = calc(a[m]);
        }
        for (int i = 1; i <= ncnt; i++)
            for (int j = 1; j <= m && (ll)prime[i] * prime[i] <= a[j]; j++)
                g[j] = g[j] - (ll)prime[i] * (g[ID(a[j] / prime[i])] - sum[i - 1]);
    }

    inline ll solve(ll x) {
        if (x <= 1) return x;
        return n = x, init(), g[ID(n)];
    }

}a;

高斯消元（处理线性方程组）

const int N=1e2+5;
double a[N][N],ans[N];
signed main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;++i)
        for(int j=1;j<=n+1;++j)
            cin>>a[i][j];
    for(int i=1;i<=n;++i) //枚举列（项）
    {
        int maxn=i;
        for(int j=i+1;j<=n;++j) //选出该列最大系数
            if(fabs(a[j][i])>fabs(a[maxn][i]))
                maxn=j;
        for(int j=1;j<=n+1;++j) //交换
            swap(a[i][j],a[maxn][j]);
        if(!a[i][i])//最大值等于0则说明该列都为0，肯定无解
        {
            puts("No Solution");
            return 0;
        }
        for(int j=1;j<=n;++j) //每一项都减去一个数（即加减消元）
        {
            if(i==j)
                continue;
            double temp=a[j][i]/a[i][i];
            for(int k=i+1; k<=n+1; ++k)
                a[j][k]-=a[i][k]*temp;
        }
    }
    decimal(2);
    for(int i=1;i<=n;i++)
    {
        ans[i]=a[i][n+1]/a[i][i];
        cout<<ans[i]<<" \n"[i==n];
    }
    return 0;
}

玛咖二锅头

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
数论——板子

数论欧几里得算法证明 O（ logn ）gcd求A和B的最大公约数假设X为最大公约数间接条件：X | A X | B假设A >= B建立方程式A + KB = C = A % B∵ X | A X | KB∴ X | A + KB∴ X | C∴ GCD（A,B）== GCD（B, A%B）然后我们就可以不断的往下辗转相除求GCD（B,C）B和C最大公约数也是X何时是个头GCD（KX , X ）其实这里能被整除，就已经知道求到GCD了再往下GCD （X ,
复制链接

扫一扫