数据结构之二叉查找树（二叉搜索树）

于 2023-01-05 00:24:47 发布
阅读量304 收藏
点赞数
分类专栏： 从头来过 文章标签： 数据结构 图论 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_44230780/article/details/128549044
版权
本文详细介绍了二叉查找树的概念，包括其定义、创建过程、中序遍历、查找和删除操作。通过示例代码展示了如何插入、查找和删除元素，帮助理解二叉查找树的工作原理。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

从头来过之数据结构二叉查找树

二叉查找树（二叉搜索树）

可能是空树
或者满足以下条件
1、若左子树存在，则左子树结点值小于根结点值
2、若右子树存在，则右子树结点值大于根结点值
3、且左右子树皆是二叉查找树

创建二叉查找树

使用的结点值为54、20、66、40、28、79、58
将这些数据依次插入，创建二叉查找树

可以点击此处动态实现一下 依次输入上述的值 进行插入建树

创建出的查找二叉树

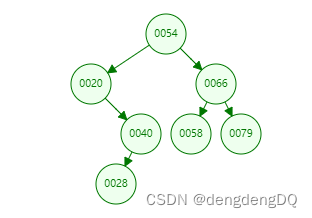
在这里插入图片描述

开始建树

定义树结点的结构体


//20230104 二叉排序树（二叉查找树）

//创建二叉查找树
typedef int ElemType;
//树的根节点的结构体
typedef struct STNode {
	ElemType data;//用来存放数据域
	STNode* Lchild, * Rchild;//用来指向该结点的左右结点
}STNode,*STree;

建树

//创建二叉树的函数
void creat_STree(STree& tree, ElemType str[], int len) {
	//因为要对树进行改变，所以使用引用
	tree = NULL;
	int i=0;//方便遍历数组 取出数据 进行插树
	while (i <len) {
		insert(tree, str[i]);//调用插入树元素函数
		i++;
	}
}

像树中插入元素的函数insert
此处使用递归思想：
当像树中插入元素时
若为空树，则创建根节点，并将值存入即可
若不为空树，则要进行比较大小
若存入数据元素比根结点元素小，则须将该元素与根结点的左结点进行比较（左结点为空存入 不为空 在与左结点比较 大于存左结点的右结点，小于存左结点的左结点）递归思想
若存入数据元素比根结点元素大，则须将该元素与根结点的右结点进行比较（右结点为空存入 不为空 在与右结点比较 大于存右结点的右结点，小于存右结点的左结点）递归思想

//在树中进行插入的函数(使用递归思想)
void insert(STree& p, ElemType i) {
	if (NULL == p) {
		p = (STree)malloc(sizeof(STNode));//为根节点申请空间
		//根为空，将元素放入该结点
		p->data = i;
		p->Lchild = NULL;
		p->Rchild=NULL;
	}
	else if (i < p->data) {
		//插入元素小于根节点元素 将其插入左子树
		insert(p->Lchild, i);
	}
	else {
		//插入元素大于根节点元素，将其插入右子树
		insert(p->Rchild, i);
	}

}

对新建的二叉查找树进行中序遍历

//使用中序遍历（左根右） 进行打印（得出的二叉查找树结果应为从小到大）
void inOrder(STree tree) {
	if (tree != NULL) {
		inOrder(tree->Lchild);
		printf("%3d", tree->data);
		inOrder(tree->Rchild);
	}

}

主函数代码

STree tree = (STree)malloc(sizeof(STNode));//为树结点指针向内存申请指向空间（地址）
	ElemType str[] = { 54,20,66,40,28,79,58 };//要创建的树的值
	int len = 7;//加入的总结点个数
	creat_STree(tree, str, len);//创建二叉排序树的函数
	inOrder(tree);//中序遍历二叉排序树

中序遍历二叉查找树结果

将二叉查找树从小到大输出 因为中序遍历是 左根右
二叉查找树也满足 左子树<根<右子树
在这里插入图片描述

二叉搜索数的查找

先将要查找元素与根结点进行比较 相等返回根结点
不等 比根结点大 和根结点的右结点进行比较 （重复相等返回 不等 在按大小 与左右结点比较）比根节点小 与根结点的左结点比较

只找到被查找元素的代码

//查找对应的元素并传回

int search_elem_in_STree(STree tree, ElemType elem, STree& parent) {
	//parent使用引用是因为如果查找到对应的元素则将结点地址赋予parent
	STree p = tree;
	while (NULL != p) {
		if (elem == p->data) {
			parent = p;
			return 1;//表示查找到当前元素
		}
		else if (elem > p->data) {
			//当前元素比根结点元素大 将该元素与根结点的右结点进行比较查找
			p = p->Rchild;
		}
		else {
			//当前元素比根结点元素小，将该元素与根结点的左结点进行比较查找
			p = p->Lchild;
		}
	}
	return 0;//表示没有查到指定元素
}

查找结果时同时返回该元素的父节点值（有助于删除操作）

函数返回值为查找到的元素所在结点
元素所在结点的父结点值通过引用的方式在函数内部进行了传递

//查找对应的结点返回 并传回其父结点
STree search_elem_in_STree(STree tree, ElemType elem, STree& parent) {
	//parent使用引用是因为如果查找到对应的元素则将结点的父结点地址赋予parent
	parent = NULL;
	while (NULL != tree && elem != tree->data) {
		parent = tree;
		if (elem < tree->data)
			tree = tree->Lchild;
		else tree = tree->Rchild;
	}
	return tree;//返回查找到的对应元素结点
}

主函数代码

STree parent;//用来接查找到的元素的父亲结点
	STree search=search_elem_in_STree(tree, 40, parent);//查找对应元素并传回
	if (search) {
		printf("找到对应结点，其值为%d\n", search->data);
	}
	else {
		printf("没有找到对应元素\n");
	}

二叉查找树查找结果

在这里插入图片描述

二叉查找树的删除

首先判断该树是否为空 空 则直接返回 不用删除
不为空，则先在树中查找到对应的元素结点
当该结点的左子树为空时，直接将右子树移动到该位置即可 释放要删除的元素结点所占空间
当该结点的右子树为空时，则直接左子树移动到该位置即可 释放要删除元素结点所占空间
左右子树皆不为空时
可以将左子树的最大值结点赋值给要删除元素的结点 再将左子树中的最大值结点删除
或者将右子树的最小值结点赋值给要删除的元素的结点 再将右子树中的最小值结点删除

//二叉查找树 根据元素 删除对应结点
void DeleteNode(STree& tree, ElemType elem) {
	//如果树为空树 则直接返回不用进行删除操作
	if (NULL == tree) {
		return;
	}
	//树不为空
	STree parent;//用于接收查找到的元素结点的父结点
	STree search;//用于接收查找到的元素的元素结点
	search=search_elem_in_STree(tree, elem, parent);//调用查找元素的函数 上面有定义
	STree freeDelete;//用来存储要释放的内存空间地址
	if (search) {
		//此时查找到要删除的元素
		if (search->Lchild == NULL) {
			//如果要删除元素的左结点为空 直接将要删除元素的右结点接到要删除的位置 释放要删除的元素的空间
			freeDelete = search;//指向要删除元素在内存的空间地址
			search = search->Rchild;//将删除元素的右结点移至要删除的位置
			free(freeDelete);//释放掉该指针指向的内存空间 防止别的指针指向该内存空间时 有数据
		}
		else if (search->Rchild == NULL) {
			//如果要删除元素的右结点为空 直接将要删除元素的左结点接到要删除的位置 释放要删除的元素的空间
			freeDelete = search;//指向要删除元素在内存的空间地址
			search = search->Lchild;//将删除元素的左结点移至要删除的位置
			free(freeDelete);//释放掉该指针指向的内存空间 防止别的指针指向该内存空间时 有数据
		}
		else {
			//要删除元素的左右结点都不为空时，可以将左子树的最大结点 或者 右子树的最小结点 移到要删除元素的位置
			//找到要删除结点的左子树中最大值的结点-----------从左子树的根结点起 找其右结点 当右结点为空时 即是
			freeDelete = search->Lchild;
			while (freeDelete->Rchild != NULL) {
				freeDelete = freeDelete->Rchild;
			}
			//循环结束后 此时freeDelete指向的就是要删除数值的结点的左子树中的最大结点
			search->data = freeDelete->data;//将左子树的最大值赋给要删除的数值所在结点
			DeleteNode(search->Lchild, freeDelete->data);//将左子树中的最大值从左子树中删除

		}
	}
}

主函数代码

DeleteNode(tree, 66);
	//inOrder(tree);//再将二叉查找树进行一次中序遍历（从小到大）

全部代码展示


//20230104 二叉排序树（二叉查找树）

//创建二叉查找树
typedef int ElemType;
//树的根节点的结构体
typedef struct STNode {
	ElemType data;//用来存放数据域
	STNode* Lchild, * Rchild;//用来指向该结点的左右结点
}STNode,*STree;
//在树中进行插入的函数(使用递归思想)
void insert(STree& p, ElemType i) {
	if (NULL == p) {
		p = (STree)malloc(sizeof(STNode));//为根节点申请空间
		//根为空，将元素放入该结点
		p->data = i;
		p->Lchild = NULL;
		p->Rchild=NULL;
	}
	else if (i < p->data) {
		//插入元素小于根节点元素 将其插入左子树
		insert(p->Lchild, i);
	}
	else {
		//插入元素大于根节点元素，将其插入右子树
		insert(p->Rchild, i);
	}

}
//创建二叉树的函数
void creat_STree(STree& tree, ElemType str[], int len) {
	//因为要对树进行改变，所以使用引用
	tree = NULL;
	int i=0;//方便遍历数组 取出数据 进行插树
	while (i <= len - 1) {
		insert(tree, str[i]);//调用插入树元素函数
		i++;
	}
}
//使用中序遍历（左根右） 进行打印（得出的二叉查找树结果应为从小到大）
void inOrder(STree tree) {
	if (tree != NULL) {
		inOrder(tree->Lchild);
		printf("%3d", tree->data);
		inOrder(tree->Rchild);
	}

}
//查找对应的元素并传回
//
//int search_elem_in_STree(STree tree, ElemType elem, STree& parent) {
//	//parent使用引用是因为如果查找到对应的元素则将结点地址赋予parent
//	STree p = tree;
//	while (NULL != p) {
//		if (elem == p->data) {
//			parent = p;
//			return 1;//表示查找到当前元素
//		}
//		else if (elem > p->data) {
//			//当前元素比根结点元素大 将该元素与根结点的右结点进行比较查找
//			p = p->Rchild;
//		}
//		else {
//			//当前元素比根结点元素小，将该元素与根结点的左结点进行比较查找
//			p = p->Lchild;
//		}
//	}
//	return 0;//表示没有查到指定元素
//}

//查找对应的结点返回 并传回其父结点
STree search_elem_in_STree(STree tree, ElemType elem, STree& parent) {
	//parent使用引用是因为如果查找到对应的元素则将结点的父结点地址赋予parent
	parent = NULL;
	while (NULL != tree && elem != tree->data) {
		parent = tree;
		if (elem < tree->data)
			tree = tree->Lchild;
		else tree = tree->Rchild;
	}
	return tree;//返回查找到的对应元素结点
}

//二叉查找树 根据元素 删除对应结点
void DeleteNode(STree& tree, ElemType elem) {
	//如果树为空树 则直接返回不用进行删除操作
	if (NULL == tree) {
		return;
	}
	//树不为空
	STree parent;//用于接收查找到的元素结点的父结点
	STree search;//用于接收查找到的元素的元素结点
	search=search_elem_in_STree(tree, elem, parent);//调用查找元素的函数 上面有定义
	STree freeDelete;//用来存储要释放的内存空间地址
	if (search) {
		//此时查找到要删除的元素
		if (search->Lchild == NULL) {
			//如果要删除元素的左结点为空 直接将要删除元素的右结点接到要删除的位置 释放要删除的元素的空间
			freeDelete = search;//指向要删除元素在内存的空间地址
			search = search->Rchild;//将删除元素的右结点移至要删除的位置
			free(freeDelete);//释放掉该指针指向的内存空间 防止别的指针指向该内存空间时 有数据
		}
		else if (search->Rchild == NULL) {
			//如果要删除元素的右结点为空 直接将要删除元素的左结点接到要删除的位置 释放要删除的元素的空间
			freeDelete = search;//指向要删除元素在内存的空间地址
			search = search->Lchild;//将删除元素的左结点移至要删除的位置
			free(freeDelete);//释放掉该指针指向的内存空间 防止别的指针指向该内存空间时 有数据
		}
		else {
			//要删除元素的左右结点都不为空时，可以将左子树的最大结点 或者 右子树的最小结点 移到要删除元素的位置
			//找到要删除结点的左子树中最大值的结点-----------从左子树的根结点起 找其右结点 当右结点为空时 即是
			freeDelete = search->Lchild;
			while (freeDelete->Rchild != NULL) {
				freeDelete = freeDelete->Rchild;
			}
			//循环结束后 此时freeDelete指向的就是要删除数值的结点的左子树中的最大结点
			search->data = freeDelete->data;//将左子树的最大值赋给要删除的数值所在结点
			DeleteNode(search->Lchild, freeDelete->data);//将左子树中的最大值从左子树中删除

		}
	}
}
int main() {
//20230104 新年快乐 💪
	//二叉排序树（二叉查找树）
	
	//二叉排序树可能是一颗空树
	//也可能满足以下条件
	//1、若左子树为空，则左子树所有结点的值都小于根节点的值
	//2、若右子树为空，则右子树的所有结点的值都大于根节点的值
	//3、左右子树也分别是一颗二叉排序树（即：需要满足上述要求）

	//创建一颗二叉排序树
	//存入数据为 54、20、66、40、28、79、58
	
	STree tree = (STree)malloc(sizeof(STNode));//为树结点指针向内存申请指向空间（地址）
	ElemType str[] = { 54,20,66,40,28,79,58 };//要创建的树的值
	int len = 7;//加入的总结点个数
	//大体逻辑： 插入元素 
	//插入第一个元素 判断此时树根是不是为空 ，为空将该元素设置为树根
	//插入第二个元素，判断此时树根是否为空，不为空，判断与树根的大小
	//大于树根 判断其树根的右结点是否为空，为空存入右结点，不为空 继续与树根的右结点比较大小
	//小于树根 判断其树根的左结点是否为空，为空存入左结点，不为空，继续与树根的左结点比较大小
	creat_STree(tree, str, len);//创建二叉排序树的函数
	inOrder(tree);//中序遍历二叉排序树
	printf("\n");
	//大体逻辑：查找元素
	//将查找元素与根元素进行对比 相等返回
	//比根元素大 则继续与根的右结点元素进行比较 （相等返回 大与右结点比较 小与左结点比较）
	//比根元素小 则继续与根的左结点元素进行比较 （相等返回 大与右结点比较 小与左结点比较）
	//对二叉查找树进行查找时 最多查找次数为树的层数
	STree parent;//用来接查找到的元素的父亲结点
	STree search=search_elem_in_STree(tree, 40, parent);//查找对应元素并传回
	if (search) {
		printf("找到对应结点，其值为%d\n", search->data);
	}
	else {
		printf("没有找到对应元素\n");
	}

	//删除元素
	//删除元素时，需要先找到对应元素
	//当要删除元素左子树为空时，直接将删除元素的右子树接到要删除的位置 释放到要删除的空间
	//当要删除元素右子树为空时，直接将删除元素的左子树接到要删除的位置 释放到要删除的空间
	//当要删除元素的左右子树都存在时，将左子树的最大值，或右子树的最小值移到要删除的位置 再将对应的左子树或右子树中的最大值删除
	DeleteNode(tree, 66);
	//inOrder(tree);//再将二叉查找树进行一次中序遍历（从小到大）
 	return 0;
}
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值