python编程作业--盐度对流方程的差分格式设计与讨论

使用python对于盐度对流差分格式设计与讨论

题目要求如下：

差分格式设计如下：

方案1、蛙跳格式（时间和距离都用中央差）

python代码如下：

"""
Created on %(date)s

@author: %(jixianpu)s

Email : 211311040008@hhu.edu.cn

introduction : keep learning althongh walk slowly
"""

"""
分析说明：μ<1时，蛙跃格式是稳定的，但是会有频散现象发生，耗散比较小，盐度场峰值基本保持不变；μ>1时，明显看到格式不稳定。
"""


import numpy as np
import matplotlib.pyplot as plt
ss=np.zeros((2002,1002))   
dx=10
u=1
dt=5
#mu=u*dt/dx;
mu=1.1 #1.01,0.01,0.05
ss[0,300:401]=10
for n  in range(2001):
    for  j in range(1001):
        if (n==1)&(j==1):
            s1=ss[n,j]
            s2=ss[n,j]
            ss[n+1,j]=s1+mu*(-ss[n,j+1]+s2)
        elif n==1 & j!=1:
            s1=ss[n,j]
            ss[n+1,j]=s1+mu*(-ss[n,j+1]+ss[n,j-1])
        elif j==1 &n!=1:
            s2=ss[n,j]
            ss[n+1,j]=ss[n-1,j]+mu*(-ss[n,j+1]+s2)
        else :
            ss[n+1,j]=ss[n-1,j]+mu*(-ss[n,j+1]+ss[n,j-1])
           
plt.rcParams['axes.unicode_minus'] = False
fig=plt.figure(figsize=(15,15))   
ax=fig.add_subplot(1,1,1)
ax.plot(ss[1000])
# ax.set_xlim(0,1000)
# ax.set_ylim(-3,14)
ax.set_xlabel('area range',fontsize=30)
ax.set_ylabel('salinity',fontsize=30)
ax.tick_params(which='major',direction='out', pad=8,labelsize=25,length=10,\
                axis='both',bottom=True, left=True, right=False, top=False)
ax.set_title('t=1000s',fontsize=30)

图片如下：

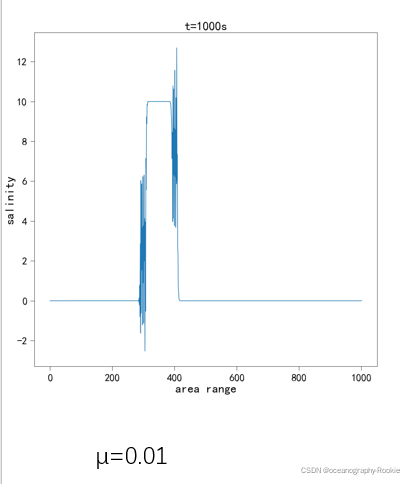
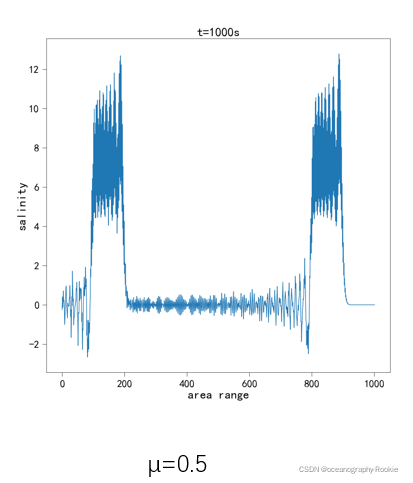
分析结论：

μ<1时，蛙跃格式是稳定的，但是会有频散现象发生，耗散比较小，盐度场峰值基本保持不变；μ>1时，明显看到格式不稳定。

---

方案2、迎风格式（时间用前差，距离用后差）

python 核心代码如下：

for n  in range(2001):
    for  j in range(1001):
        if (j==1):
            s1=ss[n,j]
            ss[n+1,j]=ss[n,j]-mu*(ss[n,j]-s1)
        else :
            ss[n+1,j]=ss[n,j]-mu*(ss[n,j]-ss[n,j-1])

图片如下：

分析结论：

在μ<1时，迎风格式是稳定的，没有发生频散，但是发生耗散，盐柱的棱角变得圆滑。μ>1时，格式变得不稳定。。

---

方案3、欧拉格式（时间用前差，距离用中央差）

python 核心代码：

for n  in range(2001):
    for  j in range(1001):
        if (j==1):
            s1=ss[n,j]
            ss[n+1,j]=ss[n,j]-0.5*mu*(ss[n,j+1]-s1)
        else :
            ss[n+1,j]=ss[n,j]-0.5*mu*(ss[n,j+1]-ss[n,j-1])

图片如下：

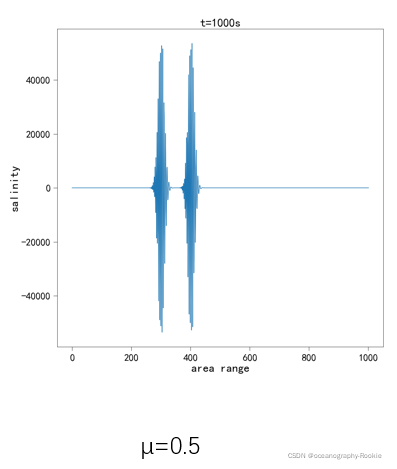
分析结论：

欧拉法是一种绝对不稳定的格式，无论mu取多小，都是不稳定的

---

方案4、lax格式（在欧拉格式右边增加一个耗散项）

python 核心代码：

mu=1.1
miu2=u*u*dt/(dx*dx)
for n  in range(2001):
    for  j in range(1001):
        if (j==1):
            s1=ss[n,j]
            ss[n+1,j]=ss[n,j]-0.5*mu*(ss[n,j+1])+0.5*mu*s1+miu2*ss[n,j+1]-2*miu2*ss[n,j]+miu2*s1
        else :
            ss[n+1,j]=ss[n,j]-0.5*mu*(ss[n,j+1])+0.5*mu*ss[n,j-1]+miu2*ss[n,j+1]-2*miu2*ss[n,j]+miu2*ss[n,j-1]

图片如下：

分析结论：

在μ<1时，此格式是稳定的，有少许频散，耗散也比较少，盐度值是比较稳定的。
在μ>1时，格式不稳定。

ps：代码可能有点粗糙，只是简单记录一下，欢迎评论讨论。

			一个努力学习python的海洋人
            水平有限，欢迎指正！！！
            欢迎评论、收藏、点赞、转发、关注。
            关注我不后悔，记录学习进步的过程~~