城市交通导航最短路径查询

导航最短路径查询系统

上学期期末老师让写一个课程设计，给了很多课题，选了导航最短路径查询系统，题目如下：
1 项目简介

设计一个交通咨询系统，能让旅客咨询从任一个城市顶点到另一个城市顶点之间的最短路径问题。设计分三个部分，一是建立交通网络图的存储结构；二是解决单源最短路径问题；最后再实现两个城市顶点之间的最短路径问题。
最短路径问题的提出随着计算机的普及以及地理信息科学的发展，GIS因其强大的功能得到日益广泛和深入的应用。网络分析作为GIS最主要的功能之一，在电子导航、交通旅游、城市规划以及电力、通讯等各种管网、管线的布局设计中发挥了重要的作用。而网络分析中最基本和关键的问题是最短路径问题。
最短路径不仅仅指一般地理意义上的距离最短，还可以引申到其他的度量，如时间、费用、线路容量等。相应地，最短路径问题就成为最快路径问题、最低费用问题等。由于最短路径问题在实际中常用于汽车导航系统以及各种应急系统等（110报警、119火警以及医疗救护系统），这些系统一般要求计算出到出事地点的最佳路线的时间一般在1s-3s，在行车过程中还需要实时计算出车辆前方的行驶路线，这就决定了最短路径问题的实现应该是高效率的。最优路径问题不仅包括最短路径问题，还有可能涉及到最少时间问题、最少收费（存在收费公路）问题、或者是几个问题的综合，这时将必须考虑道路级别、道路流量、道路穿越代价（如红灯平均等待时间）等诸多因素。但是必须指出的是，一般来说最优路径在距离上应该是最短的，但最短路径在行驶时间和能源消耗的意义上未必是最优的。其实，无论是距离最短、时间最快还是费用最低，它们的核心算法都是最短路径算法。
2 设计思路

单源最短路径算法的主要代表之一是Dijkstra（迪杰斯特拉）算法。该算法是目前多数系统解决最短路径问题采用的理论基础，在每一步都选择局部最优解，以期望产生一个全局最优解。
Dijksira算法的基本思路是：对于图G=(V,E)，V是包含n个顶点的顶点集，E是包含m条弧的弧集，(v, w)是E中从v到w的弧，c(v, w)是弧(v, w)的非负权值，设s为V中的顶点，t为V中可由s到达的顶点，则求解从s至t的具有最小弧权值和的最短路径搜索过程如下：
(1) 将v中的顶点分为3类：已标记点、未标记点、己扫描点。将s初始化为己标记点，其它顶点为未标记点。为每个顶点v都建立一个权值d和后向顶点指针p，并将d初始化如下：d(v)=0，v=s；d(v)=∞，v≠s。
(2) 重复进行扫描操作：从所有已标记点中选择一个具有最小权值的顶点v并将其设为己扫描点，然后检测每个以v为顶点的弧(v, w)，若满足d(v) + c(v, w) < d(w) 则将顶点v设为已标记点，并令d(w) = d(v) + c(v, w), p(w) = v。
(3) 若终点t被设为已扫描点，则搜索结束。由t开始遍历后向顶点指针P直至起点s，即获得最短路径解。
3 数据结构

（1）定义一个数组min_dist，它的每个数组元素min_dist[i]表示当前所找到的从始点vi到每个终点vj的最短路径的长度。它的初态为：若从vi到vj有边，则min_dist[j]为边的权值；否则置min_dist[i]为∞。定义一个数组path，其元素path[k]（0≤k≤n-1）用以记录vi到vk最短路径中vk的直接前驱结点序号，如果vi到vk存在边，则path[k]初值为i。定义一个数组W，存储任意两点之间边的权值。
　 （2）查找min(min_dist[j]，j∈V-S)，设min_dist[k]最小，将k加入S中。修改对于V-S 中的任一点vj，min_dist[j]=min(min_dist[k]+w[k][j], min_dist[j]) 且path[j]=k。
　 （3）重复上一步，直到V-S为空。
　　在算法设计时，用一个tag数组来记录某个顶点是否已计算过最短距离，如果tag[k]=0，则vk∈V-S，否则vk∈S。初始值除tag[i]=1以外，所有值均为0。

路径图如下：
迪杰斯特拉算法流程图如下：

弗洛伊德算法流程图如下：

代码总体结构图如下：

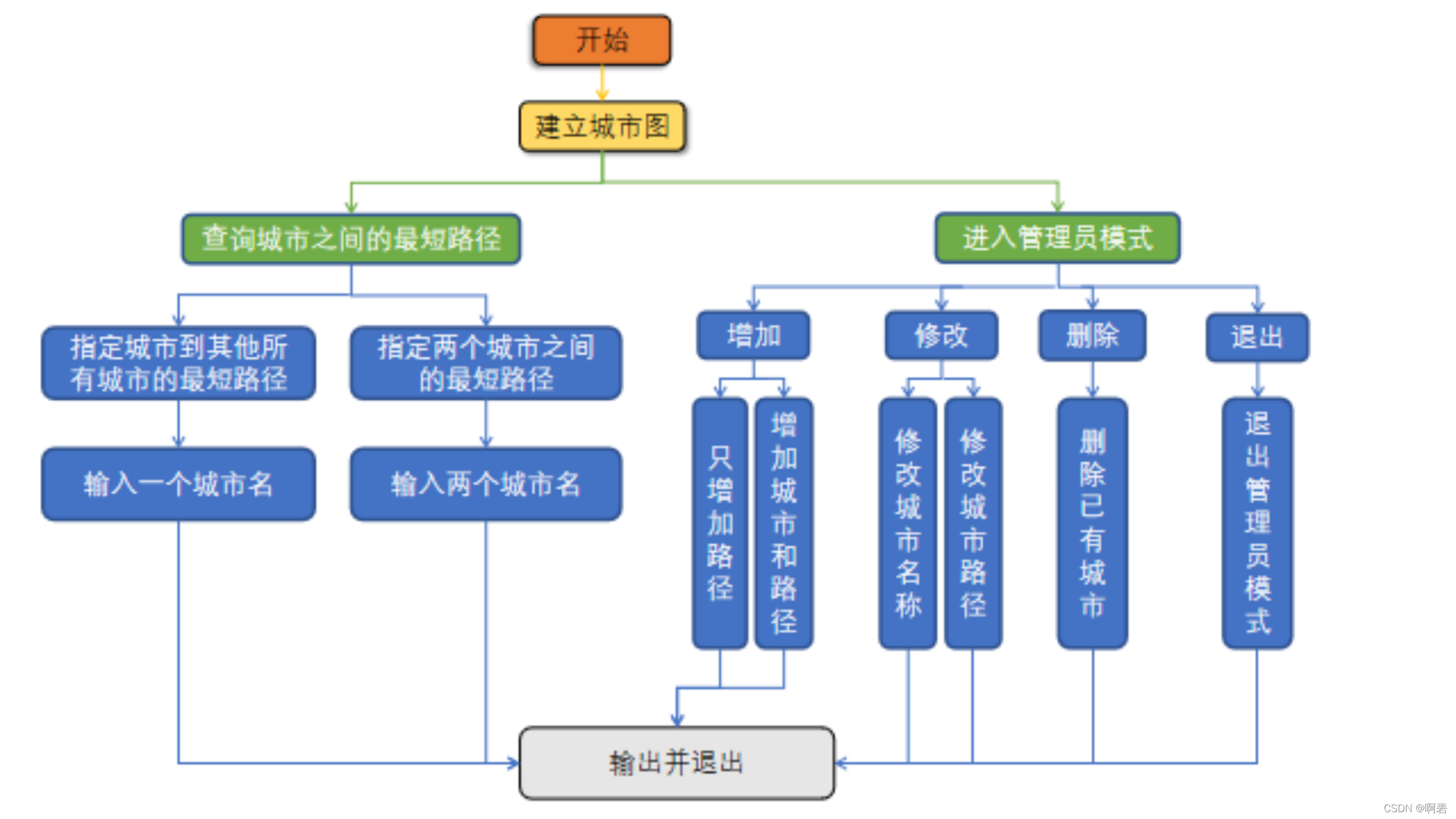
在写代码期间也遇到了好多的问题，反反复复改了好多次，代码如下：

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define INFINITY 50000
#define MAXVERTEX 35
#define NAMESLEN 20
typedef char VRType;
typedef int AdjMatrix;
typedef struct {
   
	VRType city[50]; 
	int id;
}VertexType;
typedef struct{
   
	VertexType vex[MAXVERTEX];//城市
	AdjMatrix arcs[MAXVERTEX][MAXVERTEX];//用于存放城市之间路径的矩阵 
	int vexnum,arcnum;//图中的城市数量和路径的数量 
}Mgraph;	
typedef int Pathmatirx[MAXVERTEX][MAXVERTEX];// 二维数组用于弗洛伊德算法中存放经过的城市的id 
typedef int ShortPathTable[MAXVERTEX][MAXVERTEX];//用于存放最短路径上城市的距离 
typedef enum {
    FALSE, TRUE }boolean;//用来判断跳出管理模式 

int is_exitx(Mgraph G,char city[]);
int Transform_id(Mgraph G,char city[]);
void CreateGraph(Mgraph &G);
void ShortestPath_DIJ(Mgraph G,int v0);
void ShortestPath_FLOYD(Mgraph G,Pathmatirx &P, ShortPathTable &D);
void addPath(Mgraph &G,int anum);
void Traversal(Mgraph &G);
void addCityandPath(Mgraph &G);
void Delete(Mgraph &G);
int modPath(Mgraph &G,int path_s);
void modCity(Mgraph &G);
void System(Mgraph &G);


int is_exitx(Mgraph G,char city[])//判断城市是否存在的方法，存在返回1否则返回0 
{
   
	int flag=0;
	
	for(int i = 0;i<G.vexnum;i++){
   
		if (strcmp(city, G.vex[i].city) == 0)
		{
   
			flag=1;
			break;
		}
	}
	
	return flag;
} 


int Transform_id(Mgraph G,char city[])//获取城市id的函数，后面会频繁用到 
{
   
	int i,id;
	
	for(i=0;i<G.vexnum;i++)
	{
   
		if(strcmp(G.vex[i].city,city)==0)
		{
   
				id=G.vex[i].id;
		}
	}
	
	return id;
} 
	
	
void CreateGraph(Mgraph &G)//创建城市交通图 
{
   
	G.vexnum = 25;	//交通图中初始化城市的数量 
	G.arcnum = 30;  //交通图中初始化路径的数量 
	int a,d,e,f,g,i,j,w,num;
	char b[NAMESLEN],c[NAMESLEN];

	for(i=0;i<G.vexnum;i++)//初始化图的顶点id 
	{
   
		G.vex[i].id=i;
	}
	printf("===============            初始化交通图路线          =================\n");
	strcpy(G.vex[0].city,"郑州");
	strcpy(G.vex[1].city,"北京");
	strcpy(G.vex[2].city,"西安");
	strcpy(G.vex[3].city,"武汉");
	strcpy(G.vex[4].city,"徐州");
	strcpy(G.vex[5].city,"天津");
	strcpy(G.vex[6].city,"呼和浩特");
	strcpy(G.vex[7].city,"兰州");
	strcpy(G.vex[8].city,"成都");
	strcpy(G.vex[9].city,"株洲");
	strcpy(G.vex[10].city,"南昌");
	strcpy(G.vex[11].city,"上海");
	strcpy(G.vex[12].city,"乌鲁木齐");
	strcpy(G.vex[13].city,"西宁");
	strcpy(G.vex[14].city,"昆明");
	strcpy(G.vex[15].city,"贵阳");
	strcpy(G.vex[16].city,"南宁");
	strcpy(G.vex[17].city,"柳州");
	strcpy(G.vex[18].city,"广州");
	strcpy(G.vex[19].city,"深圳");
	strcpy(G.vex[20].city,"福州");
	strcpy(G.vex[21].city,"大连");
	strcpy(G.vex[22].city,"沈阳");
	strcpy(G.vex[23].city,"长春");
	strcpy(G.vex[24].city,"哈尔滨");
	 
	for(i=0;i<G.vexnum;i++)//初始化图矩阵 
	{
   
		for(int j=0;j<G.vexnum;j++)
		{
   
			G.arcs[i][j]=INFINITY;
		}
	}
	 
	G.arcs[0][1] = 695;//郑州-----北京 
	G.arcs[1][0] = 695;
	
	G.arcs[0][2] = 511;//郑州-----西安 
	G.arcs[2][0] = 511;
	
	G.arcs[0][3] = 534;//郑州-----武汉 
	G.arcs[3][0] = 534;
	
	G.arcs[0][4] = 349;//郑州-----徐州 
	G.arcs[4][0] = 349;
	
	G.arcs[1][5] = 137;//北京-----天津