铁路平板车装货问题(用Lingo求解)
有七种规格的包装箱要装到两节铁路平板车上去。包装箱的宽和高是一样的,厚度(t,cm 计)及重量(w,kg计)不同。表1给出了包装箱的厚度、重量以及数量。每节平板车有10.2m 长的地方可装包装箱,载重为40t。由于当地货运的限制,对于C5, C6, C7 类包装箱的总数有一个特别限制:箱子所占的空间(厚度)不能超过302.7cm。试把包装箱装到平板车上,使得浪费空间最小。
| 种类 | C1 | C2 | C3 | C4 | C5 | C6 | C7 |
| t/cm | 48.7 | 53.0 | 61.3 | 72.0 | 48.7 | 52.0 | 64.0 |
| w/kg | 2000 | 3000 | 1000 | 500 | 4000 | 2000 | 1000 |
| n/件 | 8 | 7 | 9 | 6 | 6 | 4 | 8 |

model:
sets:
A/n1..n7/:T,W,N;
B/1,2/;
links(A,B):X;
endsets
max=@sum(A(i):@sum(B(j):X(i,j)*T(i)));
@for(B(j):@sum(A(i):X(i,j)*T(i))<=1020);
@sum(B(j):@sum(A(i)|i#ge#5:X(i,j)*T(i)))<=302.7;
@for(B(j):@sum(A(i):X(i,j)*W(i))<=40000);
@for(A(i):@sum(B(j):X(i,j))<=N(i));
@for(links:@gin(X));
data:
T=48.7 53 61.3 72 48.7 52 64;
W=2000 3000 1000 500 4000 2000 1000;
N=8 7 9 6 6 4 8;
enddata
end
Variable Value Reduced Cost
T( N1) 48.70000 0.000000
T( N2) 53.00000 0.000000
T( N3) 61.30000 0.000000
T( N4) 72.00000 0.000000
T( N5) 48.70000 0.000000
T( N6) 52.00000 0.000000
T( N7) 64.00000 0.000000
W( N1) 2000.000 0.000000
W( N2) 3000.000 0.000000
W( N3) 1000.000 0.000000
W( N4) 500.0000 0.000000
W( N5) 4000.000 0.000000
W( N6) 2000.000 0.000000
W( N7) 1000.000 0.000000
N( N1) 8.000000 0.000000
N( N2) 7.000000 0.000000
N( N3) 9.000000 0.000000
N( N4) 6.000000 0.000000
N( N5) 6.000000 0.000000
N( N6) 4.000000 0.000000
N( N7) 8.000000 0.000000
X( N1, 1) 5.000000 -48.70000
X( N1, 2) 3.000000 -48.70000
X( N2, 1) 2.000000 -53.00000
X( N2, 2) 5.000000 -53.00000
X( N3, 1) 7.000000 -61.30000
X( N3, 2) 2.000000 -61.30000
X( N4, 1) 2.000000 -72.00000
X( N4, 2) 4.000000 -72.00000
X( N5, 1) 2.000000 -48.70000
X( N5, 2) 3.000000 -48.70000
X( N6, 1) 0.000000 -52.00000
X( N6, 2) 1.000000 -52.00000
X( N7, 1) 0.000000 -64.00000
X( N7, 2) 0.000000 -64.00000
点击以下检验

检验符合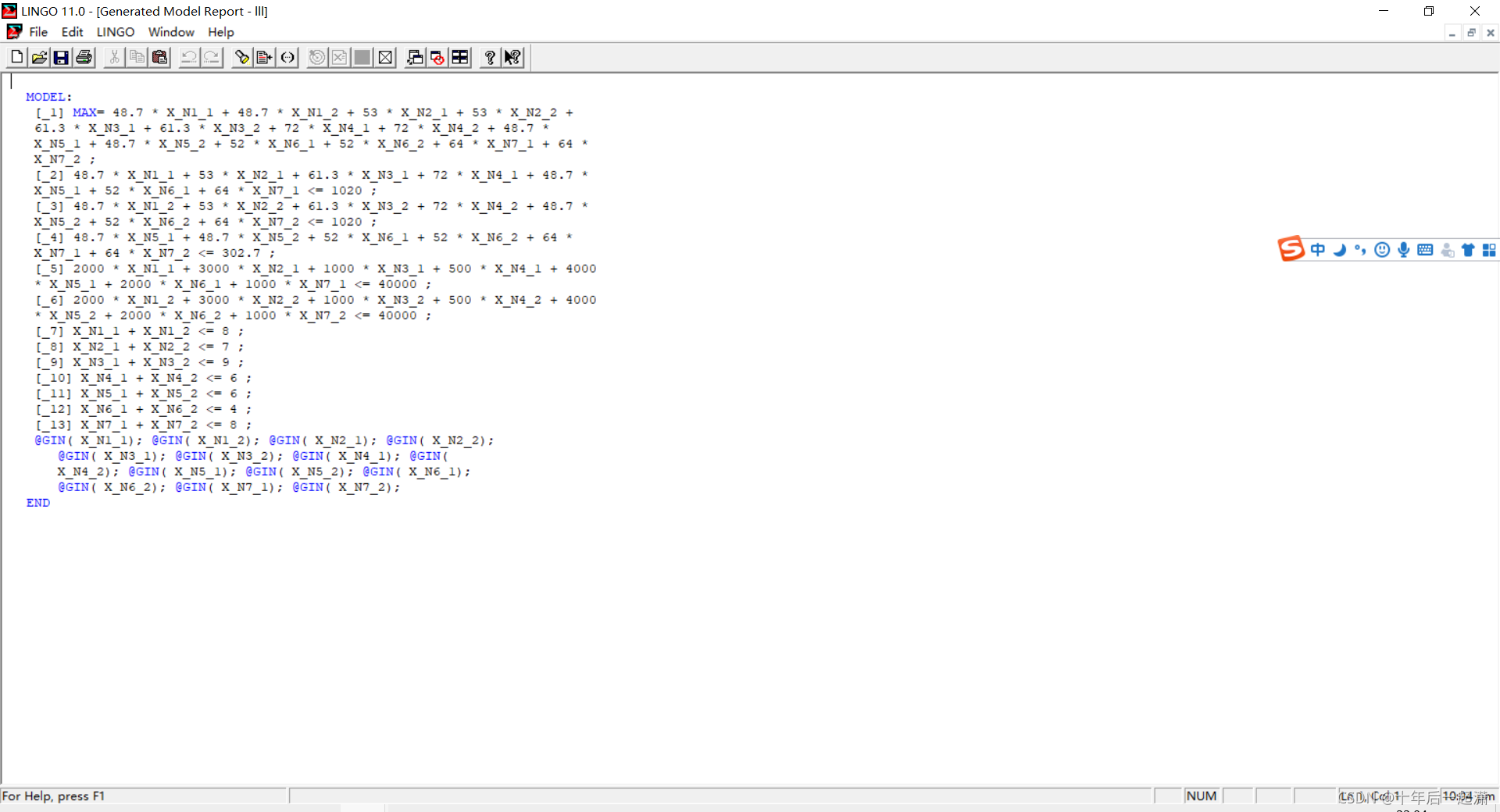







 本文介绍如何使用Lingo优化算法解决实际问题,通过合理安排七种不同规格的包装箱(C1-C7)到两节铁路平板车上,满足载重、长度和空间限制,目标是减少空间浪费。特别关注C5、C6、C7类包装箱的空间总和不超过302.7cm的约束。
本文介绍如何使用Lingo优化算法解决实际问题,通过合理安排七种不同规格的包装箱(C1-C7)到两节铁路平板车上,满足载重、长度和空间限制,目标是减少空间浪费。特别关注C5、C6、C7类包装箱的空间总和不超过302.7cm的约束。

















 1548
1548

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










