机器学习系列17-无监督学习之PCA推导(Ⅰ)

Unsupervised Learning: PCA(Ⅰ)

如果本文对你有帮助，请给我的github打个star叭，上面附有全系列目录和内容！
注：更多优质内容欢迎关注我的微信公众号“Sakura的知识库”：

本文将主要介绍PCA算法的数学推导过程

上一篇文章提到，PCA算法认为降维就是一个简单的linear function，它的input x和output z之间是linear transform，即$z=Wx$，PCA要做的，就是根据$x$把W给找出来($z$未知)

PCA for 1-D

为了简化问题，这里我们假设z是1维的vector，也就是把x投影到一维空间，此时w是一个row vector

$z_1=w^1\cdot x$，其中$w^1$表示$w$的第一个row vector，假设$w^1$的长度为1，即$||w^1|{|}_2=1$，此时$z_1$就是$x$在$w^1$方向上的投影

那我们到底要找什么样的$w^1$呢？

假设我们现在已有的宝可梦样本点分布如下，横坐标代表宝可梦的攻击力，纵坐标代表防御力，我们的任务是把这个二维分布投影到一维空间上

我们希望选这样一个$w^1$，它使得$x$经过投影之后得到的$z_1$分布越大越好，也就是说，经过这个投影后，不同样本点之间的区别，应该仍然是可以被看得出来的，即：

• 我们希望找一个projection的方向，它可以让projection后的variance越大越好

• 我们不希望projection使这些data point通通挤在一起，导致点与点之间的奇异度消失

• 其中，variance的计算公式：$Var(z_1)=\frac{1}{N}\sum _{z_1}(z_1-\overline{z_1}{)}^2,||w^1|{|}_2=1$，$\overline{z_1}$是$z_1$的平均值

下图给出了所有样本点在两个不同的方向上投影之后的variance比较情况

PCA for n-D

当然我们不可能只投影到一维空间，我们还可以投影到更高维的空间

对$z=Wx$来说：

• $z_1=w^1\cdot x$，表示$x$在$w^1$方向上的投影
• $z_2=w^2\cdot x$，表示$x$在$w^2$方向上的投影
• …

$z_1,z_2,...$串起来就得到$z$，而$w^1,w^2,...$分别是$W$的第1,2,…个row，需要注意的是，这里的$w^i$必须相互正交，此时$W$是正交矩阵(orthogonal matrix)，如果不加以约束，则找到的$w^1,w^2,...$实际上是相同的值

Lagrange multiplier

求解PCA，实际上已经有现成的函数可以调用，此外你也可以把PCA描述成neural network，然后用gradient descent的方法来求解，这里主要介绍用拉格朗日乘数法(Lagrange multiplier)求解PCA的数学推导过程

注：$w^i$和$x$均为列向量，下文中类似$w^i\cdot x$表示的是矢量内积，而$(w^i{)}^T\cdot x$表示的是矩阵相乘

calculate $w^1$

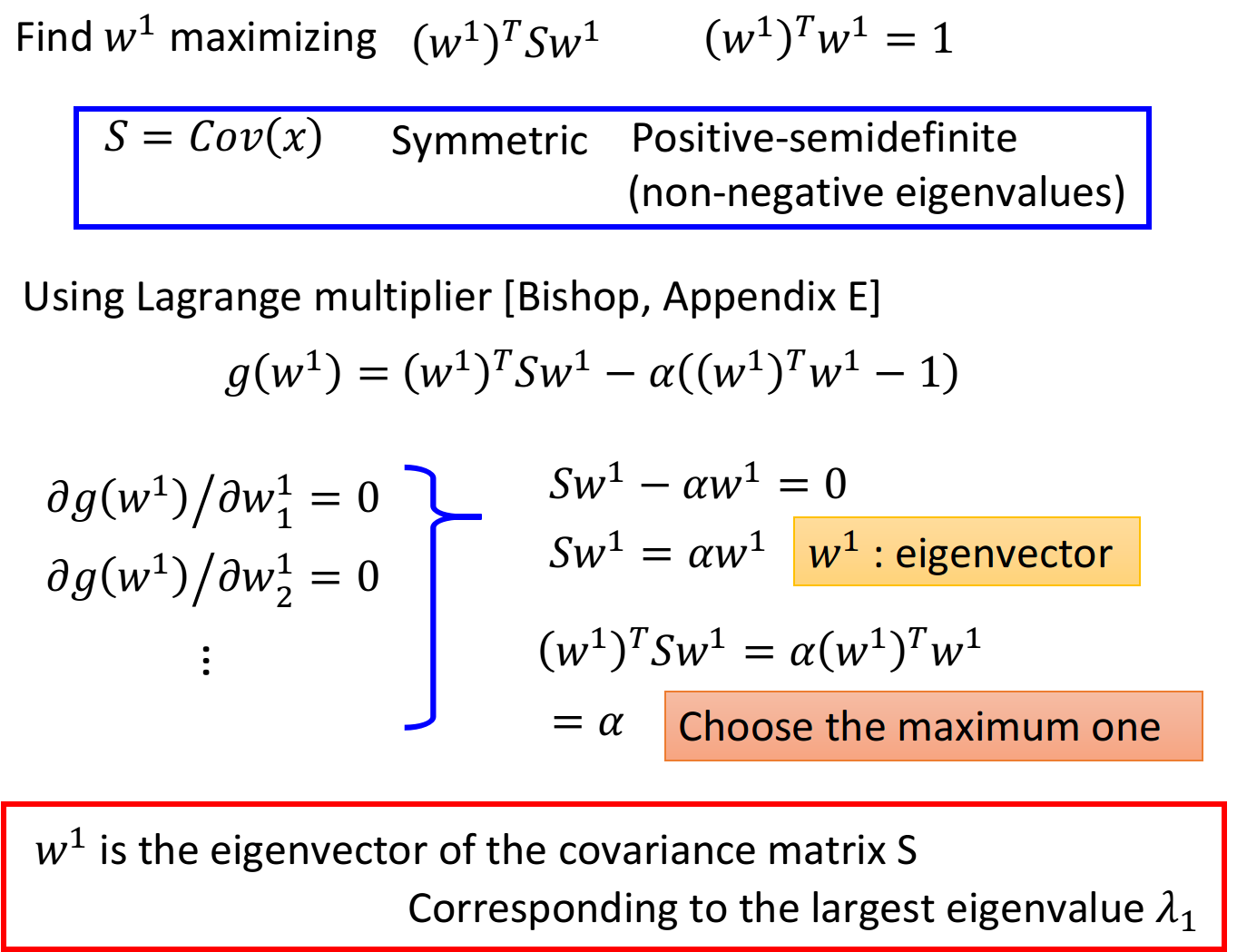
目标：maximize $(w¹⁾TSw^1 $，条件：$(w¹⁾Tw^1=1$

• 首先计算出$\overline{z_1}$：

  KaTeX parse error: No such environment: split at position 10: \begin{̲s̲p̲l̲i̲t̲}̲ &z_1=w^1\cdo…

• 然后计算maximize的对象$Var(z-1)$：

  其中$Cov(x)=\frac{1}{N}\sum (x-\bar{x})(x-\bar{x}{)}^T$

  KaTeX parse error: No such environment: split at position 10: \begin{̲s̲p̲l̲i̲t̲}̲ Var(z_1)&=\f…

• 当然这里想要求$Var(z_1)=(w^1{)}^{T}Cov(x)w^1$的最大值，还要加上$||w^1|{|}_2=(w^1{)}^T{w}^1=1$的约束条件，否则$w^1$可以取无穷大

• 令$S=Cov(x)$，它是：

  • 对称的(symmetric)
  • 半正定的(positive-semidefine)
  • 所有特征值(eigenvalues)非负的(non-negative)

• 使用拉格朗日乘数法，利用目标和约束条件构造函数：

  $$g(w^1)=(w^1{)}^{T}S{w}^1-\alpha ((w^1{)}^T{w}^1-1)$$

• 对$w^1$这个vector里的每一个element做偏微分：

  $$\begin{gathered} \partial g(w^1)/\partial w_1^1=0 \\ \partial g(w^1)/\partial w_2^1=0 \\ \partial g(w^1)/\partial w_3^1=0 \\ ... \end{gathered}$$

• 整理上述推导式，可以得到：

  其中，$w^1$是S的特征向量(eigenvector)

  $$S{w}^1=\alpha w^1$$

• 注意到满足$(w^1{)}^T{w}^1=1$的特征向量$w^1$有很多，我们要找的是可以maximize $(w^1{)}^{T}S{w}^1$的那一个，于是利用上一个式子：

  $$(w^1{)}^{T}S{w}^1=(w^1{)}^T\alpha w^1=\alpha (w^1{)}^T{w}^1=\alpha$$

• 此时maximize $(w^1{)}^{T}S{w}^1$就变成了maximize $\alpha$，也就是当$S$的特征值$\alpha$最大时对应的那个特征向量$w^1$就是我们要找的目标

• 结论：$w^1$是$S=Cov(x)$这个matrix中的特征向量，对应最大的特征值${\lambda }_1$

calculate $w^2$

在推导$w^2$时，相较于$w^1$，多了一个限制条件：$w^2$必须与$w^1$正交(orthogonal)

目标：maximize $(w^2{)}^{T}S{w}^2$，条件：$(w^2{)}^T{w}^2=1,(w^2{)}^T{w}^1=0$

结论：$w^2$也是$S=Cov(x)$这个matrix中的特征向量，对应第二大的特征值${\lambda }_2$

• 同样是用拉格朗日乘数法求解，先写一个关于$w^2$的function，包含要maximize的对象，以及两个约束条件

  $$g(w^2)=(w^2{)}^{T}S{w}^2-\alpha ((w^2{)}^T{w}^2-1)-\beta ((w^2{)}^T{w}^1-0)$$

• 对$w^2$的每个element做偏微分：

  $$\begin{gathered} \partial g(w^2)/\partial w_1^2=0 \\ \partial g(w^2)/\partial w_2^2=0 \\ \partial g(w^2)/\partial w_3^2=0 \\ ... \end{gathered}$$

• 整理后得到：

  $$S{w}^2-\alpha w^2-\beta w^1=0$$

• 上式两侧同乘$(w^1{)}^T$，得到：

  $$(w^1{)}^{T}S{w}^2-\alpha (w^1{)}^T{w}^2-\beta (w^1{)}^T{w}^1=0$$

• 其中$\alpha (w^1{)}^T{w}^2=0,\beta (w^1{)}^T{w}^1=\beta$，

  而由于$(w^1{)}^{T}S{w}^2$是vector×matrix×vector=scalar，因此在外面套一个transpose不会改变其值，因此该部分可以转化为：

  注：S是symmetric的，因此$S^T=S$

  KaTeX parse error: No such environment: split at position 10: \begin{̲s̲p̲l̲i̲t̲}̲ (w^1)^TSw^2&…

  我们已经知道$w^1$满足$S{w}^1={\lambda }_1{w}^1$，代入上式：
  KaTeX parse error: No such environment: split at position 10: \begin{̲s̲p̲l̲i̲t̲}̲ (w^1)^TSw^2&…

• 因此有$(w^1{)}^{T}S{w}^2=0$，$\alpha (w^1{)}^T{w}^2=0$，$\beta (w^1{)}^T{w}^1=\beta$，又根据

  $$(w^1{)}^{T}S{w}^2-\alpha (w^1{)}^T{w}^2-\beta (w^1{)}^T{w}^1=0$$

  可以推得$\beta =0$

• 此时$S{w}^2-\alpha w^2-\beta w^1=0$就转变成了$S{w}^2-\alpha w^2=0$，即

  $$S{w}^2=\alpha w^2$$

• 由于$S$是symmetric的，因此在不与$w_1$冲突的情况下，这里$\alpha$选取第二大的特征值${\lambda }_2$时，可以使$(w^2{)}^{T}S{w}^2$最大

• 结论：$w^2$也是$S=Cov(x)$这个matrix中的特征向量，对应第二大的特征值${\lambda }_2$

PCA-decorrelation

$z=W\cdot x$

神奇之处在于$Cov(z)=D$，即z的covariance是一个diagonal matrix，推导过程如下图所示

PCA可以让不同dimension之间的covariance变为0，即不同new feature之间是没有correlation的，这样做的好处是，减少feature之间的联系从而减少model所需的参数量

如果你把原来的input data通过PCA之后再给其他model使用，那这些model就可以使用简单的形式，而无需考虑不同dimension之间类似$x_1\cdot x_2,x_3\cdot x_5^3,...$这些交叉项，此时model得到简化，参数量大大降低，相同的data量可以得到更好的训练结果，从而可以避免overfitting的发生

本文主要介绍的是PCA的数学推导，如果你理解起来有点困难，那下一篇文章将会从另一个角度解释PCA算法的原理~