面试必会：二叉搜索树（二叉排序树）构建、插入、验证详细图解，奶奶都看懂了，附二叉搜索树的二种验证方法python代码

1、二叉排序树（Binary Sort Tree）性质：

或是一颗空树，或是具有如下性质的二叉树：

(1) 若它的左子树不空，则 左子树 上所有结点的值 均小于 它的根结点的值；

(2) 若它的右子树不空，则 右子树 上所有结点的值 均大于 它的根结点的值；

(3) 它的 左、右子树又分别为二叉排序树 。

重要性质：

1、二叉排序树的中序遍历输出一定是一个单调递增的序列。
2、二叉排序树查找指定数值相当于是一个二分查找。

2、二叉排序树举例：

下图中的这颗二叉树就是一颗典型的二叉排序树：

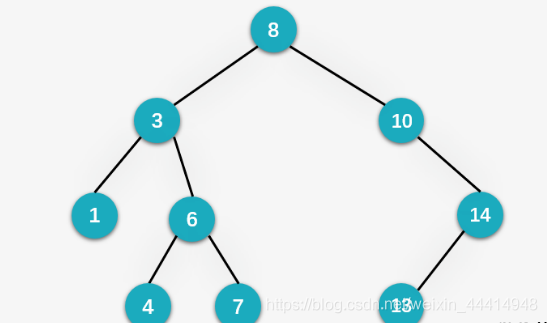
二叉排序树既然是名字当中带有 排序 二字，这就是它相对于普通二叉树的优势所在。

二叉排序树的每个节点上下边界如下图所示，构建、插入均是通过该边界条件判断插入位置：

3、二叉排序树构建、插入规则举例：

假设我们初始时有如下 无序序列：

第一步：插入 8 作为根结点。

第二步：插入 3 ，与根结点 8 进行比较，发现比8小，且根结点没有左孩子，则将 3 插入到 8 的左孩子。

第三步：插入10，首先与根结点比较，发现比 8 大，则要将 10 插入根结点的右子树；根结点 8 的右子树为空，则将 10 作为 8 的右孩子。

第四步：插入 1，首先与根结点比较，比根结点小，则应插入根结点的左子树。再与根结点的左孩子 3 比较，发现比 3 还小，则应插入 3 的左孩子。

第五步：插入 6，先与根结点8比较，小于 8，向左走；再与 3 比较，大于 3，向有走，没有结点，则将6 作为3的右孩子。