SLAM练习题（四）——三维空间刚体旋转_空间旋转的题目怎么写-CSDN博客

本文链接：https://blog.csdn.net/weixin_44456692/article/details/116081863

从零手写SLAM笔记

文章目录

旋转方式转化
讨论
四元数

旋转方式转化

题目1:已知旋转矩阵定义是沿着Z轴旋转45°。请按照该定义初始化旋转向量、旋转矩阵、四元数、欧拉角。请编程实现:

1、以上四种表达方式的相互转换关系并输出,并参考给出的结果验证是否正确。

2、假设平移向量为(1,2,3),请输出旋转矩阵和该平移矩阵构成的欧式变换矩阵,并根据欧式变换矩阵提取旋转向量及平移向量。
**知识点:**1、学习eigen中刚体旋转的四种表达方式,熟悉他们之间的相互转换关系 2、熟悉旋转平移和欧式变换矩阵的相互转换关系

四种旋转方式的初始化：

    // 初始化

    // 旋转向量（轴角）：沿z轴旋转45°
    Eigen::AngleAxisd rotation_vector(M_PI/4, Eigen::Vector3d(0,0,1));
    cout<<"rotation_vector axis=\n"<<rotation_vector.axis()<<endl;
    cout<<"rotation_vector angles\n"<<rotation_vector.angle()<<endl;

    // 旋转矩阵： 沿z轴旋转45°
    Eigen::Matrix3d rotation_matrix = Eigen::Matrix3d::Identity();
    rotation_matrix<<
        0.707, -0.707, 0,
        0.707,  0.707, 0,
        0,      0,     1;
    cout<<"rotation matrix=\n"<<rotation_matrix<<endl;

    // 四元数： 沿z轴旋转45度
    Eigen::Quaterniond quat = Eigen::Quaterniond(0,0,0.383,0.924);  // 赋值方式为（w,x,y,z）
    cout<<"四元数输出方式1：quaternion=\n"<<quat.coeffs()<<endl;    // 输出方式为（x,y,z,w）
    cout<<"四元数输出方式2：\tw="<<quat.w()<<"\tx="<<quat.x()
        <<"\ty="<<quat.y()<<"\tz="<<quat.z()<<endl;
    
    // 欧拉角： 沿z轴旋转45°
    Eigen::Vector3d euler_angles = Eigen::Vector3d(M_PI/4,0,0);// zyx顺序即yaw pitch roll顺序
    cout<<"Euler:yaw pitch roll="<<euler_angles.transpose()<<endl;

旋转矩阵，四元数，旋转向量的相互转化：

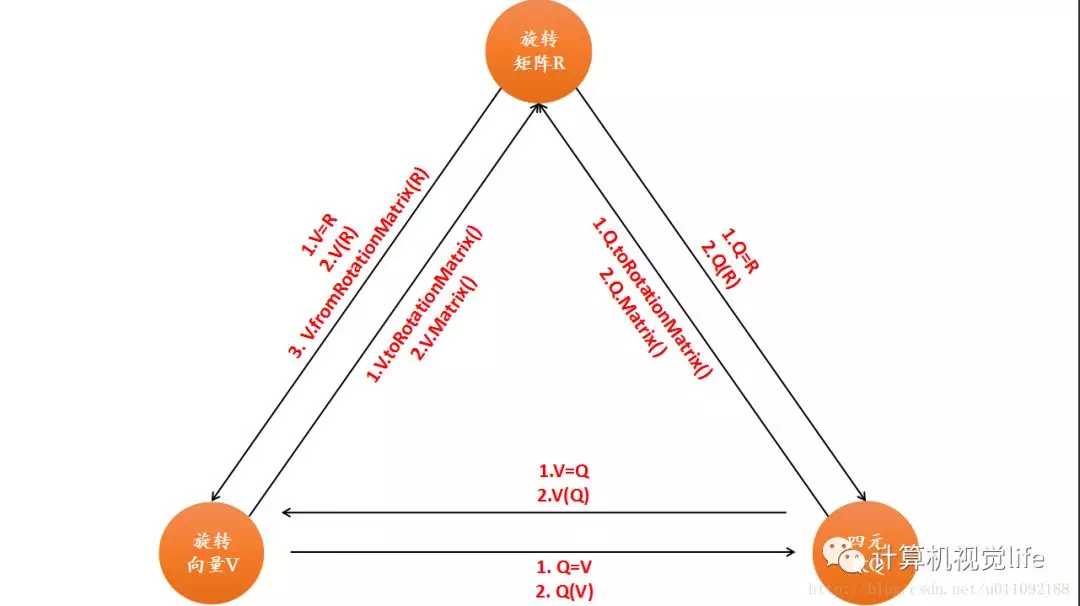
在这里插入图片描述

仔细品一下可以看到，旋转向量和四元数转化为旋转矩阵，Eigen提供了两种函数：toRotationMatrix() 和 Matrix()。

对于旋转矩阵转化为旋转向量，Eigen提供了fromRotationMatrix()。

其余两者转换可以通过eg: V=R or V®两种方式进行赋值。

	// 相互转换关系
    
    // 旋转向量转化为其他形式
    cout<<"旋转向量转化为旋转矩阵方法1：rotation matrix=\n"<<
        rotation_vector.toRotationMatrix()<<endl;
    cout<<"旋转向量转化为旋转矩阵方法2：rotation matrix=\n"<<
        rotation_vector.matrix();
    quat = rotation_vector;
    cout<<"旋转向量转化为四元数：quaternion=\n"<<quat.coeffs()<<endl;

    // 旋转矩阵转换为其他形式
    cout<<"旋转矩阵转换为旋转向量：rotation_vector axis=\n"<<
    rotation_vector.fromRotationMatrix(rotation_matrix).axis()<<
    "\n rotation_vector angle = "<<rotation_vector.fromRotationMatrix(rotation_matrix).angle()<<endl;
    // fromRotationMatrix 参数只适用于旋转向量，不适用于四元数

    rotation_vector = rotation_matrix;
    cout<<"旋转矩阵直接给旋转向量赋值初始化： rotation_vector angle= \n"<<rotation_vector.angle()<<endl;
    cout<<"rotation_vector axis=\n"<<rotation_vector.axis()<<endl;

    euler_angles = rotation_matrix.eulerAngles(2,1,0); //难点 z y x 
    cout<<"旋转矩阵转化为欧拉角： yaw pitch roll="<<euler_angles.transpose()<<endl;
    quat = rotation_matrix;
    cout<<"旋转矩阵转化为四元数：quaternion=\n"<<quat.coeffs()<<endl;

    // 四元数转换为其他形式
    rotation_vector = quat;
    cout<<"四元数转化为旋转向量：rotation_vector axis=\n"<<rotation_vector.axis()
        <<"rotation_vector angle=\n"<<rotation_vector.angle()<<endl;
    
    rotation_matrix = quat.toRotationMatrix();
    cout<<"四元数转换为旋转矩阵方法1：rotation matrix=\n"<<rotation_matrix<<endl;

    rotation_matrix = quat.matrix();
    cout<<"四元数转化为旋转矩阵方法2：rotation matrix=\n"<<rotation_matrix<<endl;

要特别注意旋转矩阵转化为欧拉角：

euler_angles = rotation_matrix.eulerAngles(2,1,0); //难点 z y x

参数2 1 0表示按z y x 也就是按yaw ,pitch,roll的顺序表示欧拉角

欧式变换矩阵：

// 欧式变换矩阵使用Eigen::Isometry ,仿射变换用Eigen::Affine3d, 射影变换用Eigen::Projective3d
    Eigen::Isometry3d T = Eigen::Isometry3d::Identity();    // 初始化
    T.rotate(rotation_vector);
    Eigen::Vector3d v1 = Eigen::Vector3d(1,2,3);
    T.pretranslate(v1);

    cout<<"Transform matrix = \n"<<T.matrix()<<endl;
    cout<<"rotation matrix of T is :\n"<<T.rotation()<<endl;
    cout<<"translation of T is :\n"<<T.translation()<<endl;

注意到初始化T的旋转部分的函数是rotate(),而输出T的旋转部分函数是rotation()。

对于函数命名的感悟：似乎函数赋值这类的函数名字一般用动词，而输出已有的成员的时候用名词。这样做确实更加符合逻辑。

讨论

(参考星球讨论)
问:

在旋转矩阵直接转换成欧拉角代码里rotation_matrix.eulerAngles(2.1.0)这里的2,1,0代表什么意思?

答:分别是代表不同的坐标轴 :代码中注释是rotation_matrix.eulerAngles(2, 1, 0); // ZYX顺序,即roll pitch
yaw顺序。查一下eigen官网,看如下链接Eigen: Geometry module发现了 Each of the three parameters a0,a1,a2
represents the respective rotation axis as an integer in {0,1,2}. For instance, in:Vector3f ea = mat.eulerAngles(2, 0, 2); “2” represents the z axis and “0” the x axis, etc.

欧氏变换矩阵使用代码里T.rotate()这个括号里是不是可以选择另一种方式旋转?

答：是的,具体支持的类型也是要去看定义,在这里Eigen: Eigen::Transform< _Scalar, _Dim, _Mode, _Op…可以看
到支持我们所有的旋转类型。

提示:遇到不懂函数可以去查找定义,要多看多写代码。

附：旋转矩阵的计算方法：

在这里插入图片描述

rot(x, θ）表示绕X轴旋转 θ表示旋转的角度其它同理。矩阵右下角的表示放大倍数，矩阵第4行和第4列可以不要

四元数

题目:单位四元数q可以表达旋转。一个三维空间点可以用虚四元数p表示,用四元数 q 旋转点 p 的结果p’为:
$p'=qpq^{-1}$ ,证明:此时 p′ 必定为虚四元数(实部为零)。
知识点:四元数
参考答案:《视觉SLAM十四讲》P55页留题

设
$q=[s,v_a] , p=[0,v_b ]$
根据四元数的逆
$\mathbf q^{-1}= \frac{q*}{||q||^2} = \frac{1}{||q||^2}[s,-v_a]$
根据四元数乘法
$qp=[-v_a^Tv_b, sv_b+v_a×v_b]$
再计算 $qpq^{-1}$ ,利用四元数乘法公式，得其实部：
$\begin{aligned} & \frac{1}{\|q\|^{2}}\left(-v_{a}^{T} v_{b} s+\left(s v_{b}+v_{a} \times v_{b}\right)^{T} v_{a}\right) \\ =& \frac{1}{\|q\|^{2}}\left(-v_{a}^{T} v_{b} s+s v_{b}^{T} v_{a}+\left(v_{a} \times v_{b}\right)^{T} v_{a}\right) \\ =& 0 \end{aligned}$