数据结构之--非递归后序遍历的两种实现

最新推荐文章于 2024-04-27 16:11:04 发布

逝去的粒子

最新推荐文章于 2024-04-27 16:11:04 发布

阅读量2.3k

点赞数 8

文章标签：算法二叉树数据结构

本文链接：https://blog.csdn.net/weixin_44462351/article/details/105693958

版权

大家好，我是逝去的粒子，今天带来的是非递归后序的两种实现方法，大家选取适合自己的一种即可，提高算法思想是我们的目标。

第一步：了解为什么要学习这个
1.考研数据结构需要会
2.可以提高自己的编程思想，而不是一个码农机器
3.完整代码请大家放心，我统一放在文章最后，不必担心有头没尾！

第一种思想
第一种思想也是我从网上看到的，非常感谢。具体是说：当我们借助栈存放节点，并模拟后续遍历时，会发现每一个节点都会在栈头出现2次，然后才出栈，根据这个规律，我们制定了相应的二次判断结构。

手动步骤演示
假设我们有如下这样一个二叉树,手动演示后序遍历->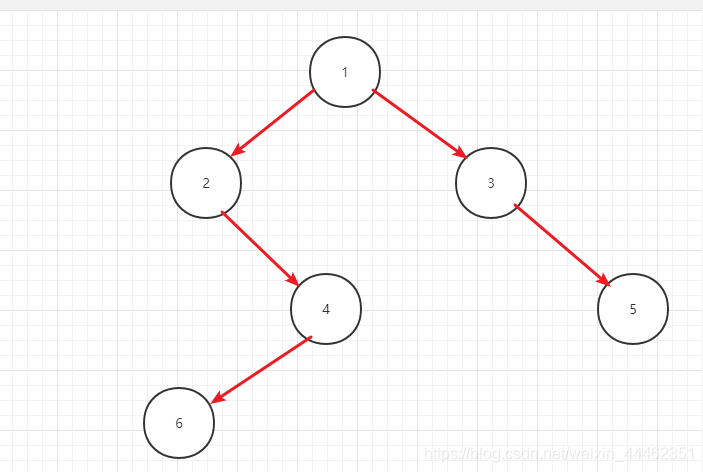 在这里插入图片描述
节点1进栈->第一次出现
节点2进栈->第一次出现
节点2无左子树，出栈，转向右子树，进栈->第二次出现
节点4进栈->第一次出现
节点6进栈->第一次出现
节点6寻找右子树，出栈，转向右子树，进栈->第二次出现
节点6进行出栈，符合第二次出现，出栈，不再对其进栈操作
节点4出栈，符合第二次出现，出栈
节点2出栈，符合第二次出现，出栈
节点1寻找右子树，出栈，转向右子树，进栈，->第二次出现
节点3进栈，->第一次出现
节点3寻找右子树，出栈，转向右子树，进栈，->第二次出现
…以下类推即可

代码实现

//二次判断结构
typedef struct BTNode{
	BiTNode *bnode;
	bool isFirst;
}BTNode;
bnode：是指向一个节点的指针
isFirst：是判断是否二次出现

有了判断结构之后，就可以直接写代码了，如下：

//非递归后序遍历
void PostOrder2(BiTree T){
	SqStack s;
	InitStack(s);
	BiTree p=T;
	BTNode *temp;
	while(p!=NULL||!StackEmpty(s)){
		while(p!=NULL){
			BTNode *btn=(BTNode*)malloc(sizeof(BTNode));
			btn->bnode=p;
			btn->isFirst=true;
			Push(s,btn);
			p=p->lchild;
		}
		if(!StackEmpty(s)){
			temp=Pop(s);	//接收弹出来的节点
			if(temp->isFirst==true){
				temp->isFirst=false;
				Push(s,temp);
				p=temp->bnode->rchild;
			}
			else{
				printf("%c",temp->bnode->data);
				p=NULL;
			}
		}
	}
}
代码实现的一个不同就是，我的p指针只是作为遍历用的，并不进栈，我找了一个能指向当前节点的btn节点，进行进栈出栈操作。

这样的话，我么就借助于栈和一个辅助结构进行了实现操作，只要能看懂手动演示的步骤，那么代码也就能看懂，如果觉得看不懂示意图，请下方留言，我将第一时间进行修改。

极其推荐->第二种思想:
第二种思想是我十分推荐的，简洁明了，后序遍历是：左子树->右子树->根节点，当用栈储存节点，只需分清返回根节点的，是从左子树返回的，还是从右子树返回的，所以，使用辅助指针r，指向最近访问过的节点。

代码有注释，可以边看边手动实现具体过程，加强记忆。

代码实现

void Post(BiTree &T){
	SqStack s;							//初始化栈
	InitStack(s);						
	BiTree p=T,r;						//工作指针p和r
	while(p!=NULL||!StackEmpty(s)){
		if(p){
			Push(s,p);
			p=p->lchild;
		}
		else{
			GetTop(s,p);					//栈的基本方法，在此的作用是返回当前根节点
			if(p->rchild&&p->rchild!=r){	//如果右子树存在，且未被访问过
				p=p->rchild;				//转向右
				Push(s,p);					//进栈
				p=p->lchild;				//再走到最左
			}
			else{
				Pop(s,p);					//弹栈并访问
				printf("%c",p->data);
				r=p;					//记录最近访问的节点
				p=NULL;					//节点访问完后，重置p指针
			}
		}
	}
}

结尾：
可能会有同学会说，你这两个实现根本就是一个思想而已，只是用了不同的工具，确实会很相似，但是我们学习更要看重的是两个之间的小小差别，不是吗，希望会帮助到大家，谢谢。

完整代码–第一种方法

#include "stdio.h"
#include "stdlib.h"
#define MaxSize 50
typedef int ElemType;

//二叉树节点结构
typedef struct BiTNode{
	ElemType data;
	struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

//栈的定义
//typedef struct{
//	BiTree data[MaxSize];
//	int top;
//}SqStack;

//二次判断结构
typedef struct BTNode{
	BiTNode *bnode;
	bool isFirst;
}BTNode;

typedef struct{
	BTNode* data[MaxSize];
	int top;
}SqStack;

//初始化
void InitStack(SqStack &s){
	s.top=-1;
}

//判断栈空
bool StackEmpty(SqStack &s){
	if(s.top==-1)
		return true;
	else
		return false;
}	

//进栈
/*
bool Push(SqStack &s,BiTree x){
	if(s.top==MaxSize-1){
		return false;
	}
	s.data[++s.top]=x;
	return true;
}
*/
bool Push(SqStack &s,BTNode *x){
	if(s.top==MaxSize-1){
		return false;
	}
	s.data[++s.top]=x;
	return true;
}
//出栈
/*
BiTree Pop(SqStack &s){
	BiTree x;
	if(s.top==-1){
		return false;
	}
	x=s.data[s.top--];
	return x;
}
*/
BTNode* Pop(SqStack &s){
	BTNode *x;
	if(s.top==-1){
		return false;
	}
	x=s.data[s.top--];
	return x;
}
//读取栈顶元素
/*
bool GetTop(SqStack &s){
	BiTree x;
	if(s.top==-1){
		return false;
	}
	x=s.data[s.top];
	printf("%c",x->data);
	return true;
}
*/

//默认先序输入递归创建二叉树
void CreateBiTree(BiTree &T){
	char c;
	scanf("%c",&c);
	if(c=='#')
		T=NULL;
	else{
		T=(BiTree)malloc(sizeof(BiTNode));	//创建节点
		T->data=c;
		CreateBiTree(T->lchild);
		CreateBiTree(T->rchild);
	}
}

//先序递归遍历
void PreOrder(BiTree T){
	if(T!=NULL){
		printf("%c",T->data);
		PreOrder(T->lchild);
		PreOrder(T->rchild);
	}
}

//中序递归遍历
void InOrder(BiTree T){
	if(T!=NULL){
		InOrder(T->lchild);
		printf("%c",T->data);
		InOrder(T->rchild);
	}
}

//后序递归遍历
void PostOrder(BiTree T){
	if(T!=NULL){
		PostOrder(T->lchild);
		PostOrder(T->rchild);
		printf("%c",T->data);
	}
}


//非递归后序遍历
/*
void PostOrder2(BiTree T){
	SqStack s;
	InitStack(s);
	BiTree p=T;
	BTNode *temp;
	while(p!=NULL||!StackEmpty(s)){
		while(p!=NULL){
			BTNode *btn=(BTNode*)malloc(sizeof(BTNode));
			btn->bnode=p;
			btn->isFirst=true;
			Push(s,btn);
			p=p->lchild;
		}
		if(!StackEmpty(s)){
			temp=Pop(s);	//接收弹出来的节点
			if(temp->isFirst==true){
				temp->isFirst=false;
				Push(s,temp);
				p=temp->bnode->rchild;
			}
			else{
				printf("%c",temp->bnode->data);
				p=NULL;
			}
		}
	}
}
*/

void PostOrder2(BiTree T){
	SqStack s;
	InitStack(s);	//初始化栈s
	BiTree p=T;
	BTNode *temp;
	while(p!=NULL||!StackEmpty(s)){
		while(p){
			BTNode *btn=(BTNode*)malloc(sizeof(BTNode));
			btn->bnode=p;
			btn->isFirst=true;
			Push(s,btn);
			p=p->lchild;
		}
		if(!StackEmpty(s)){
			temp=Pop(s);
			if(temp->isFirst==true){
				temp->isFirst=false;
				Push(s,temp);
				p=temp->bnode->rchild;
			}
			else{
				printf("%c",temp->bnode->data);
				p=NULL;
			}
		}
	}
}

void main(){
	BiTree T;
	CreateBiTree(T);
	PostOrder(T);
	printf("\n");
	PostOrder2(T);
	printf("\n");
}

完整代码–第二种方法

#include "stdio.h"
#include "stdlib.h"
#define MaxSize 50
typedef int ElemType;

//二叉树节点结构
typedef struct BiTNode{
	ElemType data;
	struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

//队列的结构
typedef struct{
	BiTree data[MaxSize];		//存放队列元素
	int front,rear;				//队头指针，队尾指针
}SqQueue;

//栈的定义
typedef struct{
	BiTree data[MaxSize];
	int top;
}SqStack;

//初始化
void InitStack(SqStack &s){
	s.top=-1;
}

//判断栈空
bool StackEmpty(SqStack &s){
	if(s.top==-1)
		return true;
	else
		return false;
}	

//进栈
bool Push(SqStack &s,BiTree x){
	if(s.top==MaxSize-1){
		return false;
	}
	s.data[++s.top]=x;
	return true;
}
//出栈
bool Pop(SqStack &s,BiTree &x){
	if(s.top==-1){
		return false;
	}
	x=s.data[s.top--];
	return true;
}

//读取栈顶元素
bool GetTop(SqStack &s,BiTree &x){
	if(s.top==-1){
		return false;
	}
	x=s.data[s.top];
//	printf("%c",x->data);
	return true;
}


//默认先序输入递归创建二叉树
void CreateBiTree(BiTree &T){
	char c;
	scanf("%c",&c);
	if(c=='#')
		T=NULL;
	else{
		T=(BiTree)malloc(sizeof(BiTNode));	//创建节点
		T->data=c;
		CreateBiTree(T->lchild);
		CreateBiTree(T->rchild);
	}
}

//先序递归遍历
void PreOrder(BiTree T){
	if(T!=NULL){
		printf("%c",T->data);
		PreOrder(T->lchild);
		PreOrder(T->rchild);
	}
}

//中序递归遍历
void InOrder(BiTree T){
	if(T!=NULL){
		InOrder(T->lchild);
		printf("%c",T->data);
		InOrder(T->rchild);
	}
}

//后序递归遍历
void PostOrder(BiTree T){
	if(T!=NULL){
		PostOrder(T->lchild);
		PostOrder(T->rchild);
		printf("%c",T->data);
	}
}




//第11题:对于元素值为x的节点，删除以它为根的子树----------未解决
void DeleteXTree(BiTree &T){
	if(T){
		DeleteXTree(T->lchild);
		DeleteXTree(T->rchild);
		free(T);
	}
}
void Search(BiTree &T,int x){
	x=x+48;
	BiTree p;
	SqQueue Q;
	InitQueue(Q);
	if(T){
		if(T->data==x){
			DeleteXTree(T);
			exit(0);
		}
	}
	EnQueue(Q,T);
	while(!isEmpty(Q)){
		DeQueue(Q,p);
		if(p->lchild){
			if(p->lchild->data==x){
				DeleteXTree(p->lchild);
				p->lchild=NULL;
			}
			else{
				EnQueue(Q,p->lchild);
			}
		}
		if(p->rchild){
			if(p->rchild->data==x){
				DeleteXTree(p->rchild);
				p->rchild=NULL;
			}
			else{
				EnQueue(Q,p->rchild);
			}
		}
	}
}

void Post(BiTree &T){
	SqStack s;							//初始化栈
	InitStack(s);						
	BiTree p=T,r;						//工作指针p和r
	while(p!=NULL||!StackEmpty(s)){
		if(p){
			Push(s,p);
			p=p->lchild;
		}
		else{
			GetTop(s,p);					//栈的基本方法，在此的作用是返回当前根节点
			if(p->rchild&&p->rchild!=r){	//如果右子树存在，且未被访问过
				p=p->rchild;				//转向右
				Push(s,p);					//进栈
				p=p->lchild;				//再走到最左
			}
			else{
				Pop(s,p);					//弹栈并访问
				printf("%c",p->data);
				r=p;					//记录最近访问的节点
				p=NULL;					//节点访问完后，重置p指针
			}
		}
	}
}

void main(){
	BiTree T;
	CreateBiTree(T);
	PostOrder(T);
	printf("\n");
	Post(T);
	printf("\n");
}

逝去的粒子

关注

8
点赞
踩
25

收藏

觉得还不错? 一键收藏
0
评论
数据结构之--非递归后序遍历的两种实现

大家好，我是失去的粒子，今天带来的是非递归后序的两种实现方法，大家选取适合自己的一种即可，提高算法思想是我们的目标。第一步：了解为什么要学习这个1.考研数据结构需要会2.可以提高自己的编程思想，而不是一个码农机器3.完整代码请大家放心，我统一放在文章最后，不必担心有头没尾！第一种思想第一种思想也是我从网上看到的，非常感谢。具体是说：当我们借助栈存放节点，并模拟后续遍历时，会发现每一个...
复制链接

扫一扫