《视觉SLAM14讲》学习小结——供小白快速入门ch9

后端1-BA

一、概述

根据前面的学习我们知道，前端的功能和目的是根据观测到的图像确定相机的位姿。这种处理方法一般只用到两帧的图片信息，具有速度快但精度有限的特点。在相机位姿确定之后，我们还可以进一步确定目标点在世界坐标系中的三维坐标。随着时间的增加，我们会不断累积同一个路标的值。这就产生了一个问题，哪个值是正确的呢？一种最直觉的想法就是计算这些路标的平均值所为更高精度的估计值。既然有的更高精度值，那就意味着前面哪些时刻前端送过来的值存在误差。这种现象换一句话说就是前面那些时刻前端的位姿估计存在误差，应该根据新确定的更高精度的值反过来重新对以前前端确定的位姿进行修正，这就是后端的功能。从信息处理的角度来看，前端只能获取当前时刻的观测信息，所以辨识得到的位姿精度有限。后端累积了一批观测信息，自然有可能辨识得到更高的位姿精度。

后端在具体实现上有两种思路，第一种是滤波方法，第二种是非线性优化方法。滤波方法是在每次获得前端送过来的新信息，都与上一次的滤波结果融合形成的新估计。这种处理方法存在着一些问题。其一是新信息数据如果异常，系统无法察觉，从而降低滤波精度甚至导致发散。其二是滤波只能对当前的进行优化，对于的历史数据（那些当前帧无法观测到的点信息）无法修正。因此总得说来优化方法要比滤波方法具有更高的辨识精度，本篇主要讲优化方法。优化方法的本质是根据前端送过来各个时刻的相机位姿，空间点三维坐标提炼出最优的和。可以想象，从相机光心到任何一个的连线若根据对应的转换到同一个相机为下，它们应该重合。由于前端所提供的和存在误差，因此这些线往往不重合。优化的目的就是通过调整前端所提供的和，使得这些光线重合，因此优化又称为光束平差法或捆集调整法（BA，Bundle Adjustment）。需要补充说明的是，这些讨论都是针对路标位置固定的情况，本篇的讨论内容也仅限于这种情况。

二、BA与图优化

1.投影模型和BA代价函数

在ch5中我们已经讨论过相机的成像模型，我们这里简单回顾一下。空间点坐标经过外参或转换成相机坐标，接着投影到归一化坐标系中去得到归一化坐标。归一化坐标经过畸变校正后将结果用内参左乘就得到像素坐标，即我们的观测值。如果相机已标定，则内参和畸变模型是确定的，因此上面过程可用如下模型来表示。

                                                   (1)

这个模型表明，观测误差是由于外参或空间点世界坐标不准确引起的。优化的目的就是要通过调整和，使得最小，即

                                                   (2)

我们需要将上面的模型与ch6中的公式（4）对应起来，以便套用前面介绍的优化方法。那里的优化变量就是这里的和，因此

                                         (3)

显然目标函数。优化的重点在于计算雅可比矩阵，因此将进行泰勒级数展开可得。如前所述，我们在对求导的时候需要考虑正交阵约束，因此引入李群和李代数的概念将改写成，进一步记，则的展开式可写为

                                          (4)

由于负号对优化问题的影响容易处理，因此雅可比矩阵可写成分块形式。在不考虑畸变的情况下的表达式分别为ch7下中的式（13）和（15）。畸变修正的目的是将相机模型修正成无畸变的情况，因此在相机模型有畸变但标定后，的表达式仍然是这两个。根据ch6中的分析，无论是高斯牛顿法还是列文伯格-马夸尔特法，都要计算增量方程中的矩阵

                                          (5)

求解增量方程时需要对求逆。由于空间点的数量很多，因此这种矩阵求逆的计算量非常大。21世纪视觉SLAM的最重要进展之一就是发现矩阵的结构特点并可通过图优化的方法来表示。的结构特点是下一节要讨论的内容

2.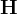矩阵的稀疏性和边缘化

H矩阵稀疏化和边缘化有着丰富的内容，然而本系列博文的目的是为了让读者快速入门视觉SLAM，因此这里略去了许多具有重要学术意义的内容，偏重于具有工程意义的结论。

图1是一个具有2个相机位和6个路标点的场景，连线表示相机位可以观测到路标。我们针对这个场景来分析式（1）中的误差函数。显然，对于每一个组合都会有一个误差函数，因此总共有共8个误差函数。其中的第一个下标表示相机位序号，第二个下标表示路标序号。这种误差函数实际上表示归一化坐标系上的重投影误差，因此是一个二维的列矩阵。将所有的误差函数排成列阵即可得到总误差函数列阵，即，其中分号表示按列排序的意思。将所有的相机位和路标按如下方式排列即可构成优化参数列阵，即。雅可比矩阵就是将对求导数的结果，它将是一个的分块矩阵。其中第一个8表示矩阵中按方块矩阵来算的元素个数，第二个8表示矩阵中按方块来算的元素个数。雅可比矩阵的第i,j个分块元素。显然也是一个矩阵，其元素取决于和的个数。根据前面的分析，的个数都是2。若表示相机位，则其维数为6（相机的位姿需要用中六个元素来描述）。若表示路标，则其维数为3（三维空间位置用三个坐标来表示）。

图1：2相机位6路标的场景相机-路标观测示意图

以为例来看其具体形式

                         (6)

我们发现中仅含有第一个下标所表征相机位的项和第二个下标所表征路标的项，其他所对应的项都为零。根据这个规律，可以绘制出整个的特性示意图，如图2所示

图2：雅可比矩阵的稀疏性和H矩阵的特性

图2中黑色方块表示数据非零，其他的地方数据均为零。与相机位有关的方块比较长是因为表征相机位姿所需要的变量比路标多的缘故。根据这种雅可比矩阵的特性，我们可以求得计算增量方程中矩阵的特性如图2右边所示。矩阵可分解位四个方块矩阵，其左上角矩阵和右下角矩阵均为对角方块矩阵。其左下角方块矩阵和右上角方块矩阵互为转置。

这种特性对于计算ch6中的增量方程非常有帮助。根据的特性可将此增量方程改写为

                                                 (7)

将上述方程两边同时乘以矩阵并整理可得

                                         (8)

这个方程组中，第一行所对应方程的解为。由于矩阵是对角阵，因此求逆不存在困难；矩阵的维数等于相机位的数量，一般比较小，因此的求解不存在困难。在获得后将其代入第二行所对应的方程可求得。如前所述，是对角阵，因此的计算也不存在困难。

总而言之，通过分析矩阵和的特性，减小了增量方程求解过程中的计算量问题。特别是对于路标点数量比较大的场景，这种处理非常有效。

三、鲁棒核函数

在BA过程中，如果因为某种原因导致观测数据异常，就会使得其所对应的误差函数很大。这种异常的将通过BA过程传递给，使得辨识得到的相机位姿或路标误差很大。解决这个问题的一个有效办法是引入鲁棒核函数，这里介绍其中比较著名的Huber核：

                                              (9)

这个函数表示，当中元素比较小的时候，随的变化是二次函数；当比较大的时候，随的变化是一次函数，如图3所示

图3：Huber核函数与二次函数的对比

将此核函数作用在目标函数中各元素上以得到新的目标函数。可以发现，采用新的目标函数后，如果因数据异常而使得中某元素异常增大时，因为Huber核函数的特性，新目标函数只会合理增大，从而减小这种异常所产生的辨识结果即的误差。

四、小结

本篇讨论后端的BA过程。由于这方面的内容在ch7中也有涉及，因此理解起来也不会困难。和前面章节不同的是，这里着重讨论通过分析雅可比矩阵的稀疏性和增量方程矩阵的结构特性来简化增量方程的求解。这种分析在路标数量比较大的时候非常有效。博文最后介绍了鲁棒核函数Huber及其对BA的作用。