有向无环图与关键路径

一、有向无环图

  即DAG(Directed Acycline Graph)，为图中无环的有向图。
 

1.判断

①深度优先搜索：
 可以使用DFS，找出是否存在环：从某个顶点$v_0$出发，进行DFS，若存在一条从顶点到已访问顶点$v$的回边（即遍历到同一个点两次），则有向图中存在环。

②拓补排序
 
 

2.应用

①表达式共享

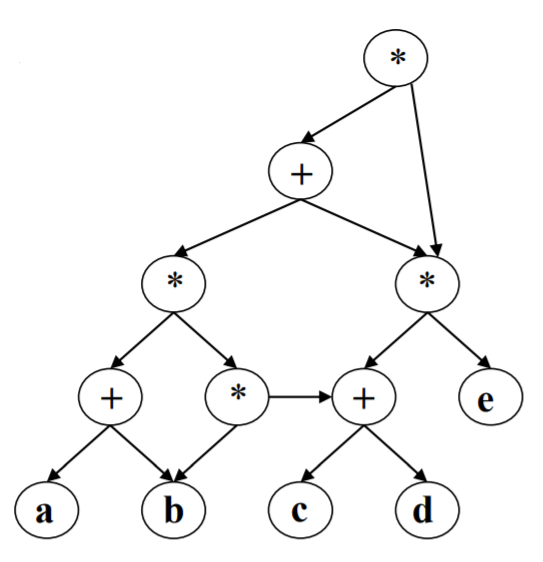
  可用于表示表达式的共享，相比于二叉树的表示形式更节省空间：

二叉树形式：
     
 
有向无环图形式：
         

 

②AOV网

  AOV(Activity On Vertex Network)网，对工程活动加以抽象，图中顶点表示活动，有向边表示活动之间优先关系，这样的有向图称AOV网。AOV网中不能有环，否则，某项活动能否进行是以自生是否完成作为前提条件的。
  可对AOV网进行拓补排序，以求得各子活动之间的优先关系。

 

二、拓补排序

• 拓补有序序列：设$G=V,E$是为n阶有向图，$V$中的顶点序列$v_1,v_2,...,v_n$，满足：若从顶点$v_0$到$v_j$有这样一条路径：顶点序列中$v_0$必在$v_j$之前，这样的顶点序列称为一个拓补有序序列。

• 拓补排序：拓补排序为对一个有向图构造拓补有序序列的过程；构造会有两个结果：

  1. 若全部顶点都被输出，则说明DAG不存在环（回路）。
  2. 若有的顶点没有被输出，则DAG存在环（回路）。

 

1.拓补排序算法

1. 在有向图中选一个没有前驱的顶点作为始点
2. 从图中删除该点与所有以它为尾的弧（改弧的弧头顶点入度减1）
3. 重复①②，直到图中不再有没有前驱（入度为0）的顶点为止

如何选择入度为0的顶点：
 使用栈或队列保存入度为0的顶点，新增InDegree记录各顶点的入度。

 
 

2.数据结构的实现

1. 邻接表：
    由于拓补排序过程中需要始终查找入度为0的顶点，故需为每个顶点结构新增一个入度域InDegree；且每遍历一个顶点需要对以其为尾的弧进行遍历，找到所有邻接点，再将他们的入度域减一。其间涉及大量链表遍历，显然使用邻接矩阵更为方便。

实现：

//数据结构
#define MAXVERTEXNUM 100

struct ArcNode{
	int AdjVex;
	ArcNode *NextArc;
};

struct VexNode{
	int InDegree;
	char Data;
	ArcNode *firstArc;
};

class Graph{
	int VertexNum;
	VexNode *AdjList;
}

//具体算法
void TopologicalSort(){
	stack<VexNode> S; 	//存放入度为零的顶点
	VexNode v;
	ArcNode* w;
	int i,count;
	for(int i=0;i<VertexNum;i++)
		if(!AdjList[i].InDegree)	S.push(AdjList[i]);	//入度为零的顶点入栈
	count=0;		//计数器置0
	while(!S.empty()){
		v=S.top();
		S.pop();
		count++;
		cout<<v.Data<<" ";
		for(w=v.fristArc;w;w=w->NextArc){
			AdjList[w->AdjVex].InDegree--;
			if(!AdjList[w->AdjVex].InDegree)
				S.push(AdjList[w->AdjVex];)
		}
	}
	if(cout<VertexNum)	cout<<"图中含有回路";
	cout<<endl;
}

 
2. 邻接矩阵：
  ①逐列扫描矩阵，找到入度为0的顶点$v$
  ②输出顶点$v$，标识$v$已访问
  ③将矩阵第$v$行全部清0（删除所有以该顶点为尾的弧，且剪掉对应弧头顶点的度数）
  ④重复上述不走，直到没有入度为0的顶点

以上方法矩阵最终所有的元素不一定全为0。

 
 

三、关键路径

  对于工程活动，人们不仅关心工程能否顺利完成(对AOV网进行拓补排序)，还关心：

• 估算整个工程完成所需最短时间。
• 影响工程的关键活动是什么，那些活动的延期将会影响整个工程的进度，加速这些活动是否会提高整个工程的效率。

1.参数介绍

 
1.AOE网(Activity On Edge NetWork)：以顶点表示事件(Event)，以有向边表示活动，边上的权值为该活动持续的事件，这样的有向图称为AOE网。利用AOE网可完成以上工作。

• 只有某顶点事件发生后，从该顶点出发的各有向边活动才能开始
• 只有进入某顶点的所有边的各顶点所代表的活动都已结束，该顶点事件才能发生。
• 在AOE网中，时间不能自己完成，而是由活动驱动，随活动的完成而完成。

 
2.关键路径：

• 把AOE网中某路径上各个活动所持续时间之和称为路径长度。
• 从源点到汇点的最大程度的路径称为关键路径，其长度为工程完成的最短时间。关键路径可能不唯一。
• 关键路径上的活动称为关键活动，关键活动是影响整个工程时间的关键所在。
• 顶点：工程需要完成的第一个事件
• 汇点：工程需要完成的最后一个事件

介绍关键路径算法之前，先介绍几个重要参数：

• $V_e(j)$：表示事件$j$的最早发生事件，即从源点到顶点$j$的最长路径长度（只有将所有所需的事件都完成了$j$才能进行）；
• $V_l(k)$：表示事件$k$的最晚发生时间，即从汇点到顶点$k$的最短路径长度（此时事件$k$再不发生则会影响工程的进度）；
• $e(a_i)$：表示活动$a_i$的最早开始时间；
• $i(a_i)$：在不影响进度的前提下，活动$a_i$的最晚开始时间；
• $dut(<j,k>)$：弧$<j,k>$所对应活动的持续时间；

其中$i(a_i)-e(a_i)$表示活动$a_i$的时间余量，即可以推迟多久执行而不影响工程的进度；若$(a_i)-e(a_i)=0$，则表示活动$a_i$为关键活动，即该活动在关键路径上；于是求关键路径的问题就转换成了求各活动的$e(a_i)$与$l(a_i)$，求出所有关键活动后可得关键路径。

 
各参数间的关系：

• $e(a_i)=V_e(j)$，即活动$a_i$的弧尾时间$j$的最早发生时间，当事件$j$发生了，活动$a_i$最早可以现在开始；
• $l(a_i)=V_l(k)-dut(<j,k>)$，即活动$a_i$的弧头事件$k$的最晚发生时间减去活动$a_i$的持续时间——此时活动$a_i$再不发生，则会导致事件$k$推迟，从而事件$k$发生时间晚于最晚时间，导致工程延期。

于是关键路径的求解又转换为求各顶点最早、最晚发生时间。

 
 
各参数的值

1.事件最早开始时间
V e ( j ) = { 0 ， 若 j 为 源 点 M a x { V e ( x ) + d u t ( < x , j > ∣ < x . j > 为 图 中 的 弧 ) } V_e(j)=\begin{cases} 0，若j为源点\\ Max\{V_e(x)+dut(<x,j>|<x.j>为图中的弧)\}\\ \end{cases} Ve​(j)={0，若j为源点Max{Ve​(x)+dut(<x,j>∣<x.j>为图中的弧)}​
 除源点外，只有进入顶点$j$的所有弧所代表的活动全部结束后，事件$j$才能发生。即只有$j$的所有前驱事件$x$的最早发生时间$V_e(x)$计算出来后，才能计算$V_e(j)$。

 
 
2.事件最晚开始时间
V l ( k ) = { V e ( n − 1 ) ， 若 k 是 汇 点 M i n { V l ( y ) − d u t ( < k , y > ∣ < k , y > 为 图 中 的 弧 ) } V_l(k)=\begin{cases} V_e(n-1)，若k是汇点\\ Min\{V_l(y)-dut(<k,y>|<k,y>为图中的弧)\} \end{cases} Vl​(k)={Ve​(n−1)，若k是汇点Min{Vl​(y)−dut(<k,y>∣<k,y>为图中的弧)}​
 只有$k$的所有后继事件$y$的最晚发生时间$V_l(y)$计算出来后，才能计算$V_l(k)$，此时事件$k$再不发生，则会延误后续的事件。

 

2.具体算法

1. 利用拓补排序求出AOE网的一个拓补序列
2. 从拓补序列的源点开始，令$V_e[0]=0$，按拓补顺序依次计算每个事件的最早发生时间$V_e(j)$；
3. 从拓补序列的汇点开始，令$V_l[n]=V_e[n-1]$（终点一定在关键路径上），按逆拓补顺序依次计算每个事件的最晚发生时间$V_l(j)$；
4. 计算每个活动$a_i$的最早开始时间$e(a_i)$和最晚开始时间$l(a_i)$，若$e(a_i)=l(a_i)$，则该活动$a_i$为关键活动，该弧所依附的顶点序列为关键路径，关键路径上的权值之和为完成工程所需的最短时间。

• 只有缩短关键活动时间才能缩短整个工程工期
• 一个项目可以有多个、并行的关键路径。若一个关键活动不在所有的关键路径上，减少它并不能减少工期。