《算法图解》笔记与总结

 写在开头

这是一篇读书笔记式的文章，力求简要地概括《算法图解》 中陌生和重要的内容，所以有的具体内容仍需要参考原书。

值得记录的代码附在文末，使用python编写。

持续更新。

这本书已经读完，这篇笔记也更新至此。不得不说，《算法图解》是一本对新手非常友好的书，内容详细而不啰嗦，十分有条理，只要沿着顺序读下去，基本能够很快理解消化。我很庆幸我是在这本书中第一次接触到诸如动态规划之类的知识点，否则很有可能又被劝退了。当然，由于其篇幅限制，很多常用内容没有介绍到，还需要继续补充，这些内容记录在我的另一篇笔记里。

---

第1章 算法简介

二分查找

大O表示法：O(n)，n指操作数

• 该表示法中的log默认以2为底
• 指出了算法运行时间的增速
• 画16个格子的例子：一个一个画，O(n)；四次对折，O(logn)
• 指出的是最糟情况下的操作数

常见的大O运行时间

• O(log n)
• O(n)
• O(n*log n)
• O(n^2)
• O(n!)，如旅行商问题

随着输入的增加，上述五种算法的操作数的增加由慢到快

---

第2章 选择排序

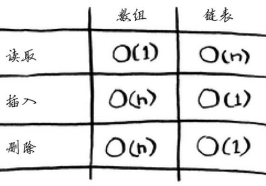
数组与链表的区别：“挨着坐”和“分开坐”

数组在内存中是连续存放的；链表中的元素可以存储在内存的任何地方，链表的每个元素都存储了下一个元素的地址。

数组vs链表

• 当数组增加元素而相邻内存单元已被占用，就需要移动整个数组，链表不存在这个问题
• 需要读取链表最后一个元素时，需要从第一个开始依次读取。当需要同时读取所有元素时，链表效率高，需要跳跃时效率低；数组相反
• 数组支持随机访问，链表只能顺序访问

一个疑惑和其解答

Q：在向链表的中间插入元素时，不需要先从第一个元素逐个获取索引，直到要插入的位置？

A：获取索引即读的过程，不应算在操作数中；只考虑插入这个操作。

数组与列表可以组合使用

facebook存储用户信息的例子

TODO：选择排序的例子，为什么是使用平均每次检查的操作数的平均值来计算O，而不是直观理解的阶乘？

---

第3章 递归

性能

递归并不会比循环提高性能，但可能更容易理解

组成

• 基线条件：控制何时停止调用自己，避免无限循环
• 递归条件：循环调用自己

栈

只对最上层元素执行两种操作：插入、删除并读取（弹出）

调用栈

例子的文字总结：一个函数A中调用了另一个函数B，当A开始执行，内存分配给其一部分，存储其涉及到的所有变量；当执行到B，内存分配给B一部分，并在栈中压在A的部分之上；执行B，其被从栈上弹出，此时A位于最上方，故继续执行A。这个用于储存多个函数的变量的栈，被称为调用栈。

调用另一个函数时，当前函数暂停并处于未完成状态。

递归调用栈：以阶乘为例

要注意，一个变量在每次调用中的值可能不同，在一个调用中不能访问另一个调用中的变量（还是比较符合常识的）

栈的弊端

每次函数调用会占用内存，栈过高占用的内存也过多

解决办法：改用循环；使用尾递归（本书不涉及）

---

第4章 快速排序

分而治之，Divide and Conquer,D&C

• 找出尽可能简单的基线条件
• 不断将问题分解直到满足基线条件

Tip：涉及到数组的递归函数常见的基线条件是数组为空或只含一个元素。

快速排序思路

• 最简单的排序：不需要排序，即数组中只有0或1个元素
• 两个元素的数组，比较二者的值
• 多于两个元素的数组，分而治之
  • 选取一个元素作为基准值（暂取第一个）
  • 分区：遍历，找出比基准值大的和小的元素，分别构成两个数组。目前有：比基准值小的子数组、基准值、比基准值大的子数组
  • 对子数组递归，直到剩下的数组长度小于等于二
  • 子数组排序后，合并

        使用python实现的快排，见代码1

再谈大O表示法 - 比较合并排序和快速排序 - 大O表示法中的常量

例子，逐个打印数组元素的函数，一个没有sleep(1)（记一次sleep的时间为c），另一个有，则其运行时间分别为c*n和n。但是在大O表示法中，固定时间量，也即常数c，是忽略不计的，因为一般来说对时间影响更大的是n和logn的区别。

对于运行时间都为nlogn的快速查找和合并查找，常量的影响就可能很大；快速查找更快，因为其遇上最糟情况的可能性比平均情况低得多。

平均情况和最糟情况

以快速排序的基准值为例，当基准始终选择在开头时（最糟情况），调用栈会非常长，O(n)；而当基准选择在中间（最佳情况），调用栈就短得多，O(log n)。

取一个元素为基准值，并划分数组的操作，不论基准值取在了哪里，划分了多少组，都涉及到了n（数组长度）个元素，即每次调用栈的操作时间都为O(n)。

最佳情况的层数O(log n)，每层操作时间O(n)，所以总时间O(nlog n)；最糟情况层数O(n)，所以总时间O(n^2)。

只要每次的基准值都是随机选择，快速排序的平均运行时间就是O(nlog n)；也就是说，最佳情况也是平均情况 - 这里不求甚解了:(

---

第5章 散列（Hash）表

散列函数

将输入映射到数字

• 必须：一致性：对同样的输入，映射的数字必须相同
• 理想但不必须：对于不同的输入，映射到不同的数字

Maggie的例子

创建一个用于存储物价的空列表

苹果->散列函数->输出一个数字->列表中这个数字的位置存储着苹果的价格

该例子中散列函数的性质：

• 输入相同，输出就相同
• 输入不同，输出就不同
• 只返回有效的输出，如列表长度为5，就不会返回索引为100

散列表：散列函数+数组

一种包含额外逻辑的数据结构，由键和值组成。

数组和链表都被直接映射到内存，但散列表使用散列函数来确定元素的存储位置。

散列表获取元素的速度和数组一样快。

Python的字典就是散列表。

散列表的应用

• 查找，eg：电话薄
• 避免重复，eg：投票
• 缓存，eg：Facebook，当URL在散列表中时，发送缓存中的数据，否则让服务器处理。如此加快了加载速度，并减轻了服务器负担

冲突 

存储apple和avocardo的价格的例子：能够总是将不同的键映射到不同值的散列函数难以实现。

不同的键被分配给了同一个值，即冲突。

最简单的解决办法，在该位置创建链表，依次存储，但是性能不佳。

理想的情况是，散列函数将键均匀映射到散列表的不同位置。一个好的散列函数很重要。

常量时间O(1)

散列表在平均情况下的操作时间为O(1)，不意味着马上，而是不论散列表多大，所需时间都相同。

散列表的性能

平均情况下，散列表的查找（获取给定索引处的值）速度与数组一样快，而插入和删除速度与链表一样快，兼具两者的优点。但在最糟情况，即有冲突的情况下，散列表的各种操作的速度都很慢。

选读：散列表的实现 避开最糟情况

避免冲突的方式

• 较低的填装因子：元素数/位置总数，越低越不容易冲突
• 良好的散列函数：让数组中的值均匀分布

---

第6章 广度优先搜索 图 树

广度优先搜索：寻找解决问题的最短路径的问题，用于图的查找算法

图

图由节点和边组成。一个节点可能与众多节点直接相连，称为邻居。

两类问题

• 从节点A出发，有前往节点B的路径吗？eg：朋友中有无芒果销售商
• 从节点A出发，前往节点B的哪条路径最短？eg：朋友中哪个芒果销售商关系最近

 在名单中依次检查，如果当前人（一度关系）不是销售商，就把他的朋友加入到相应的关系部分（二度关系）（队列的末尾）。实现“依次”，需要数据结构：队列。如果不是依次的，找到的就可能不是最短路径。

队列

队列，先进先出，First In First Out，FIFO

栈，后进先出，Last In First Out，LIFO

在python中

• 创建双端队列：q = deque()
• 向队列添加元素：q += item（可以是数组以一次添加多个）
• 弹出第一个元素：item = q.popleft()

使用散列表实现图

找销售商的例子，创建一个字典，以graph["you"] = ["alice", "bob", "claire"]、graph["alice"] = ["peggy"]的形式添加，即以一人为键，其下级关系的所有人的数组为值。由于散列表是无序的，所以添加内容的顺序也没有影响。

有向图：关系是单向的，eg：有从别人指向Anuj的箭头，但没有从Anuj指向别人的箭头，所以Anuj没有邻居

无向图：没有箭头，直接相连的节点互为邻居

在销售商例子中，由于一个人可能同时是多个人的朋友，为了避免重复检查或无限循环，在检查完一个人后，应将其标记为已检查，且不再检查他。

运行时间

在整个人际关系网中搜索芒果销售商，意味着将沿每条边前行，因此运行时间至少为O（边数）；

使用了一个队列，将一个人添加到队列需要的时间是固定的，O(1)，因此总时间为O(人数)；

所以，广度优先搜索的运行时间为O(V+E)，其中V为顶点数，E为边数。

树

一种特殊的图，其中没有往后指的边。

如果任务A依赖于任务B，在列表中任务A就必须在任务B后面。这被称为拓扑排序，使用它可根据图创建一个有序列表。

合理的顺序：

• 起床 - 刷牙 - 吃早餐 - 洗澡
• 起床 - 刷牙 - 洗澡 - 吃早餐（即吃早餐必须在刷牙后，但不一定紧挨着）

---

第7章 狄克斯特拉算法

加权图：带权重的图。否则是非加权图。

例子：由起点到终点，每一段都有相应的时间（权重）。广度优先搜索找出的是段数最少的路径，狄克斯特拉可用于找出最快（总权重最小）的路径。换言之，广度优先搜索找出的是非加权图的最短路径，狄克斯特拉找出的是加权图的最短路径。

适用范围：没有负权边的有向无环图

步骤

1. 初始化：所有节点的开销（从起点到改节点的最小权重）为无穷大，节点的父节点未知
2. 起点的邻居中，找出开销小的节点A，并将A的父节点设为起点
3. 更新A的所有邻居的开销，如果某邻居C的开销被更新，就说明沿着经过A的路径是开销最小的，所以将C的父节点更新为A
4. 将A标记为已分析
5. 重复２、３、４，继续分析除A以外开销最小的节点，更新其所有邻居的开销和父节点，直到除了终点外的所有节点都被分析
6. 根据父节点可倒推得开销最短的路径

环

从某节点走一圈后又回到该节点。绕环的路径不可能是最短路径。

无向图意味着两个节点彼此指向对方，其实就是环，在无向图中，每条边都是一个环。

狄克斯特拉算法只适用于有向无环图。

负权边

即权重为负的边。

狄克斯特拉算法假设：对于处理过的海报节点，没有前往该节点的更短路径。 这种假设仅在没有负权边时才成立。在琴谱换钢琴的例子中，已经更新过经由海报的路径，但如果有负权边，就相当于找到了前往海报的更短路径，而在狄克斯特拉算法中，经由海报的路径已经更新并不再改变，所以无法正常更新。

不能将狄克斯特拉算法用于包含负权边的图。可以用贝尔曼-福德算法（略）。

代码实现

需要三个散列表和一个数组，用于：

• graph：记录邻居关系和权重（两层）
• costs：更新开销（从起点到该节点的总权重）
• parents：更新父节点
• processed = []：记录已经处理的节点

代码实现见代码2

---

第8章 贪婪算法

有些情况下，完美是优秀的敌人

排课问题与背包问题

一间教室，课的时间有冲突，选出尽可能多且时间不冲突的课程。

• 选出结束最早的课作为要在这间教室上的第一堂课
• 选择第一堂课结束后才开始的课。同样选择结束最早的课作为第二堂课，如此重复

每步都选择局部最优解，最终得到的就是全局最优解

但同样的思路不适用于另一个例子，背包问题：容量35的背包，要装下价值最大的东西，可以装的有重量30价值3000的音响、重量20价值2000的笔记本、重量15价值1500的吉他。如果按照上面的思路，先装入最值钱的音响，就无法再装入别的东西，价值比笔记本+吉他少。

集合覆盖问题

例子：需要让节目被全美50个州的听众都收听得到，在每个广播台播出都需要支付费用，因此力图在尽可能少的广播台播出。每个广播台都覆盖特定的区域，不同广播台的覆盖区域可能重叠。即需要找出覆盖全美50个州的最小广播台集合。

穷举法列出所有可能的集合，子集有2**n个。

需要使用近似算法：

• 选出覆盖了最多的未覆盖州的一个广播台（不考虑它覆盖了多少已覆盖的）
• 重复直到覆盖所有州

该例子的python代码，见代码3

NP完全问题

简单定义是，以难解著称的问题，如旅行商问题和集合覆盖问题。有观点认为不可能编写出可快速解决NP完全问题的算法。

如果能判断出一个问题是不是NP完全问题，就可以决定是否采用贪心算法。不存在判断标准，但可以根据问题的特征判断：

• 元素较少时算法的运行速度非常快，但随着元素数量的增加，速度会变得非常慢
• 涉及“所有组合”的问题
• 不能将问题分成小问题，必须考虑各种可能的情况
• 涉及序列（如旅行商问题中的城市序列）且难以解决
• 涉及集合（如广播台集合）且难以解决
• 可转换为集合覆盖问题或旅行商问题，那它肯定是NP完全问题

---

第9章 动态规划

目的：将某个指标最大化。

背包问题，穷举太复杂，贪心算法可能找出的不是最优解。需要使用动态规划。

动态规划先解决子问题，再逐步解决大问题。

以背包问题为例介绍动态规划

背包容量4磅，音响3000美元4磅，笔记本电脑2000美元3磅，吉他1500美元1磅。

每个动态规划算法都从一个网格开始。表格列标题为容量（不同容量的子背包），行为可选择的商品，每个格子用于记录当前能够装下的最高价值和其对应的组合。每一行的格子考虑当前行所代表的商品和当前行以上的商品，如：第一行，就只能装吉他；第二行只能装音响和吉他，不能考虑笔记本电脑。

 目的是让背包中商品的价值最大，计算每一行时，该行都表示的是当前的最大价值。

更新到第一行时，最大价值是吉他1500美元。

 更新完第一行后的最大价值

 更新完第二行后的最大价值

标题 更新完第二行后的最大价值

 在最后一个单元格，如果偷单价最高的音响，则3000美元；但如果选择笔记本电脑（当前行所读应的），则2000美元，剩下的1磅空间再偷吉他，总共3500美元。

其实在每一个单元格，都使用了如下公式计算价值，对应上图的红色框。

 注意cell[i-1][j-当前商品重量]中的[i-1]而不是[i]因为，i代表本行商品，已经装入。

特性

• 在不改变表格列的粒度时，增加商品，不需要重新计算表格，往下继续算即可；
• 行的排列顺序不影响最终结果；
• 每列从上到下，价值不可能减小；
• 要么考虑拿走整件商品，要么考虑不拿，而没法判断该不该拿走商品的一部分（拿一部分应该用贪心）；
• 仅当每个子问题都是离散的，即不依赖于其他子问题时，动态规划才管用（旅行规划为例）；
• 大背包至多含有两个子背包，但子背包可能又含有子背包；
• 最优解可能出现在背包没装满的情况；

标题当增加一个重量为0.5的商品项链时，需要调整表格的粒度，重新计算 

以寻找最长公共子串为例应用动态规划

最长公共子串要求在原字符串中是连续的，而子序列只需要保持相对顺序一致，并不要求连续。

用户输入HISH，备选单词FISH、VISTA

Tips：

• 每种动态规划解决方案都涉及网格；
• 单元格中的值通常就是要优化的值。在前面的背包问题中，单元格的值为商品的价值；
• 每个单元格都是一个子问题，因此应考虑如何将问题分成子问题，这有助于找出网格的坐标轴

 对于寻找最长公共子串问题

• 单元格中的值即需要优化的值：最长公共子串的长度
• 横坐标，输入单词
• 纵坐标，可能匹配的单词
• 逐行计算，当cell[i][j]的i和j对应的字母不同，则该单元格为0；当相同，该单元格为1+cell[i-1][j-1]
• 整个表格填充完后寻找表格中的最大值

对于寻找最长公共子序列问题

• 当两字母相同时，值为左上角加1，这点比较好理解
• 当两字母不同时，值为上方和左侧中值大的，这是为了保存当前已经寻找到的最长子序列的长度，如此才能使下一次找到两个相同字母时，其左上角的值是正确的

 没有放之四海皆准的计算动态规划解决方案的公式.

---

第10章 KNN

非常简要地介绍了KNN、推荐系统、OCR等，因为已经了解且这里介绍的太基础，所以不详细记录。

---

第11章 What's next

这一章也语焉不详，不作记录。

树：B树，红黑树，堆，伸展树

反向索引；傅里叶变换；并行算法，mapreduce；概率型算法-布隆过滤器和HyperLogLog；安全散列算法SHA；Diffie-Hellman密钥；线性规划。

---

代码

代码1 Python实现快排

def q_sort(l):
    if len(l) == 2:
        if l[0] > l[1]:
            return [l[1], l[0]]
        else:
            return l
    elif len(l) == 1 or len(l) == 0:
        return l
    else:
        base_num = l[0]
        bigger_l = []
        smaller_l = []
        for i in l:
            if i < base_num:
                smaller_l.append(i)
            elif i > base_num:
                bigger_l.append(i)
        return q_sort(smaller_l) + [base_num] + q_sort(bigger_l)

代码2  使用狄克斯特拉算法找到权重最短的路径和其权重值

# 创建图
graph = {}
graph['Start'] = {}
graph['Start']['A'] = 5
graph['Start']['B'] = 0
graph['A'] = {}
graph['A']['C'] = 15
graph['A']['D'] = 20
graph['B'] = {}
graph['B']['C'] = 30
graph['B']['D'] = 35
graph['C'] = {}
graph['C']['End'] = 20
graph['D'] = {}
graph['D']['End'] = 10

inf = float("inf")

cost = {}
parents = {}
processed = []
# 原本是遍历graph的键，将其作为cost的键，并将值都设为inf，但是这种初始化不方便程序开始，所以手动初始化第一步的邻居
cost['A'] = 5
cost['B'] = 0
cost['C'] = inf
cost['D'] = inf
cost['End'] = inf
parents['A'] = 'Start'
parents['B'] = 'Start'
parents['C'] = None
parents['D'] = None
parents['End'] = None


# 寻找开支最小的节点
def find_min_node(cost, processed):
    temp = max(cost.values())
    node = None
    for k in cost:
        if k not in processed and cost[k] <= temp:
            node = k
            temp = cost[k]
    return node if node else None #都处理过就返回None


# 算法
Node = find_min_node(cost=cost, processed=processed) # 寻找最便宜节点
while Node:
    if Node == 'End':
        break
    for k in graph[Node]:
        temp_cost = cost[Node] + graph[Node][k]
        if temp_cost < cost[k]:
            cost[k] = temp_cost
            parents[k] = Node
    processed.append(Node)
    Node = find_min_node(cost=cost, processed=processed)


def p_path(e):  # 递归打印路径，因为时间仓促，没有仔细研究边界条件，所以不会打印最后的‘End’
    if e in parents.keys():
        print('^\n' + parents[e])
        return p_path(parents[e])

print('*'*10 + "\nCost:{c}\n".format(c=cost['End']) + '*'*10)
print('End')
p_path('End')

'''
结果：
**********
Cost:35
**********
End
^
D
^
A
^
Start

'''

代码3 使用贪婪算法解决集合覆盖问题

states = ['A', 'B', 'C', 'D', 'E', 'F', 'G']  # 州
r = {}  # 广播台
r['r1'] = ['A', 'C', 'F']
r['r2'] = ['B', 'C', 'D']
r['r3'] = ['C', 'E', 'G']
r['r4'] = ['A', 'G']

s = set(states)
covered = set()
r_selected = []

while s - covered:  # 还有未覆盖的
    k_selected = None
    l_temp = 0
    for k in r:  # 寻找能覆盖最多未覆盖地区的频道
        if k not in r_selected:
            temp = (s - covered) & set(r[k])  # 该频道能覆盖的未覆盖地区数
            if len(temp) > l_temp:
                l_temp = len(temp)
                k_selected = k
    covered = covered | set(r[k_selected])
    r_selected.append(k_selected)
print(r_selected)