双线性插值的公式推导及用克莱姆法则求解方程组

双线性插值的核心思想：将二维插值拆解为 “沿 X 轴的一维线性插值” 和 “沿 Y 轴的一维线性插值” 两步，最终通过代数运算合并得到统一公式。

一、一维线性插值

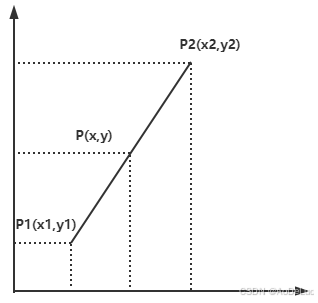
若已知两点 (x1,y1​) 和 (x2​,y2)，对任意点 x∈[x1,x2] 求y值，则根据两点求直线 斜率相同，得

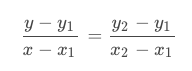
整理成如下格式，得任意点的y值为：

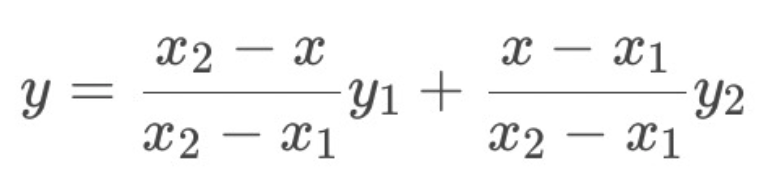
（本质是 “加权平均”，权重与点到端点的距离成反比）

二、二维线性插值

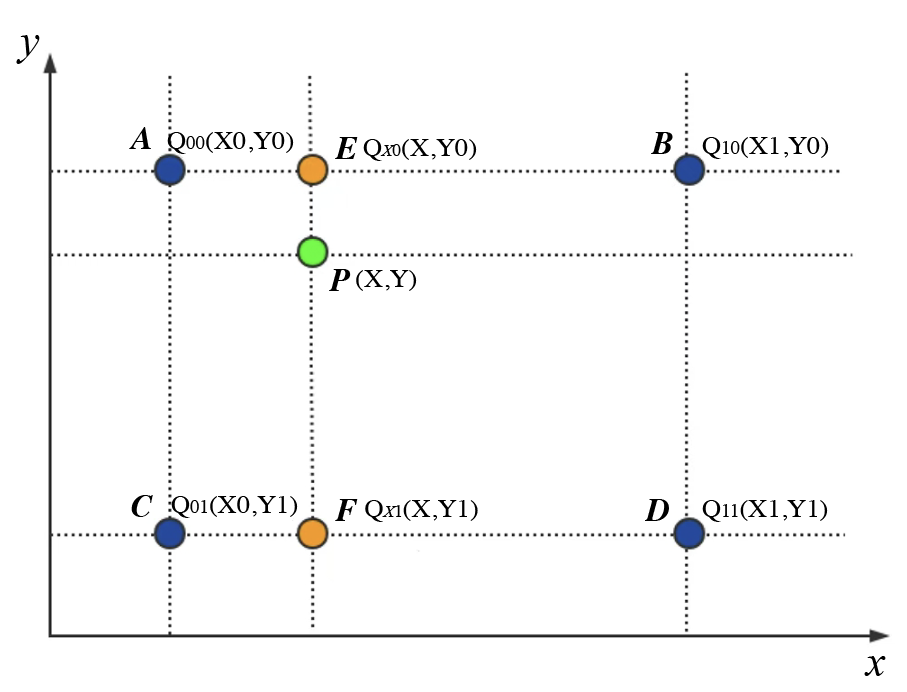
• 已知矩形网格的 4 个顶点坐标及对应的 Q 值：
  左上角 A(X0​,Y0​,Q00​)、右上角 B(X1​,Y0​,Q10​)、左下角 C(X0​,Y1​,Q01​)、右下角 D(X1​,Y1​,Q11​)；
• 目标：求网格内部任意点 P(X,Y) 的 Q 值 Q(X,Y)。

第一步：沿 X 轴方向，固定 Y=Y₀和 Y=Y₁分别做一维线性插值

将一维线性插值公式应用到二维网格的 X 方向：

    1. 固定 Y=Y₀（上边缘 A-B）：求点 E(X,Y0​) 的 Q 值 Qx0​
此时 x 的范围是 [X0​,X1​]，已知 A (X₀,Y₀,Q₀₀) 和 B (X₁,Y₀,Q₁₀)，代入一维公式：

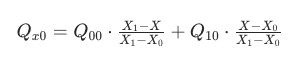
为简化书写，定义X 方向权重系数：​，则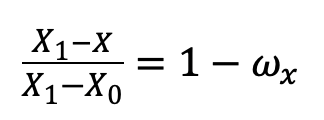，公式可改写为：
                                   (1)

    2.固定 Y=Y₁（下边缘 C-D）：求点 F(X,Y1​) 的 Q 值 Qx1​（注：F和E的X值相同）
同理，已知 C (X₀,Y₁,Q₀₁) 和 D (X₁,Y₁,Q₁₁)，代入一维公式并引入相同的：

                                    (2)

第二步：沿 Y 轴方向，固定 X，对 Qx0和 QX1做一维线性插值

已得 “同一竖直线 X 上、Y₀和 Y₁两个高度” 的 Q 值（Qx0​和Qx1​）；接下来利用E、F点的Q值沿 Y 轴插值，即可得到目标点 P (X,Y) 的 Q 值。

首先定义Y 方向权重系数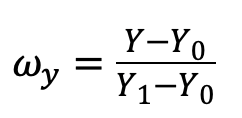：，则。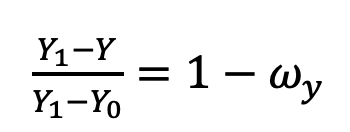
对 Qx0​（Y=Y₀）和 Qx1​（Y=Y₁）应用一维线性插值公式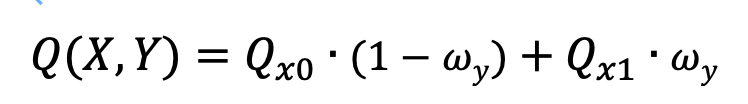：                           (3)

第三步：合并公式，得到双线性插值的最终形式

将式 (1) 和式 (2) 代入式 (3)，展开：

即为双线性插值的加权平均形式——目标点的Q值是4个顶点Q值的加权和，权重由点P到各顶点的相对位置决定（权重系数 ,∈[0,1]，确保插值结果在4个顶点Q值的范围内）。

若进一步将 ​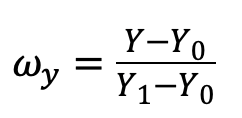、 代入，可展开为含X、Y的多项式形式：

其中 a,b,c,d 是由4个系数，可由顶点坐标和Q值确定。（类似一维线性插值y=kx+b的k和b可由2点确定）

三、利用双线性插值公式，及克莱姆法则解线性方程组

如上述，网格内 Q 值随 X、Y 坐标的变化遵循 “双线性函数关系”，即 可令Q (X,Y) 表示为一个包含 X、Y 线性项及交叉项的二元函数：

a,b,c,d 为4个待求系数，将4个网格顶点的坐标和Q值代入可得4个方程，写成矩阵的形式即：

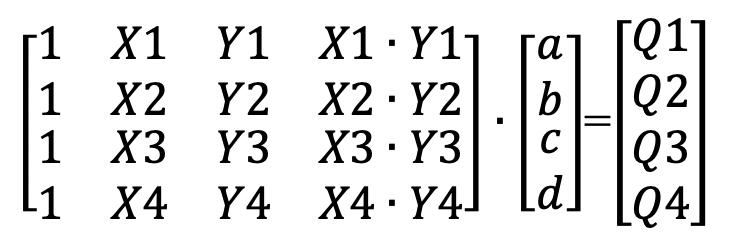
其中4个已知的网格顶点坐标是(X1,Y1) (X2,Y2) (X3,Y3) (X4,Y4)，4个点的Q值分别是Q1, Q2, Q3, Q4。

利用克莱姆法则求解：

先计算矩阵A的行列式为

克莱姆法则：若线性方程组的系数矩阵可逆（非奇异），即系数行列式 det(A)≠0，则线性方程组有唯一解，其解为

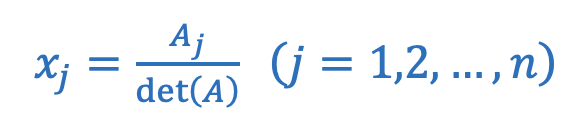
其中是把中第列元素对应地换成常数项(的)而其余各列保持不变所得到的行列式。

因此可直接得

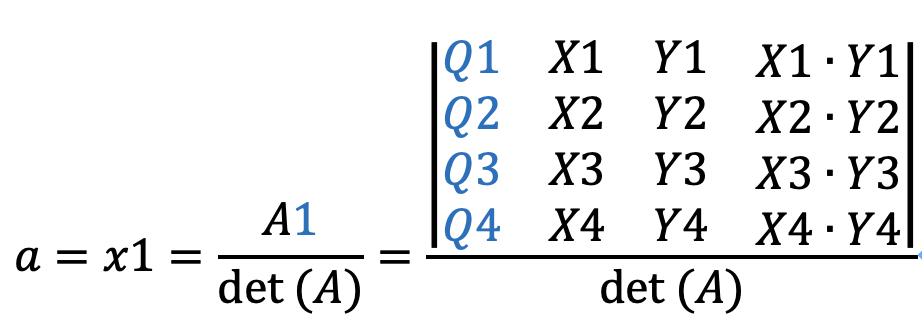
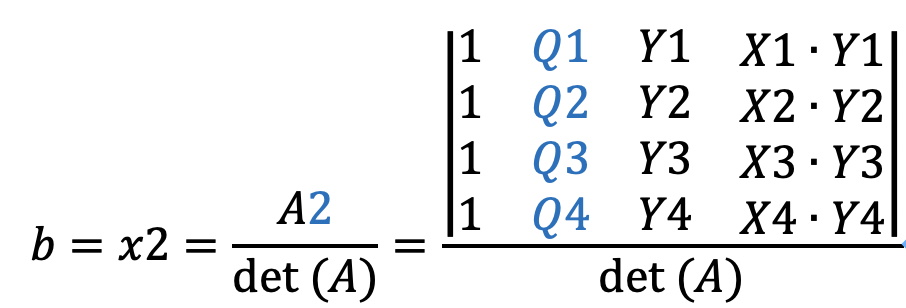
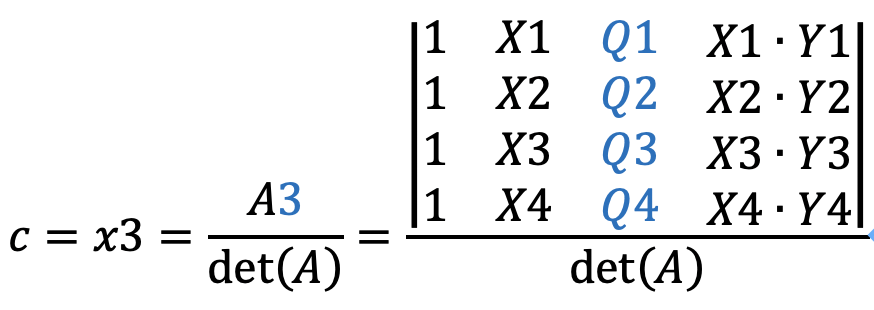
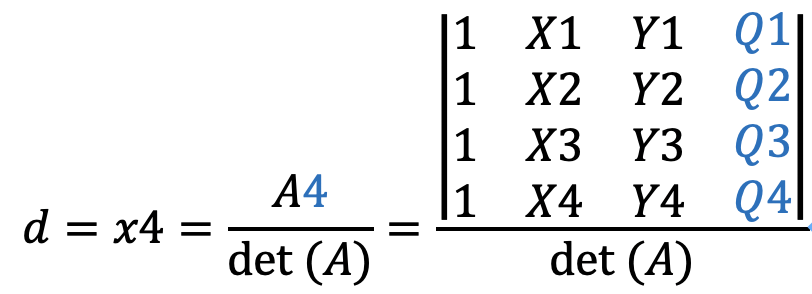
得到了a,b,c,d则函数已知，带入任意(X,Y)即可得到该点的值Q(X,Y)。