给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
示例 1:
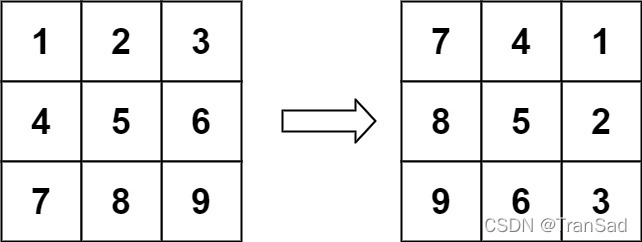
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
示例 2:
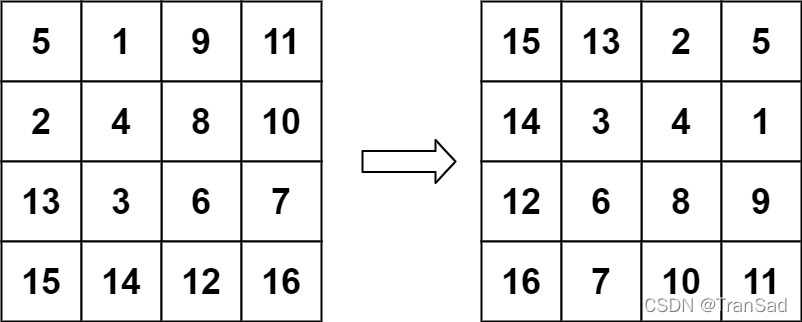
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
示例 3:
输入:matrix = [[1]]
输出:[[1]]
示例 4:
输入:matrix = [[1,2],[3,4]]
输出:[[3,1],[4,2]]
思路:
旋转矩阵有两类解决办法,但是每一类方法都不是一下子可以想出来的,还是说要对套路有个印象。
第一类是常规办法,我们得知道顺时针旋转矩阵等价于:先把矩阵转置,再每一行倒置。知道这一点后,再对矩阵操作就可以了。
第二类方法,用了python的zip操作,zip操作是一个对于列表进行压缩或者合并的操作。如对于给定矩阵:matrix = [[1,2],[3,4]],我们使用zip(*matrix),可以得到[(1,3),(2,4)]。
通过一定的实践后,直接上结论:
逆时针旋转:matrix[:] = zip(*matrix)[::-1] 先zip,再逆序
顺时针旋转:matrix[:] = zip(*matrix[::-1]) 先逆序,再zip
注意:zip 方法在 Python 2 和 Python 3 中的不同:在 Python 3.x 中为了减少内存,zip() 返回的是一个对象。如需展示列表,需手动 list() 转换。
即python3中,一般是list(zip())配合使用。
代码:
法1
class Solution(object):
def rotate(self, matrix):
#法1:三次逆时针 等于一次顺时针
for i in range(3):
#一次逆时针,先zip再逆序
matrix[:]=zip(*matrix)[::-1]#原地修改 加上[:]法2
class Solution(object):
def rotate(self, matrix):
#一次顺时针 先逆序 再zip
matrix[:]=list(zip(*matrix[::-1]))法3
class Solution(object):
def rotate(self, matrix):
row,col=len(matrix),len(matrix[0])
for i in range(row):
for j in range(i+1,col):
matrix[i][j],matrix[j][i]=matrix[j][i],matrix[i][j]
for i in range(row):
matrix[i]=matrix[i][::-1]小结:
注意,这个题也是要求我们原地修改矩阵,所以要用切片来完成。
法3应该是我们优先采用的标准做法,中规中矩的实现。
法1法2可以作为扩展和炫技使用~

























 5113
5113

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










