机器学习算法之K近邻

K近邻法(k-nearest neighbors,KNN)是一种很基本的机器学习方法了，通过测量不同特征值之间的距离的方法进行分类。（换句话说就是在一个坐标系中，你要根据你获得数据的坐标判断是距离那个点近。）

KNN做回归和分类的主要区别在于最后做预测时候的决策方式的不同。KNN做分类预测时，一般是选择多数表决法，即训练集里和预测的样本特征最近的K个样本，预测为里面有最多类别数的类别。而KNN做回归时，一般是选择平均法，即最近的K个样本的样本输出的平均值作为回归预测值。由于两者区别不大，虽然本文主要是讲解KNN的分类方法，但思想对KNN的回归方法也适用。

KNN算法要素

KNN算法我们主要要考虑三个重要的要素，对于固定的训练集，只要这三点确定了，算法的预测方式也就决定了。这三个最终的要素是k值的选取，距离度量的方式和分类决策规则。其中最重要的就是K值的选取了。

对于k值的选择，没有一个固定的经验，一般根据样本的分布，选择一个较小的值，然后通过交叉验证选择一个合适的k值。

选择较小的k值，就相当于用较小的领域中的训练实例进行预测，训练误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是泛化误差会增大，换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合；

选择较大的k值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少泛化误差，但缺点是训练误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测器作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单。

使用欧拉距离公式计算 x 到 X_train 中每个样本的距离：

import numpy as np
import math
from collections import Counter

def kNN(k, X_train, y_train, x):
	#计算点到样本的距离
    distances = [math.sqrt(np.sum((x_train - x) ** 2) for x_train in X_train]
    nearest = np.argsort(distances)
	#对这 k 个距离最近的样本对应的标记进行统计，找出占比最多标记即为 x 的预测分类，此例的预测分类为0：
    topK_y = [y_train[i] for i in nearest[:k]]
    votes = Counter(topK_y)
    return votes.most_common(1)[0][0]

也可以使用曼达顿距离公式：

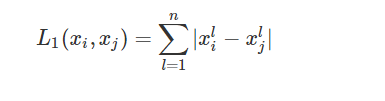
闵可夫斯基距离：

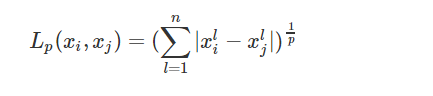
其实从这三个公式中看一看出欧氏距离是另外两个公式的特殊值情况。不过大多数情况下，欧式距离可以满足我们的需求，我们不需要再去操心距离的度量。

Scikit Learn 中的 k-近邻算法

一个典型的机器学习算法流程是将训练数据集通过机器学习算法训练（fit）出模型，通过这个模型来预测输入样例的结果。

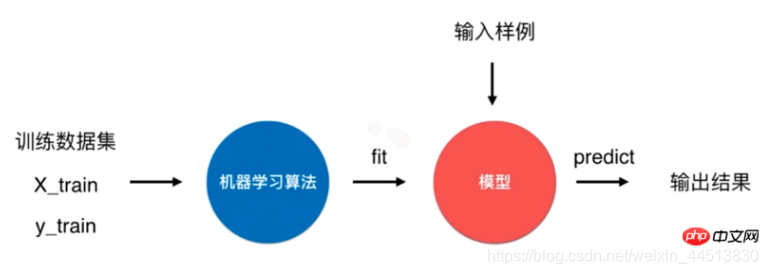
对于 k-近邻算法来说，它是一个特殊的没有模型的算法，但是我们将其训练数据集看作是模型。

Scikit Learn 中 k-近邻算法使用

Scikit Learn 中 k-邻近算法在 neighbors 模块中，初始化时传入参数 n_neighbors 为 6，即为上面的 k：

from sklearn.neighbors import KNeighborsClassifier
kNN_classifier = KNeighborsClassifier(n_neighbors=6)

fit() 方法根据训练数据集“训练”分类器，该方法会返回分类器本身：

kNN_classifier.fit(X_train, y_train)

predict() 方法预测输入的结果，该方法要求传入的参数类型为矩阵。因此，这里先对 x 进行 reshape 操作：

X_predict = x.reshape(1, -1)
y_predict = kNN_classifier.predict(X_predict)

实现 Scikit Learn 中的 KNeighborsClassifier 分类器

定义一个 KNNClassifier 类，其构造器方法传入参数 k，表示预测时选取的最相似数据的个数：

class KNNClassifier:
    def __init__(self, k):
        self.k = k
        self._X_train = None
        self._y_train = None

fit() 方法训练分类器，并且返回分类器本身：

def fit(self, X_train, y_train):
    self._X_train = X_train
    self._y_train = y_train
    return self

predict() 方法对待测数据集进行预测，参数 X_predict 类型为矩阵。该方法使用列表解析式对 X_predict 进行了遍历，对每个待测数据调用了一次 _predict() 方法。

def predict(self, X_predict):
    y_predict = [self._predict(x) for x in X_predict]
    return np.array(y_predict)
    
def _predict(self, x):
    distances = [math.sqrt(np.sum((x_train - x) ** 2)) for x_train in self._X_train]
    nearest = np.argsort(distances)
    topK_y = [self._y_train[i] for i in nearest[:self.k]]
    votes = Counter(topK_y)
    return votes.most_common(1)[0][0]

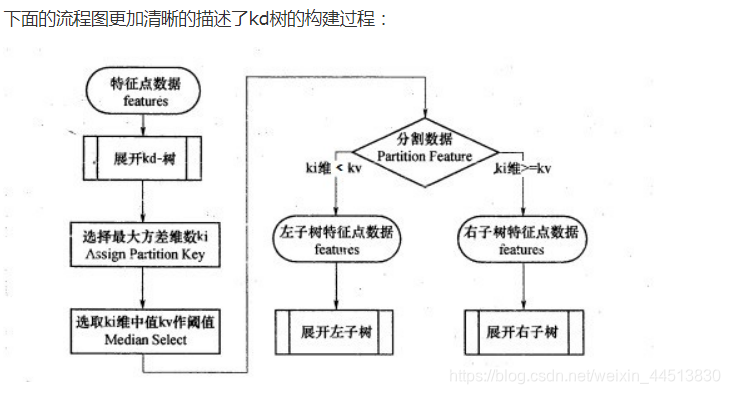
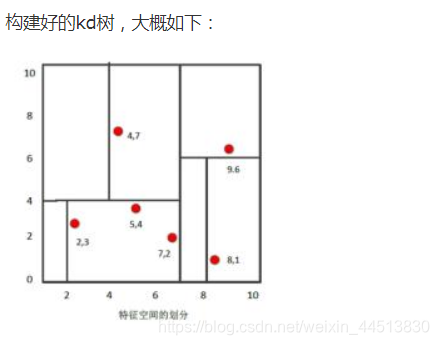
Kd树

KD数算法我认为他就是构建了一个搜索二叉树，每次都是从叶子节点出发，向上遍历，以此进行递归，从中得到距离值，最终得出属于哪部分节点。

KD树算法没有一开始就尝试对测试样本分类，而是先对训练集建模，建立的模型就是KD树，建好了模型再对测试集做预测。所谓的KD树就是K个特征维度的树，注意这里的K和KNN中的K的意思不同。KNN中的K代表特征输出类别，KD树中的K代表样本特征的维数。为了防止混淆，后面我们称特征维数为n。

KD树算法包括三步，第一步是建树，第二部是搜索最近邻，最后一步是预测。

KNN算法小结

KNN算法是基本的分类和回归方法，它非常容易学习，在维度很高的时候也有很好的分类效率，因此运用也很广泛。同时因为在相关机器学习包中就有相应的模块sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None)
其中最重要的参数就是n_neighbors，也就是所谓的K值，一般采用交叉验证法进行K值的调参。其他参数相关信息，可以参考sklearn文档

这里总结下KNN的优缺点。

KNN的主要优点有：
1） 理论成熟，思想简单，既可以用来做分类也可以用来做回归
2） 可用于非线性分类
3） 训练时间复杂度比支持向量机之类的算法低，仅为O(n)
4） 和朴素贝叶斯之类的算法比，对数据没有假设，准确度高，对异常点不敏感
5） 由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合
6）该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分

KNN的主要缺点有：
1）计算量大，尤其是特征数非常多的时候
2）样本不平衡的时候，对稀有类别的预测准确率低
3）KD树，球树之类的模型建立需要大量的内存
4）使用懒散学习方法，基本上不学习，导致预测时速度比起逻辑回归之类的算法慢
5）相比决策树模型，KNN模型可解释性不强

Deom

def knncls():
    """
    K-近邻算法预测用户查询的业务
    :return:
    """
    data = pd.read_csv("./data/FBlocation/train.csv")

    # print(data)
    # 1、缩小数据数据范围
    data = data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75")

    # 3、把签到位置小于N个人的位置给删除掉

    # 4、 分割数据集到训练集合测试集
    # 取出特征值和目标值
    y = data['place_id']

    x = data[['x', 'y', 'accuracy', 'time']]

    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3)

    # 进行数据的标准化处理
    std = StandardScaler()

    # 对训练集的特征值做标准化处理
    x_train = std.fit_transform(x_train)

    # 对测试集的特征值做标准化处理
    x_test = std.fit_transform(x_test)

    # 5、 利用K近邻算啊去进行训练预测
    # knn = KNeighborsClassifier(n_neighbors=1)
    #
    # # 代用fit和predicthuozhe score
    # knn.fit(x_train, y_train)
    #
    # # 预测测试集的办的业务类型
    # y_predict = knn.predict(x_test)
    #
    # print("K近邻算法预测的这些时间的业务类型：", y_predict)
    #
    # print("k近邻预测的准确率为：", knn.score(x_test, y_test))

    # 应用网格搜索+交叉验证对K-近邻算法进行调优
    knn = KNeighborsClassifier()

    # 构造超参数的字典
    # 对knn来讲，数据量比较大，k = 根号(样本)
    param = {"n_neighbors": [1, 3, 5, 7, 10]}

    # 为了看到效果不多，cv=2，通常会选择10
    gc = GridSearchCV(knn, param_grid=param, cv=2)

    # fit输入数据
    gc.fit(x_train, y_train)

    # 查看模型超参数调优的过程，交叉验证的结果
    print("在2折交叉验证当中的最好结果:", gc.best_score_)
    print("选择的最好的模型参数是：", gc.best_estimator_)
    print("每次交叉验证的验证集的预测结果：", gc.cv_results_)

    # 预测测试集的准确率
    print("在测试集当中的最终预测结果为：", gc.score(x_test, y_test))

    return None