【模拟电子技术Analog Electronics Technology 14】——集成运放中的单元电路 之 集成运放的输入级：长尾式差放各种接法的参数分析

1. 多级放大电路的耦合方式

这里只做了解：

1. 直接耦合放大电路
2. 阻容耦合放大电路
3. 变压器耦合放大电路
4. 光电耦合

1.1 多级放大电路的动态分析

一个N级的放大电路的放大倍数的求法：$$A_u=A_{u1}\ast A_{u2}\ast \cdots \ast A_{un}$$
多级放大电路的输入电阻等于第一级的输入电阻：$R_i=R_{i1}$
多级放大电路的输出电阻等于最后一级的输出电阻：$R_0=R_{0n}$

2.集成运放概述

2.1 集成运放的结构特点

这部分大家可以自己看看书上的部分自学

2.2 集成运放中的单元电路

2.2.1 零点漂移现象

即输入为0，输出不为0的情况，原因有电源电压的不稳定、元器件的老化，三极管的温度的敏感
其中，三极管的温度特性的主要因素

2.2.2 差分放大电路

既然单管的直接耦合连接会产生零点漂移，那么引入了对称的两部分，就会使得两边产生的相同的零点漂移电压相互抵消，从而改善了零点漂移的问题

2.2.3 （重要！）长尾式放大电路

2.2.3.1静态分析

静态电路中，$u_{i1},u_{i2}$相当于接地，那么，我们就重点从左下方的回路切入：$$R_{b1}{I}_{BQ}+U_{BEQ}+2I_{EQ}{R}_e=V_{EE}$$
即：$$R_{b1}\frac{I_{EQ}}{1+\beta }+U_{BEQ}+2I_{EQ}{R}_e=V_{EE}$$
从而可以解出$I_{EQ}$
求$U_{CEQ}$，有个技巧，我们可以分别计算一下$U_{CQ}$和$U_{EQ}$
那么，$U_{CEQ}=U_{CQ}-U_{EQ}$
在上图的例子里面，$U_{CQ}=V_{CC}-I_{CQ}{R}_{c1}$
$U_{EQ}=2I_{EQ}{R}_e-V_{EE}$(解出来$U_{EQ}$如果有负号要保留！）

【下面注意在输出端带载情况下$U_{CQ}$的计算】：

这种情况下，$U_{CQ}$的计算和上面空载情况的有所不同，这里我们需要用戴维宁等效来做：
等效电路如下：

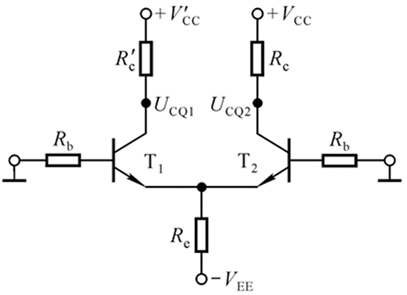
其中，我们重点关注的就是$V_{CC}^{\prime }$和$R_c^{\prime }$：$$\begin{gathered} V_{CC}^{\prime }=\frac{R_L}{R_L+R_c}{V}_{CC} \\ {R}_c^{\prime }=R_L//R_c \end{gathered}$$
因此，此时的$U_{CQ}=V_{CC}^{\prime }-I_{CQ}{R}_c^{\prime }$
【特别警告】：没有连负载的那边，电压和等效电阻都是不变的，就还是$V_{CC}$和$R_c$！！

2.2.3.2 动态分析

首先，我们要知道在长尾式放大电路中有几种输入成分：
【1】：共模成分
对于上面的长尾式放大电路而言，当输入信号$u_{I1},u_{I2}$大小相等，极性相同时，我们称之为共模信号
即：$u_{I1}=u_{I2}=u_{Ic}$（其中c代表common）
其中双输出的长尾式放大电路对共模信号有抑制作用，因为我们的输出$u_0$是$u_{c2}$和$u_{c1}$的电位差，但是由于电路的结构和参数都对称，因此，$u_0=u_{c2}-u_{c1}=0$
其中特别注意：$零点漂移对差放而言就相当于一对共模信号！$
$同时，由于温度变化引起的变化等效也被认为是共模信号$

但是，在工程上，虽然做到电路的结构对称很简单，但是电路元件的参数完全一样几乎不可能，因此，实际的差放对于共模量的抑制不完全，这怎么办呢？请注意电路下方有一个$R_e$，它相当重要，对共模信号的负反馈很强，因为共模信号两次经过$R_e$，它的负反馈原理和之前一样

在分析动态参数之前，我们得分两种情况，分为了双输出和单输出两种情况：

1. 双输出：我们可以直接看上面的图，这种情况下，$u_0$ = 0，$A_c=\frac{u_0}{u_{I}c}=0$
   要求双输出的输出电阻，我们从输出端往里看进去，发现是$R_{c1}$和$R_{c2}$的串联，因此，输出电阻为：$R_{oc}=2R_c$

2. 单输出：我们看看下面的图：

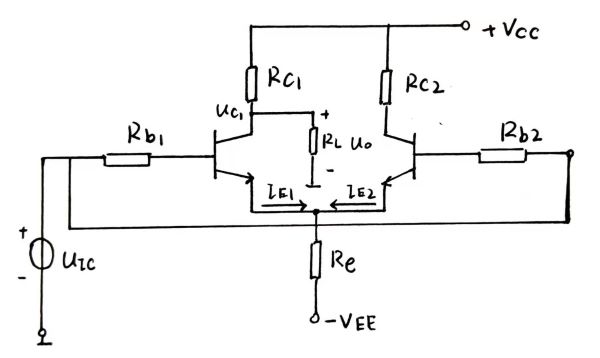
先从$A_c$的表达式入手：$$A_c=\frac{u_0}{u_{Ic}}$$
我们发现这不就是单管的放大倍数嘛！
但是，下面我们要处理一件事情，就是$R_e$在单管中到底是多大？
首先，我们明确一件事情：就是如果想将$R_e$等效到单管上，那么$R_e$在原本电路的压降要等于等效到单管之后对应位置那个电阻的压降，那么，我们看看原本电路中$R_e$上的压降：
$$u_{R_e}=2I_E{R}_e$$
而当$R_e$等效成单管的射极电阻后，射极电阻的压降仍然要为：$2I_E{R}_e$，而此时，单管的射极电流为$I_E$了，因此，$R_e$等效成单管电阻之后应该变为2$R_e$

既然我们了解了等效之后电路的各个元件参数，那么后面求$A_c$就和Chapter2里面的方法一样了：

因此，我们来看看:

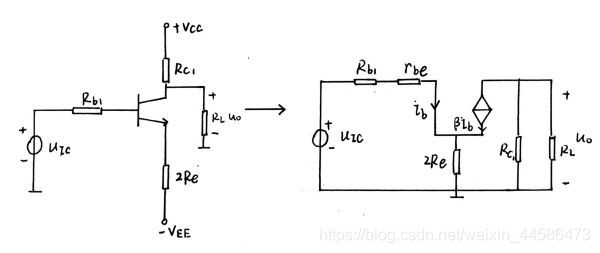
这是不是相当熟悉了：$$A_c=\frac{-\beta I_b(R_c//R_L)}{I_b(R_{b1}+r_{be})+2(1+\beta )I_b{R}_e}=\frac{-\beta (R_c//R_L)}{R_{b1}+r_{be}+2(1+\beta )R_e}$$
我们希望共模放大倍数越小越好，这样一来对共模信号的抑制能力越强，因此$A_c$应该小一点，做法是将$R_e$取得很大，有时候可以用电流源代替（在交流通路中电流源内阻相当大）

输出电阻为$R_{oc}=R_c$

【2】：差模成分
当两个输入大小相等，极性相反时，我们称之为差模信号；即：$u_{I1}=-u_{I2}=\frac{u_{Id}}{2}$
我们来看看电路图：

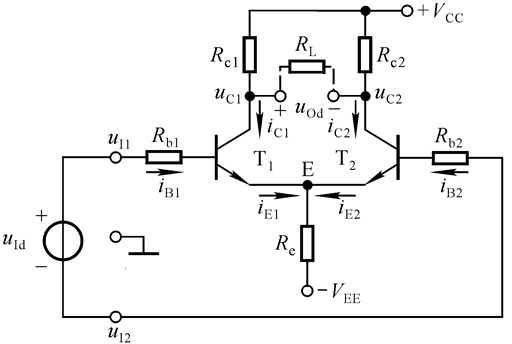
同样的，在分析输入为差模信号的动态参数前，我们也分成两种情况讨论：1. 双输出 2.单输出

1. 对于双输出的情况，即上图情况：$$A_d=\frac{u_{od}}{u_{Id}}=\frac{u_{od1}-u_{od2}}{2u_{Id1}}=\frac{2u_{od1}}{2u_{Id1}}=\frac{u_{od1}}{u_{Id1}}$$
   我们惊喜地发现，这不就是单管的放大倍数嘛！
   那么，我们来分析一下：在差模信号中，流过$R_e$的电流大小相等，方向相反，因此，$R_e$的电位为0，又由于$u_{c1},u_{c2}$的电位大小相等，方向相反，因此，$R_L$的中点处相当于零电位点，刚刚我们不是说对于差分信号，双出的放大倍数相当于单管嘛，那么，对于单个管子，其负载就应该为$\frac{1}{2}{R}_L$
   那么，我们应该可以口算出来$A_u$:$$A_u=\frac{-\beta (R_c//\frac{1}{2}{R}_L)}{R_b+r_{be}}$$
   同时，对于差模信号双输出的输入电阻$R_{id}=2(R_{b1}+r_{be})$
   要求输出电阻的话，我们就从输出端往里看，是$R_{c1}$和$R_{c2}$的串联，因此，双输出的输出电阻为$R_{od}=2R_c$

2. 对于单输出的情况：

我们先分析一下放大倍数的表达式：$$A_u=\frac{u_0}{2u_1}=\frac{1}{2}\frac{u_0}{u_1}$$
我们惊喜地发现这是单管放大倍数的一半，但是，有一点不同的是，此时用单管计算时，负载就是$R_L$，因此，我们可以得到：$$A_u=\frac{1}{2}\frac{-\beta (R_c//R_L)}{R_b+r_{be}}$$
同样的，对于差模信号单输出的输入电阻$R_{id}=2(R_{b1}+r_{be})$
输出电阻为$R_c$

Tips: 1. 如果$R_L$接在了右边的输出端，那么此时的放大倍数$A_u$无负号
2. 当$R_c$无穷大时，差模信号单出和双出的放大倍数基本相等

至此，对于共模信号的单出和双出，差模信号的单出和双出都分析完了，来总结一下：
对于双输出：
$$A_c=0$$
$$A_d=\frac{-\beta (R_c//\frac{1}{2}{R}_L)}{R_b+r_{be}}$$
$$输出电阻R_0=2R_c$$
对于单输出：
$$A_c=\frac{-\beta (R_c//R_L)}{R_b+r_{be}+2(1+\beta )R_e}$$
$$A_d=\frac{1}{2}\frac{-\beta (R_c//R_L)}{R_b+r_{be}}$$
$$输出电阻R_0=R_c$$

对于任意接法，输入电阻均为：
$R_i=2(R_b+r_{be})$

3. 复习Chapter 3时的再总结：

1. 假如有一个由长尾式放大电路组成的多级放大电路，如果题目说一开始存在零零点漂移，问应该怎么调节电阻？

那么做法是：我们就写出长尾式放大电路那一级的共模放大倍数（该级电路的负载电阻直接用$R_L$表示），然后，我们就需要使得共模放大倍数越小越好，因此就可以根据$A_c$看出应该怎么调节电阻大小

2. 遇到长尾式放大电路、电流源电路和互补输出级构成的电路，分析步骤是：
   （1）先标出每一级输出的极性（这样到时候我们才能正确标出电流的流向）
   （2）画微变等效（电流源电路直接当地了，然后我们的互补输出级也只需要取上半部分或者下半部分其中之一画出来就行），计算的时候一定要注意：每一级的负载电阻都是后一级电路的输入电阻

3. 集成运放的组成部分（可能考填空）：输入级、中间级、输出级和偏置电路

4. 共模信号和差模信号的求法：已知两个输入$u_{I1}$，$u_{I2}$，那么，共模输入就是：$\frac{u_{I1}+u_{I2}}{2}$，差模输入就是$u_{I1}-u_{I2}$