【信号与系统学习笔记】—— 一起走进“卷积”的世界3 【技巧方法篇】 连续时间信号的卷积计算技巧

相比于前两篇 $Blog$ 中关于卷积物理意义以及性质的讨论，这篇 $Blog$ 重点归纳卷积计算的技巧和方法。以连续时间信号的卷积计算为主，因为离散情况下很简单，慢慢滑动一个个对应着来就OK。因为连续时间信号的卷积涉及积分，对上下限的考量需要对卷积定义比较清晰才行

典型例题来袭

注：勘误！！下面的例题中，关于 $h(-\tau )$ 的函数波形，在 $t=-2T$的时候的函数值应该为 $2T$

在着手开始分析第一个例子之前，我们回顾一下连续信号的卷积公式：$$y(t)={\int }_{-\infty }^{+\infty }x(\tau )h(t-\tau )d\tau$$
其中，$x(\tau )$ 和 $h(t-\tau )$ 代表两者的重叠部分，具体的值是两个重叠部分函数值的乘积。 $\tau$ 应该是两者重叠部分的时间范围

其实，这个表达式是一个囊括了不同情况的综合表达式，很多时候，我们计算的卷积往往是分段函数，这时，积分的上下限就不能是简单的 $+\infty$ 和 $-\infty$了

【例题一】：求以下两个信号的卷积

$Step1$：先画出 $x(\tau )$ 和 $h(-\tau )$：

还记得我们在关于卷积的第一篇 $Blog$ 里面谈到的吗：$h(t-\tau )$ 代表的是对 $h(-\tau )$ 原点的移动，，具体把 $h(-\tau )$ 的原点移动到什么地方呢？就是看 $x(\tau )$ 图像中，我们要求的 $\tau =t$ 的位置

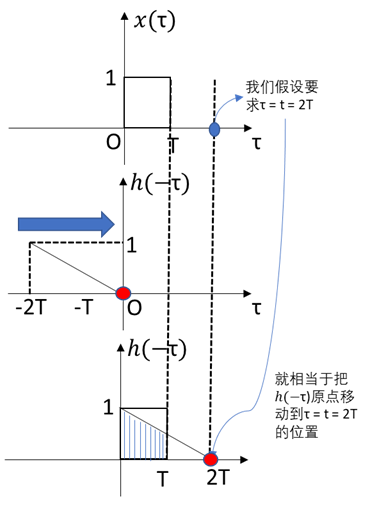
$Step2$：我们要大致观察以下 $t$ 取什么值的时候二者有重叠部分，取什么值的时候没有重叠部分
从本题，很明显，在 $t<0$，以及 $t>3T$ 的时候，二者没有重叠，因此也有：$y(t)=0$

而在 $0<t<T$；$T<t<2T$ 以及 $2T<t<3T$ 的部分都会有重叠，因此我们分别讨论。

（1）在 $0<t<T$ 时，

黄色区域是二者重叠部分，不过我们重点关系的，是这个重叠部分的范围，显然，是：$[0,t]$
因此，$\tau$ 的范围就是：$0<\tau <t$，在这个范围下，那条斜线就是 $h(t-\tau )$，横线就是 $x(\tau )$。那么我们可以知道：在此范围下，$x(\tau )=1$、$h(t-\tau )=-(\tau -t)$（因为 $h(t-\tau )$ 在本题中始终是一条斜率为 -1 ，始终过点 (t, 0) 的直线）

因此，我们就带入公式，得：$$y(t)={\int }_0^t-(\tau -t)d\tau =\frac{1}{2}{t}^2$$

至此，我们完成了第一个重叠区间的卷积积分的计算

对于 $T<t<2T$ 时，如下图所示：

黄色区域是重叠部分，重叠部分的范围是 $[0,T]$，因此，$0<\tau <T$，重叠区域两函数表达式和第一种情况一样，因此，我们有：$$y(t)={\int }_0^T-(\tau -t)d\tau =Tt-\frac{1}{2}{T}^2$$

后面的情况，处理方法一样，这里就不赘述啦。最终的结果和 $y(t)$ 的图像如下：

始终贯穿这一方法，卷积积分的计算也就不那么困难了！

好啦！这篇 $Blog$ 到这里就结束辽！和之前的两篇 $Blog$ 结合在一起，就成了 “卷积三剑客”。希望这三篇 $Blog$ 能对今后卷积的学习带来帮助！

“卷积笔记三剑客地址”：

【信号与系统学习笔记】—— 一起走进“卷积”的世界 1【详细整理+个人理解】

【信号与系统学习笔记】—— 一起走进“卷积”的世界 2【系统基本性质和卷积的关系】

【信号与系统学习笔记】—— 一起走进“卷积”的世界3 【技巧方法篇】 连续时间信号的卷积计算技巧