【通信原理 入坑之路】—— 理解 4G，5G中的天王山：OFDM【学习笔记3】

在之前的博文中，我们以及了解了OFDM的基本原理与频谱特性，下面我们希望搞清楚理想情况下OFDM的框图是怎么样的：

我们首先假设各个子载波均采用相同的调制方式（以QPSK为例），看看发送的实OFDM基带信号：

这里特别值得注意的是：OFDM中我们所讲的“子载波” 指的是 $cos(k{\omega }_{0}t)$ 以及 $sin(k{\omega }_{0}t)$ ，并不是高频载波！因此下图中的 $s(t)$也只是基带信号。其频谱在上一篇博文中有详细的分析。

根据上面OFDM基带信号发射框图，我们可以很容易写出实OFDM基带信号的表达式： s ( t ) = I 1 c o s ( ω 0 t ) − Q 1 s i n ( ω o t ) + I 2 c o s ( 2 ω 0 t ) − Q 2 s i n ( 2 ω 0 t ) + ⋯ I N c o s ( N ω 0 t ) − Q N s i n ( N ω 0 t ) = ∑ k = 1 N [ I k c o s ( k ω 0 t ) − Q k s i n ( k ω 0 t ) ] = R e { ∑ k = 1 N [ ( I k + j Q k ) ( c o s ( k ω 0 t ) + j s i n ( k ω 0 t ) ] } = R e { ∑ k = 1 N [ I k c o s ( k ω 0 t ) − Q k s i n ( k ω 0 t ) ] + j ∑ k = 1 N [ Q k c o s ( k ω 0 t ) + I k s i n ( k ω 0 t ) ] } \begin{aligned} s(t) &= I_1cos(\omega_0t)-Q_1sin(\omega_ot)+I_2cos(2\omega_0t)-Q_2sin(2\omega_0t)+\cdots I_Ncos(N\omega_0t)-Q_Nsin(N\omega_0t)\\ &=\sum_{k=1}^N[I_kcos(k\omega_0t)-Q_ksin(k\omega_0t)]\\ &=Re\{\sum_{k=1}^N[(I_k+jQ_k)(cos(k\omega_0t)+jsin(k\omega_0t)]\}\\ &=Re\{\sum_{k=1}^N[I_kcos(k\omega_0t)-Q_ksin(k\omega_0t)] + j\sum_{k=1}^N[Q_kcos(k\omega_0t)+I_ksin(k\omega_0t)]\} \end{aligned} s(t)​=I1​cos(ω0​t)−Q1​sin(ωo​t)+I2​cos(2ω0​t)−Q2​sin(2ω0​t)+⋯IN​cos(Nω0​t)−QN​sin(Nω0​t)=k=1∑N​[Ik​cos(kω0​t)−Qk​sin(kω0​t)]=Re{k=1∑N​[(Ik​+jQk​)(cos(kω0​t)+jsin(kω0​t)]}=Re{k=1∑N​[Ik​cos(kω0​t)−Qk​sin(kω0​t)]+jk=1∑N​[Qk​cos(kω0​t)+Ik​sin(kω0​t)]}​

因此上面的步骤也可以简化写成这样：

即OFDM的基带信号现在是用 $(I_k+j{Q}_k)$ 和 $e^{j{\omega }_{0}t}$ 相乘的结果取实部。而众所周知，要想完成发送的过程，其实还需要将这个基带信号 $s(t)$ 调制到高频载波上。即如下图所示：

注意：高频载波的频率我们是用 ${\omega }_c$ 表示的，这也再次提醒：子载波和高频载波是两个东西！

而在实际中，我们在调制到高频中时，会把 $(I_k+j{Q}_k)$ 和 $e^{j{\omega }_{0}t}$ 相乘的结果的实部和虚部分别调制到 $I^{\prime }$ 路和 $Q^{\prime }$ 路两路正交的高频载波上，如下图：

因此整个 OFDM 的框图可以画成下图这样：

同时调制实部虚部的好处是带宽可以变为原来的一半，这个结论我们先不加证明地给出

了解了OFDM信号调制的框图，下面我们就上面的例子（子载波均已QPSK调制）来看看信号的时序图：

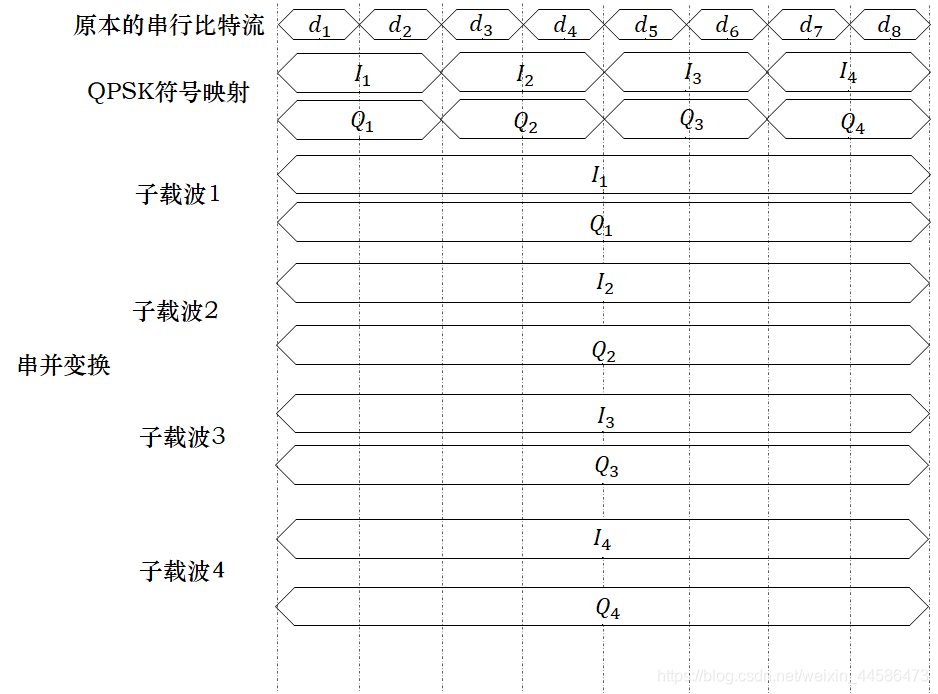我们举一个具体的例子来看看OFDM是如何利用子载波工作的：我们假设要传输的串行比特流是：0 0 0 1 1 1 1 0 . 然后根据QPSK的符号映射关系表，我们就可以得到 $I_1,I_2,I_3,I_4,Q_1,Q_2,Q_3,Q_4$。

如果我们假设四个子载波的频率分别为 ：1Hz, 2Hz, 3Hz, 4Hz。即：子载波1是$cos(2\pi 1t)$和$sin(2\pi 1t)$ ；子载波2是：$cos(2\pi 2t)$和$sin(2\pi 2t)$ ；子载波3是$cos(2\pi 3t)$和$sin(2\pi 3t)$ ；子载波4是：$cos(2\pi 4t)$和$sin(2\pi 4t)$ ；

figure;
t = 0:0.001:1;
I1 = 1/sqrt(2);  
Q1 = 1/sqrt(2);
s1 = I1*cos(2*pi*1*t) - Q1*sin(2*pi*1*t);
subplot(411);
plot(t, s1);
grid on;

I2 = -1/sqrt(2);
Q2 = 1/sqrt(2);
s2 = I2*cos(2*pi*2*t) - Q2*sin(2*pi*2*t);
subplot(412);
plot(t, s2);
grid on;

I3 = -1/sqrt(2);
Q3 = -1/sqrt(2);
s3 = I3*cos(2*pi*3*t) - Q3*sin(2*pi*3*t);
subplot(413);
plot(t, s3);
grid on;

I4 = 1/sqrt(2);
Q4 = -1/sqrt(2);
s4 = I4*cos(2*pi*4*t) - Q4*sin(2*pi*4*t);
subplot(414);
plot(t, s4);
grid on;

因此我们就可以得到4路经过调制的子载波的波形：

将四路子载波叠加起来就得到了一个OFDM符号，如下图所示：

figure;
t1 = s1+s2+s3+s4;
plot(t, t1);
grid on;

下面我们从立体的角度看看OFDM符号和这四个子载波的关系：(下图中加粗的绿色线表示OFDM符号）

figure;
y=ones(1,length(s1));
plot3(t,y,s1);
xlabel('x');
ylabel('y');
zlabel('z');
grid on;
hold on;

y2 = 2*ones(1,length(s2));
plot3(t,y2,s2);
xlabel('x');
ylabel('y');
zlabel('z');
hold on;

y3 = 3*ones(1,length(s3));
plot3(t,y3,s3);
xlabel('x');
ylabel('y');
zlabel('z');
hold on;

y4 = 4*ones(1,length(s4));
plot3(t,y4,s4);
xlabel('x');
ylabel('y');
zlabel('z');
hold on;

y5 = 5*ones(1,length(t));
plot3(t,y5,t1,'LineWidth',2);
xlabel('t');
ylabel('f');
set(gca,'ytick',[])

那么，多个OFDM符号在时域上组合起来，就构成了OFDM信号。 即OFDM符号相当于 OFDM信号这个长长铁链中的其中一个铁环。

---

利用多路的子载波，每一个OFDM符号上就可以承载多路信息，这些信息以基波周期（这里是1Hz载波为基波）发生变化。

在这个例子里面，我们原本1s可以传8个串行比特 $00101110$，即上图中的 $d_1-d_8$是一秒传完的。但是在串行比特流经过QPSK符号映射之后，就变成1s只能传输4个QPSK符号了，而在经过串并变换之后，每秒只能传输1个符号了。换句话说，从上图我们可以看出来，在一个基波周期内，OFDM子载波各个周期的振幅是一样的，即OFDM子载波在基波周期的时长内，都只传递一种信息。

上图的基波周期是 1s，本例中四次谐波在1s中虽然经历了4个周期，但是都只传递一种QPSK符号。而反过来看单载波系统，它每一个周期都可以传递不同的QPSK符号，如果我们在单载波系统中采用上图中的四次谐波，那么在这 1s 里面，这个单载波系统可以传递4个QPSK符号。而OFDM的子载波在同样 1s的时间内却只能传1个QPSK符号。这看起来有些不妙是吗？

虽然OFDM子载波在相同时间内的传输效率不如单载波，但是OFDM系统可以采用多个子载波，在同样1s的时间内，OFDM可以利用4个子载波同时传递QPSK符号，因此，尽管OFDM的符号率比较低，但是总体的传输效率和单载波是一致的。

导致这个重要差别的原因就是我们一开始OFDM框图里面所画的 “串并变换” ，它将原本高速的串行数据流变成若干低速的并行数据，

可是为什么要这样大费周章的进行串并变换呢？你OFDM最终总的传输效率还只是和单载波一样啊？

我们将在下一篇博客里面详细看看把高速串行信号转化成低速并行信号带来的好处。