数值积分
直接利用某些节点上的函数值计算积分值,将积分求值问题归结为函数值的计算,可概述为如下公式
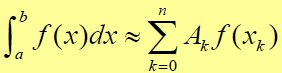
复化梯形公式

将区间n等分,每个小区间分别用梯形公式(两个节点)求积分,化简得到如上公式。
/**
*@name Cotes:复化梯形公式
*@param1 below:区间下限
*@param2 upper:区间上限
*@param3 n:划分子区间的个数
**/
double trapezoid(double below,double upper,int n)
{
double h=(upper-below)/n;
double x=below;
double S=0;
for (int i=1;i<n;i++)
{
//计算内部各节点的函数值 1~(n-1)
x+=h;
S+=function(x);
}
return (h/2)*(2*S+function(below)+function(upper));
}
复化辛普生公式

同样将区间n等分,每个小区间分别用辛普生公式(两个节点加上中点)求积分,化简得到如上公式。
/**
*@name Cotes:复化辛普生法
*@param1 below:区间下限
*@param2 upper:区间上限
*@param3 n:划分子区间的个数
**/
double Simpos(double below,double upper,int n)
{
double h=(upper-below)/n;
double S1=0;
double S2=function(below+h/2);
double x=below;
for (int i=1;i<n;i++)
{
//计算各节点处的函数值 1~(n-1)
x+=h;
S1+=function(x);
}
x=below+h/2;
for (int j=1;j<n;j++)
{
//计算各区间中点处的函数值 0.5~(n-0.5) 共n项
x+=h;
S2+=function(x);
}
return (h/6)*(function(below)+function(upper)+2*S1+4*S2);
}
复化柯特斯公式

同样将区间n等分,每个小区间分别用柯特斯公式(两个节点加上三个四等分点)求积分,化简得到如上公式。
/**
*@name Cotes:复化柯特斯公式
*@param1 below:区间下限
*@param2 upper:区间上限
*@param3 n:划分子区间的个数
**/
double Cotes(double below,double upper,int n)
{
double h=(upper-below)/n;
double S1=0;
double S2=0;
double S3=0;
double S4=0;
double x=below;
x=(below+h/4);
for (int i=0;i<n;i++)
{
//计算各区间1/4处的值 1/4~(n-3/4)共n项
S1+=function(x);
x+=h;
}
x=(below+h/2);
for (int i=0;i<n;i++)
{
//计算各区间1/2处的值 1/2~(n-1/2)共n项
S2+=function(x);
x+=h;
}
x=below+3*h/4;
for (int i=0;i<n;i++)
{
//计算各区间3/4处的值 3/4~(n-1/4)共n项
S3+=function(x);
x+=h;
}
x=below+h;
for (int i=1;i<n;i++)
{
//计算各区间3/4处的值 1~(n-1)共n-1项
S4+=function(x);
x+=h;
}
return (h/90)*(7*function(below)+32*S1+12*S2+32*S3+14*S4+7*function(upper));
}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








