单纯形算法及对偶的python实现

单纯形算法

使用python编程语言通过矩阵运算编程来实现单纯形算法。

1.建立模型后输入数据列出初始单纯形表

将线性规划问题转化为标准型，求minz转化为求max-z
以下图为例

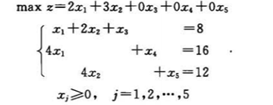
初始化

import numpy as np
class Simplex(object):
    #构造函数（初始化函数）
    def __init__(self,z,B,bound):  
        self.X_count=len(z)          #变量个数
        self.b_count=len(bound)      #约束条件个数
        self.z=z                     #目标函数
        self.C=[]                    #检验数
        self.B=B                     #基变量,由于运算规则必须按顺序给出基变量
        self.bound=bound             #约束条件,包括右端常数
        self.flag=0                  #解的类型，0为（暂时）无解，1为唯一最优解，2为无穷多最优解
        self.special=True            #无界解

2.进行最优性检验

计算所有的检验数，若所有的检验数都小于零，结束得到最优解，否则转下步。若检验数大于零而Pk<=0（θ无值可计算）,此问题属于无界解，结束，否则转入下一步。

    def Iteration(self):    	
        lim=100		#防止无限迭代
        while(lim>0):
            self.C=[] #检验数清空
            for j in range(self.X_count):     
                zj=0
                for i in range(self.b_count): #遍历第j列全行系数，计算第j个变量检验数
                    zj+=self.bound[i][j]*self.z[self.B[i]]#限制B基变量序号顺序之处
                self.C.append(self.z[j]-zj) #检验数,'cj-zj'
            self.Check() #判断迭代是否结束
            if self.flag>0: #有解，结束迭代
                break

单次迭代后对解的判断方法独立为Check()函数。
无可行解的情况出现在最后仍有人工变量非零，可在两阶段法的第一阶段确定。
特殊情况无界解的判定稍后分析。

    #Check()，检验是否为最优解且最优解是否唯一
    def Check(self):   	
        self.flag=1
        k=0
        for i in range(self.X_count):
            #检验数大于0，非最优解
            if self.C[i]>0:  
                self.flag=0
                break
            if abs(self.C[i])<0.00000001:   #计算存在误差
                k+=1
                #检验数中0的个数大于基变量个数，即存在非基变量检验数为零，则有无穷多最优解
                if k>self.b_count:
                    self.flag=2  

3.确定主元素，进行基变换

通过第二步我们计算出了所有的检验数。
找到最大检验数确定对应的换入变量。按照θ规则θi=min(bi/aik| aik>0) 确定换出变量。即能确定主元素。
在这里由于存在无界解这种特殊情况，该情况出现是因为在非基变量检验数大于0时theta无值可计算，非基变量系数小于零，即无约束。于是在FindMain()设计一个计数器，如果计数达到约束条件的行数，即theta全部为无穷大，设定special旗帜，则在最终输出时通过if可输出无界解的情形。

    def FindMain(self):