论文阅读笔记(16.append):附录详解:双重随机子空间聚类
参考我的上一篇博客,本文为对appendix部分的细读:
论文阅读笔记(16):Doubly Stochastic Subspace Clustering,双重随机子空间聚类
附录A: A-DSSC (序列近似双重随机子空间聚类)
A.1 A-DSSC对偶问题的梯度
回忆一下,在给定
C
C
C下求解
A
A
A的最优化问题,其中
A
∈
Ω
n
A\in\Omega_n
A∈Ωn是双随机凸集:

回忆一下A-DSSC的可伸缩有效集方法,通过计算 A ⊙ S A\odot S A⊙S使用只属于二值支撑集矩阵 S S S的 A A A对应元素
之后
α
,
β
\alpha, \beta
α,β的引入是用来表示凸集
Ω
n
\Omega_n
Ωn中对行和与列和为1的约束:
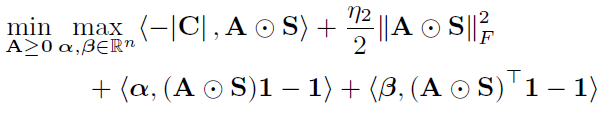
转化为了一个min-max问题,在把A看做不变量的情况下,找到能够最大化对行和( ( A ⊙ S ) 1 − 1 (A\odot S)1-1 (A⊙S)1−1)和列和( ( A ⊙ S ) ⊤ 1 − 1 (A\odot S)^\top1-1 (A⊙S)⊤1−1)约束的参数 α , β \alpha, \beta α,β,然后再求解最小化这样一个加了行列约束的目标函数的A
由于原始问题是凸的且具有严格可行点,Slater条件具有强对偶性,因此这等价于:
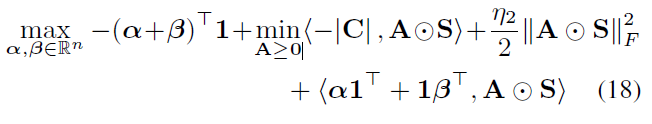
令
K
=
∣
C
∣
−
α
1
⊤
−
1
β
⊤
K=|C|-\alpha 1^\top -1\beta^\top
K=∣C∣−α1⊤−1β⊤:
那么上式(18)的minimize部分的第一项和第三项就可以合并为(19);
然后提取 η 2 \eta_2 η2得到(20);
由于 K K K与 A A A无关所以可以提到min外面得到(21)
[ K ] − [K]_- [K]−表示对其元素取 m i n { K , 0 } min\{K,0\} min{K,0},整流掉正部分
这时我们再把 K = ∣ C ∣ − α 1 ⊤ − 1 β ⊤ K=|C|-\alpha 1^\top -1\beta^\top K=∣C∣−α1⊤−1β⊤展开回代到(18)就得到了正文部分的对偶函数形式:
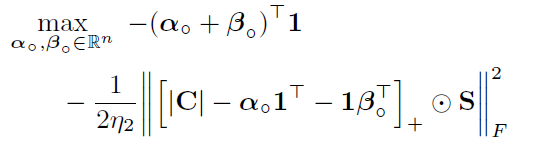
最佳解
A
A
A的值:
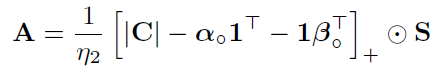
由公式(21)可看出来,对A的minimize部分就是一个二次回归问题,最佳的A应当有: A = A ∘ ⊙ S = 1 η 2 K ⊙ S A=A_\circ\odot S=\frac{1}{\eta_2}K\odot S A=A∘⊙S=η21K⊙S。没看懂可以回正文看算法2
A.2 有效集方法
这里,我们证明了算法2中的主动集方法在有限多个步骤内收敛到最优解。我们从一个引理开始:
引理 1
令 S S S的支撑集中包含了双随机非零模式,并有 ( α ∘ , β ∘ ) (\alpha_\circ, \beta_\circ) (α∘,β∘)为受限支撑集的对偶问题的解,那么如A.1附录所述: A ∘ = 1 η 2 [ ∣ C ∣ − α ∘ 1 ⊤ − 1 β ∘ ⊤ ] A_\circ = \frac{1}{\eta_2}[|C|-\alpha_\circ 1^\top -1\beta_\circ^\top] A∘=η21[∣C∣−α∘1⊤−1β∘⊤]在当且仅当 A ∘ A_\circ A∘是双重随机时,是原问题(具有不受限支撑集的)的最优解。
证明
很明显,任何最优解都是双重随机的,因为这是可行性条件。反过来说,假如
A
∘
A_\circ
A∘ 是双重随机的。注意,受限支撑集双重目标的次梯度由下式给出:
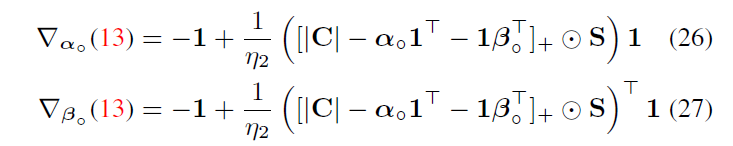
这里公式13指:
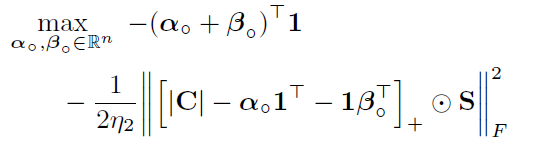
在不受限支撑集(即全支撑集)的情况下,次梯度精确测量
A
∘
A_\circ
A∘的行和列和偏离向量
1
\bf 1
1的程度。由于
A
∘
A_\circ
A∘是双重随机的,因此行与列的和都为1,自然次梯度为零。因此,
α
∘
α_\circ
α∘和
β
∘
β_\circ
β∘对于不受限支撑的对偶形式是最优的,这意味着我们可以将最优原始变量恢复为
1
η
2
[
∣
C
∣
−
α
∘
1
⊤
−
1
β
∘
⊤
]
\frac{1}{\eta_2}[|C|-\alpha_\circ 1^\top -1\beta_\circ^\top]
η21[∣C∣−α∘1⊤−1β∘⊤],这也就是
A
∘
A_\circ
A∘。
利用这一结果,我们可以直接得到对收敛性和正确性的证明:
命题 2
算法2中的
A
A
A可以在有限步内得到准确结果。
证明
注意到对
S
S
S的初始化给出了一个可行问题。因为支撑集包含一个双重随机的置换(permutation)矩阵。在每次迭代中,我们计算矩阵
A
∘
=
1
η
2
[
∣
C
∣
−
α
∘
1
⊤
−
1
β
∘
⊤
]
A_\circ=\frac{1}{\eta_2}[|C|-\alpha_\circ 1^\top -1\beta_\circ^\top]
A∘=η21[∣C∣−α∘1⊤−1β∘⊤]。若
A
∘
A_\circ
A∘是双重随机的,那么正如在引理1所证明的那样,这个在不受限支撑集问题中得到的
A
∘
A_\circ
A∘是最优的;若
A
∘
A_\circ
A∘不是双重随机的,那么
A
∘
≠
A
∘
⊙
S
A_\circ\neq A_\circ\odot S
A∘=A∘⊙S(因为
A
∘
⊙
S
A_\circ\odot S
A∘⊙S是双重随机的)。因此,支撑集被更新为以前从未见过的新支撑集,严格地说是更大的支撑集。只有有限多个支撑集,所以这个过程只有有限多个迭代,从而证明了我们算法的有限收敛性。
A.3 支撑集初始化
原始的(12)对于具有过多零元素的支撑集
S
S
S的某些选择可能不可行,因为不总是存在具有给定零-非零模式的双随机矩阵。我们希望对支撑集有一个初始化,该初始化既可行,能使我们的算法收敛,又更接近地包含最优
A
A
A的真实支撑集,因此收敛速度快。支撑集
A
A
A的一个合理猜测是每行的前
k
k
k个条目,因为这些条目对目标的内积贡献更大。此外,对于线性分配问题,即限制
η
2
=
0
η_2=0
η2=0的情况,每行的前k个条目已显示为包含高概率解
A
A
A的支撑集。但是,对于大小合理的k,不能保证top-k图是可行的,如下引理所示。
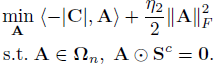
这是公式12
引理 2
令 n n n和 k k k为整数且有 n ≥ k ≥ 3 n\geq k\geq 3 n≥k≥3,
- 若 k < n / 2 k< n/2 k<n/2,那么在 n n n个节点上存在一个最小度为 k k k的图 G G G,使得 G G G的支撑集中不包含具有双随机矩阵的支撑集。
- 若 k ≥ n / 2 k\geq n/2 k≥n/2,那么在 n n n个节点上的任意图的支撑集中都存在一个最小度为 k k k的双随机矩阵。
证明
在
k
<
n
/
2
k<n/2
k<n/2时,有
n
−
k
>
n
/
2
>
k
n-k>n/2>k
n−k>n/2>k,考虑如下邻接矩阵图:
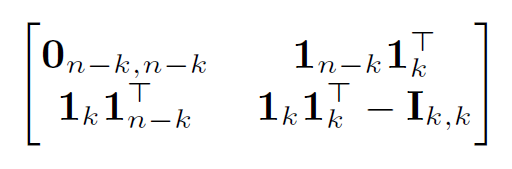
每一行具有
k
k
k个或
n
−
1
n-1
n−1个1,所以每个节点的度不少于
k
k
k。然而,在这个图的支撑集中不包含置换矩阵的支撑集。这是因为前
n
−
k
n−k
n−k个节点只有
k
k
k个独一无二的邻居,并有
n
−
k
>
k
n− k>k
n−k>k。
现在, k ≥ n / 2 k≥ n/2 k≥n/2,设 G G G是 n n n个节点上最小度为 k ≥ n / 2 k≥ n/2 k≥n/2的图。在具有至少 m m m个节点的连通分量的图中,最小度至少为 n / 2 ≥ m / 2 n/2≥ m/2 n/2≥m/2。因此,哈密顿圈的定理指出,每个连接的分量都有一个哈密顿循环(Hamiltonian cycle)——一个访问分量中每个节点的循环。取这些循环的和作为置换矩阵,我们得到了一个包含在这个图的支撑集的置换矩阵,因为置换矩阵是双重随机的。
为某些 k ≥ n / 2 k≥ n/2 k≥n/2选择top-k支撑集初始化违背了有效集方法的目的,因为在该支撑集中的求解仍然需要每个迭代进行 O ( n 2 ) \mathcal O(n^2) O(n2)复杂度的计算。在实践中,我们选择了一个小的 k k k,这导致了一个可处理的问题大小,并添加了一些随机抽样的排列矩阵来保证支撑集的可行性。
A.4 自表示的计算
对于受限支撑集 S S S的一般对偶问题(13),我们只需要计算 ( i , j ) ∈ s u p p ( S ) (i,j)∈supp(S) (i,j)∈supp(S)的 C i j C_{ij} Cij。如果内存不足是一个问题,那么这些 C i j C_{ij} Cij可以在每次迭代中在线计算,或者可以预计算并以 O ( ∣ S ∣ ) \mathcal O(|S|) O(∣S∣)的空间复杂度存储,以更快地进行目标和次梯度的计算。
特别是,通过计算稠密LSR解
C
C
C的子集,或在线计算,我们可以将LSR扩展到更大的数据集,如MNIST和EMNIST。在这些数据集中无法存储整个密集的
n
×
n
n×n
n×n的
C
C
C。要了解这是如何实现的,请注意,参数为
γ
γ
γ且没有零对角约束的LSR解(即
η
1
=
γ
,
η
3
=
0
η_1=γ,η_3=0
η1=γ,η3=0的解)可以如下表示:
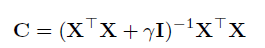
伍德伯里矩阵恒等式将该矩阵化为:

其中我们可以通过 C i j = X i ⊤ M X j C_{ij}=X^\top_iMX_j Cij=Xi⊤MXj计算。注意到M矩阵是 d × d d\times d d×d的,在这种计算中,我们不需要生成 n × n n×n n×n的矩阵。
附录B: J-DSSC (联合学习双重随机子空间聚类)
B.1 线性ADMM算法求解J-DSSC
我们通过引入附加变量 Y = A Y=A Y=A和 Z = X [ C p − C q ] Z=X[Cp−Cq] Z=X[Cp−Cq]来重参数化。这给了我们一个等价的优化目标:

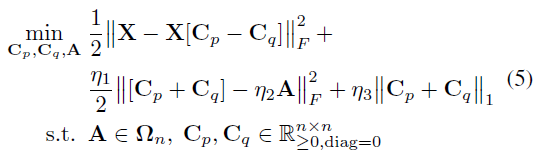
原问题的优化目标长这样,相当于把 Ω n \Omega_n Ωn的三个条件拆开来了,如前所述, C p − C q C_p-C_q Cp−Cq用来近似 C C C, C p + C q C_p+C_q Cp+Cq用来近似 ∣ C ∣ |C| ∣C∣
那么增广拉格朗日函数则变成了以下形式:

其中
I
S
\mathcal I_S
IS对应集合
S
S
S的指示函数:当在集合
S
S
S内时为0;当在集合外时为
∞
\infty
∞。在每次迭代中,我们在
C
p
C_p
Cp和
C
q
C_q
Cq中采用线性化的ADMM步骤,然后交替地在A、Y和Z上最小化,最后在每个拉格朗日乘子上采用梯度上升步骤。对于步长
τ
>
0
τ>0
τ>0,
C
p
C_p
Cp上的线性化ADMM步长采用梯度下降步长的形式:
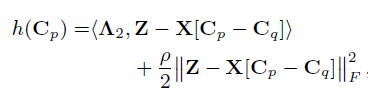
然后应用近端操作器。
C
p
′
C'_p
Cp′为梯度下降步骤后
C
p
C_p
Cp的中间值,Cp更新为以下的解:
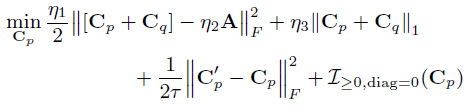
对于矩阵
E
E
E,
[
E
]
+
[E]_+
[E]+为
E
E
E的半波整流,
E
]
+
,
d
=
0
E]_{+,d=0}
E]+,d=0表示矩阵
E
E
E中所有负项和对角值均被置零。然后,线性化的ADMM更新如下所示:

A、Y、Z上按顺序最小化,保持其他变量不变,并使用每个变量的最新值,其形式如下:

拉格朗日乘子上的对偶上升步骤采用以下形式:
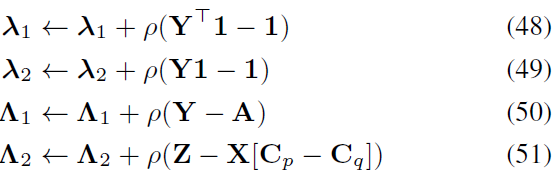
最后看一下用上面公式得到的J-DSSC算法:























 702
702











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








