插值算法以及在matlab中的应用

概念

插值：在数模的题目中，常常会有已知点的数量过少而不支持现有分析的情况，此时我们经常使用插值的方法来‘模拟’出比较靠谱的数据，以支撑我们的分析（插值的结果所得函数必须要经过已知点）

数学理论

插值法的概念

• 若所得的插值函数P（x）为分段多项式，则称为是分段插值
• 若所得的插值函数P（x）为三角多项式，则称为是三角插值（三角插值一般要用到傅里叶变换等复杂数学工具）

插值法定理

设有n+1个互不相同的节点（Xi，Yi）（i=0，1，…n），则存在唯一的n次多项式使得插值法能够成立（证明略）
这个定理告诉了我们插值函数是一定存在的

龙格现象（Rung phenomenon）

有时候为了提高插值函数的精度，我们会提高插值函数的次数，但是高次插值会产生龙格现象，即在两端波动极大，会产生明显的震荡，所以在平时插值时，在不熟悉曲线的运动趋势下，不要轻易使用插值函数

几种插值方法

分段线性插值

采用分段低次插值的方法，能减少龙格现象带来的影响，也能解决随着次数提高插值函数精度未显著提高的问题

---

分段二次插值

在几何上理解就是用分段抛物线来代替f(x)，所以又称为抛物线插值

---

埃尔米特（Hermite）插值

[y]=pchip（x，y，New_x）;
[y]中包含应变量的值

三次样条插值

[y]=spline(x,y,New_x);
[y]中包含应变量的值

上面这两中插值在实际应用中使用较多，实践性强，所以理论部分略过

---

建模实例

• 题目
  
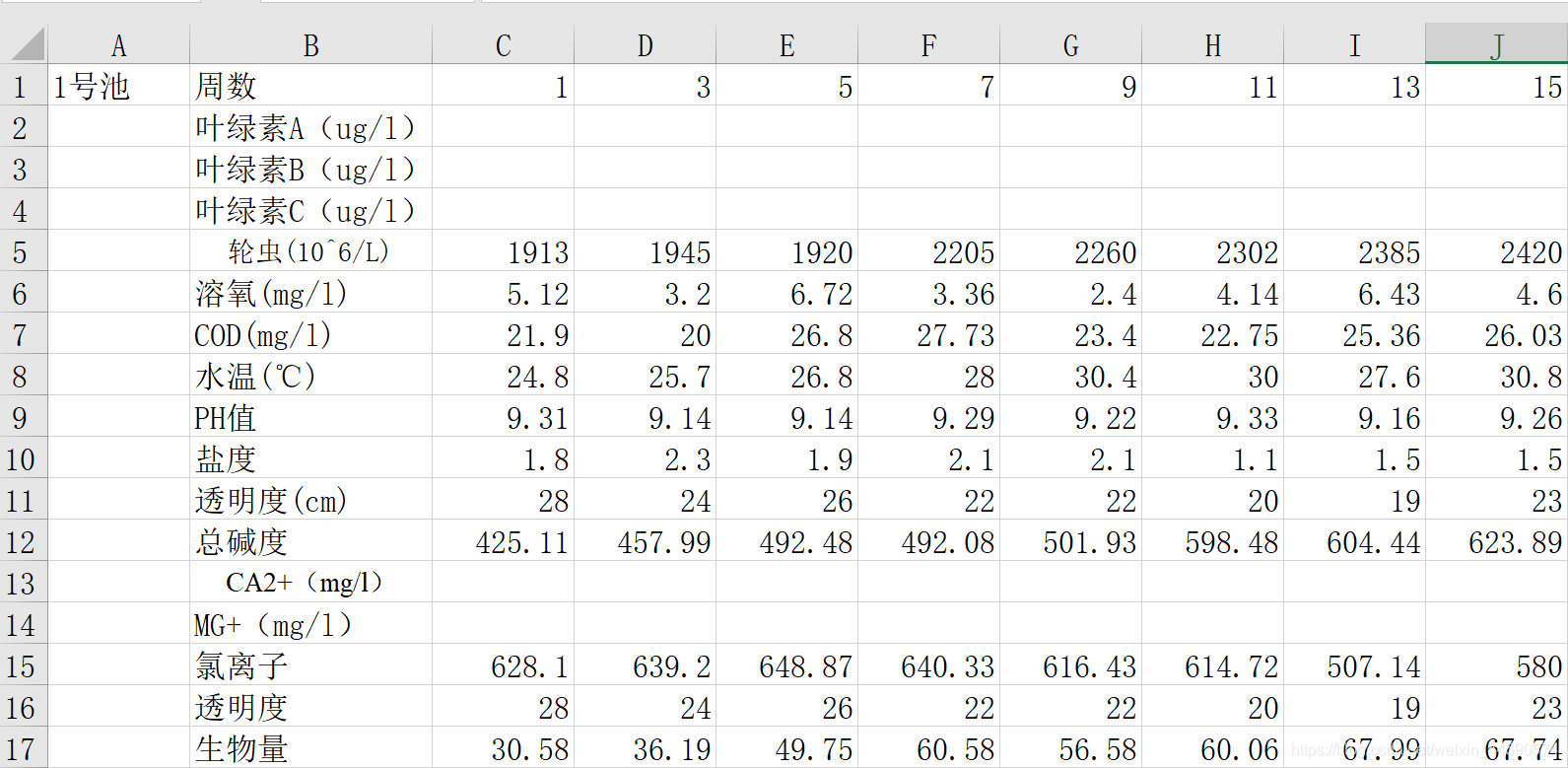
  表中所给的是奇数周数据，通过插值来预测1-15周所有周的数据
• 代码

clear all;clc;
load data.mat%数据已经预先存储在data文件中
x=[1:2:15];%已知点的横坐标
X=[1:15];%待插值的点
ylab={'周数','轮虫','溶氧','COD','水温','PH值','盐度','透明度','总碱度','氯离子','透明度','生物量'};
Y=spline([1:2:15],data,X);%返回待插值点的纵坐标
for i=1:11
    subplot(4,3,i);
    plot(x,data(i,:),'ro',X,Y(i,:),'-');
    axis([0 15 -inf inf]);%设置横纵坐标范围
    ylabel(ylab{i});%y轴的标签，直接引用元胞数组中的字符串

end
legend('原始数据','三次样条插值数据','location','SouthEast')

• 运行结果
  

• 注：在实际的比赛中，一般不会用插值来进行预测，拟合以及其他预测方法会用的多一些