编译原理: 最小化 DFA(划分) & 验证 DFA(Kleene 闭包)
文章目录
简介
作为正则表达式转 DFA 三部曲的最后一部,本篇将解说四个步骤:
- Thompson 构造法:正则表达式 RegExp -> 不确定有限状态机 NFA
- 子集构造法:不确定有限状态机 NFA -> 确定有限状态机 DFA
- 最小化:最小化确定有限状态机 DFA
- 验证:DFA 转换为的等价正则表达式并验证等价
中的最后两步:最小化和验证
参考
| 编译原理-DFA与正规式的转化 | https://www.cnblogs.com/mznsndy/p/10742827.html |
正文
示例回顾
我们在前两部使用了两个例子作为范例,完成了从正则表达式 -> NFA -> DFA 的转换,最终结果是一张 DFA 图:
示例1: a ( b ∣ c ) ∗ a(b|c)^{*} a(b∣c)∗


示例2: ( a ∣ b ) ∗ a b b (a|b)^{*}abb (a∣b)∗abb

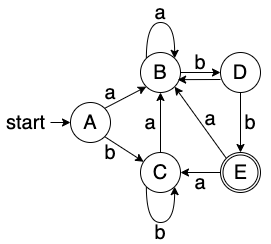
然而这样构建出来的 DFA 其实还存在相当大的冗余部分,接下来我们就要透过Kleene 闭包来最小化 DFA,同时验证简化后的 DFA 和原来的正则表达式是等价的。
最小化 DFA(划分)
怎么划分?
直接上伪代码
Min-DFA(Dtran)
let U = {S\F, F} # 初始的等价类有两个组,分别是非终止状态和终止状态
for (G in U) { # 对等价类中每个组做划分
while (G can be divided) {
g1, g2, g3, ... = divide(G)
remove G from U
add g1, g2, g3, ... into U
}
}
- 首先将上面的 DFA 分为非终止状态和终止状态两组,然后对每一组进行检查是否能够再做划分,若可则对划分后的组再划分,直到不可再划分
- 最后根据划分后的组重建 Dtran 表并重绘 DFA 图
-
这边需要说明一下
不可划分的概念:若对于组内所有状态,对于所有输入都有相同的输出状态,则称该组
不可再被划分。
其实简单的看就是当 Dtran 右侧的转移函数的行相同时就可以被分为一组
最小化示例
示例1: a ( b ∣ c ) ∗ a(b|c)^{*} a(b∣c)∗

首先根据是否为终止状态(是否包含 a10)划分为两组: U = { { A } , { B , C , D } } U = \{\{A\},\{B,C,D\}\} U={{A},{B,C,D}}
接下来我们发现对于组 B , C , D {B,C,D} B,C,D 中的每一个状态,对于同一个输入都有同样的输出状态( D t r a n [ X , b ] = C , D t r a n [ X , c ] = D Dtran[X,b]=C, Dtran[X,c]=D Dtran[X,b]=C,Dtran[X,c]=D),则组 B , C , D {B,C,D} B,C,D 不可再被划分了,因此最终划分便是 U = { { A } , { B , C , D } } U = \{\{A\},\{B,C,D\}\} U={{A},{B,C,D}}
我们使用 B ′ B^{'} B′ 来取代原来 B , C , D B,C,D B,C,D 的位置并重建 D t r a n Dtran Dtran 跟 D F A DFA DFA
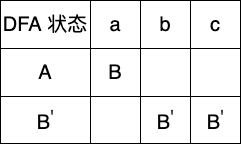

示例2: ( a ∣ b ) ∗ a b b (a|b)^{*}abb (a∣b)∗abb

初始划分为 U = { { A , B , C , D } , { E } } U = \{\{A,B,C,D\},\{E\}\} U={{A,B,C,D},{E}},然后我们发现只有 A , C A,C A,C 的转换函数结果完全相同( D t r a n [ A ∣ C , a ] = B , D t r a n [ A ∣ C , b ] = C Dtran[A|C,a]=B, Dtran[A|C,b]=C Dtran[A∣C,a]=B,Dtran[A∣C,b]=C),则我们使用 A ′ A^{'} A′ 来取代 A , C A,C A,C,最终划分为 U = { A ′ : { A , C } , { B } , { D } , { E } } U = \{A^{'}: \{A,C\},\{B\},\{D\},\{E\}\} U={A′:{A,C},{B},{D},{E}},新的 D t r a n Dtran Dtran 跟 D F A DFA DFA 如下
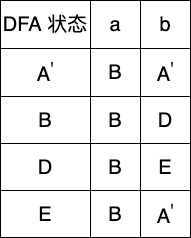
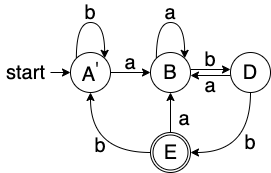
验证 DFA
接下来我们要验证我们最小化后的 DFA 与原来的正则表达式是等价的,我们将使用 Kleene 闭包来完成这个动作
Kleene 闭包定义 R i j k R_{ij}^{k} Rijk
-
符号定义: R i j k R_{ij}^{k} Rijk、 ⊘ \oslash ⊘、 ϵ \epsilon ϵ
-
R i j k R_{ij}^{k} Rijk 表示 Kleene 闭包
我们将 DFA 中所有节点依序编号为为 0 ∼ n − 1 0 \sim n - 1 0∼n−1
R i j k R_{ij}^{k} Rijk 则表示从节点 i i i 到节点 j j j 途中经过小于等于编号为 k k k 的中间节点可达的所有路径
-
⊘ \oslash ⊘ 表示路径不可达
对于路径不可达的并( ∣ | ∣和)连接( ∩ \cap ∩)操作有以下结果:- 并: ⊘ ∣ a = a \oslash | a = a ⊘∣a=a
- 连接: ⊘ a = ⊘ \oslash a = \oslash ⊘a=⊘
注意:不可达 ⊘ \oslash ⊘ 与空串 ϵ \epsilon ϵ 不同
- ϵ ∣ a = a \epsilon | a = a ϵ∣a=a
- ϵ a = a \epsilon a = a ϵa=a
-
ϵ \epsilon ϵ 表示空路径,即状态不发生变化的边(回到同一状态)
-
-
Kleene 初始化 k = − 1 k = -1 k=−1
而接下来我们介绍 Kleene 闭包的
初始化状态R i j − 1 R_{ij}^{-1} Rij−1 表示从节点 i i i 到节点 j j j 不经过
任意节点的所有路径以下为初始化状态的示例
R i j − 1 = a ∣ b ∣ c R_{ij}^{-1} = a|b|c Rij−1=a∣b∣c
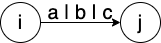
R i j − 1 = ⊘ R_{ij}^{-1} = \oslash Rij−1=⊘

R i i − 1 = a ∣ ϵ R_{ii}^{-1} = a|\epsilon Rii−1=a∣ϵ

R i i − 1 = ϵ R_{ii}^{-1} = \epsilon Rii−1=ϵ

我们可以看到当出节点和入节点相同时( i = j i = j i=j),路径中必然存在一个 ϵ \epsilon ϵ
-
Kleene 递归步
k = − 1 k = -1 k=−1时表示不经过任何中间节点,接下来我们就慢慢的让中间节点的编号限制( k k k)慢慢向上累加,核心公式如下:
R i j k = R i k k − 1 ( R k k k − 1 ) ∗ R k j k − 1 ∣ R i j k − 1 R_{ij}^{k} = R_{ik}^{k-1}(R_{kk}^{k-1})^{\ast}R_{kj}^{k-1}|R_{ij}^{k-1} Rijk=Rikk−1(Rkkk−1)∗Rkjk−1∣Rijk−1
这个转换式的意思就是新的经过 k k k 以下的中间节点的结果就是旧的路径经过 k − 1 k-1 k−1 的中间节点与原路径的并,如下图所示
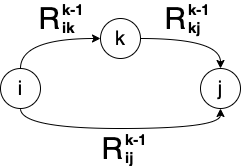
有了 Kleene 闭包,我们就可以来找 s s s(起始节点)到 t t t 终止节点
重建 RE 并验证等价
接下来所谓的重建其实就是透过 Kleene 闭包来重建正则表达式,也就是说我们要找的目标就是 R i j k , i = s 0 , j = f , k = S R_{ij}^{k}, i=s0, j=f, k=S Rijk,i=s0,j=f,k=S,我们透过不断增加 k k k 值来找到我们的最终结果,接下来直接使用示例来解说吧(在此我们先将示例的状态重新编号)
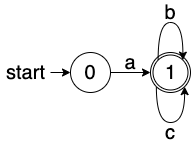
示例1: a ( b ∣ c ) ∗ a(b|c)^{*} a(b∣c)∗
-
初始化状态: k = − 1 k = -1 k=−1
R 00 − 1 = ϵ R_{00}^{-1} = \epsilon R00−1=ϵ
R 01 − 1 = a R_{01}^{-1} = a R01−1=a
R 10 − 1 = ⊘ R_{10}^{-1} = \oslash R10−1=⊘
R 11 − 1 = b ∣ c ∣ ϵ R_{11}^{-1} = b|c|\epsilon R11−1=b∣c∣ϵ -
k = 0 k = 0 k=0
R 00 0 = R 00 − 1 ( R 00 − 1 ) ∗ R 00 − 1 ∣ R 00 − 1 = ϵ ( ϵ ) ∗ ϵ = ϵ R_{00}^{0} = R_{00}^{-1} (R_{00}^{-1})^{\ast} R_{00}^{-1} | R_{00}^{-1} = \epsilon (\epsilon)^{\ast} \epsilon = \epsilon R000=R00−1(R00−1)∗R00−1∣R00−1=ϵ(ϵ)∗ϵ=ϵ
R 01 0 = R 00 − 1 ( R 00 − 1 ) ∗ R 01 − 1 ∣ R 01 − 1 = ϵ ( ϵ ) ∗ a = a R_{01}^{0} = R_{00}^{-1} (R_{00}^{-1})^{\ast} R_{01}^{-1} | R_{01}^{-1} = \epsilon (\epsilon)^{\ast} a = a R010=R00−1(R00−1)∗R01−1∣R01−1=ϵ(ϵ)∗a=a
R 10 0 = R 10 − 1 ( R 00 − 1 ) ∗ R 00 − 1 ∣ R 10 − 1 = ⊘ ( ϵ ) ∗ ⊘ = ⊘ R_{10}^{0} = R_{10}^{-1} (R_{00}^{-1})^{\ast} R_{00}^{-1} | R_{10}^{-1} = \oslash (\epsilon)^{\ast} \oslash = \oslash R100=R10−1(R00−1)∗R00−1∣R10−1=⊘(ϵ)∗⊘=⊘
R 11 0 = R 10 − 1 ( R 00 − 1 ) ∗ R 01 − 1 ∣ R 11 − 1 = ⊘ ( ϵ ) ∗ ( b ∣ c ∣ ϵ ) = b ∣ c ∣ ϵ R_{11}^{0} = R_{10}^{-1} (R_{00}^{-1})^{\ast} R_{01}^{-1} | R_{11}^{-1} = \oslash (\epsilon)^{\ast} (b|c|\epsilon) = b|c|\epsilon R110=R10−1(R00−1)∗R01−1∣R11−1=⊘(ϵ)∗(b∣c∣ϵ)=b∣c∣ϵ -
k = 1 k = 1 k=1
R 00 1 = R 01 0 ( R 11 0 ) ∗ R 00 0 ∣ R 10 0 = a ( b ∣ c ∣ ϵ ) ∗ ⊘ ∣ ϵ = ϵ R_{00}^{1} = R_{01}^{0} (R_{11}^{0})^{\ast} R_{00}^{0} | R_{10}^{0} = a (b|c|\epsilon)^{\ast} \oslash|\epsilon = \epsilon R001=R010(R110)∗R000∣R100=a(b∣c∣ϵ)∗⊘∣ϵ=ϵ
R 01 1 = R 01 0 ( R 11 0 ) ∗ R 01 0 ∣ R 11 0 = a ( b ∣ c ∣ ϵ ) ∗ ( b ∣ c ∣ ϵ ) ∣ a = a ( b ∣ c ) ∗ R_{01}^{1} = R_{01}^{0} (R_{11}^{0})^{\ast} R_{01}^{0} | R_{11}^{0} = a (b|c|\epsilon)^{\ast} (b|c|\epsilon)|a = a(b|c)^{\ast} R011=R010(R110)∗R010∣R110=a(b∣c∣ϵ)∗(b∣c∣ϵ)∣a=a(b∣c)∗
R 10 1 = R 11 0 ( R 11 0 ) ∗ R 00 0 ∣ R 10 0 = ( b ∣ c ∣ ϵ ) ( b ∣ c ∣ ϵ ) ∗ ⊘ ∣ ⊘ = ⊘ R_{10}^{1} = R_{11}^{0} (R_{11}^{0})^{\ast} R_{00}^{0} | R_{10}^{0} = (b|c|\epsilon) (b|c|\epsilon)^{\ast} \oslash|\oslash = \oslash R101=R110(R110)∗R000∣R100=(b∣c∣ϵ)(b∣c∣ϵ)∗⊘∣⊘=⊘
R 11 1 = R 11 0 ( R 11 0 ) ∗ R 01 0 ∣ R 11 0 = ( b ∣ c ∣ ϵ ) ( b ∣ c ∣ ϵ ) ∗ ( b ∣ c ∣ ϵ ) ∣ ( b ∣ c ∣ ϵ ) = ( b ∣ c ) ∗ R_{11}^{1} = R_{11}^{0} (R_{11}^{0})^{\ast} R_{01}^{0} | R_{11}^{0} = (b|c|\epsilon) (b|c|\epsilon)^{\ast} (b|c|\epsilon)|(b|c|\epsilon) = (b|c)^{\ast} R111=R110(R110)∗R010∣R110=(b∣c∣ϵ)(b∣c∣ϵ)∗(b∣c∣ϵ)∣(b∣c∣ϵ)=(b∣c)∗
最后我们使用 Kleene 闭包重建出来的正则表达式 R 01 1 = a ( b ∣ c ) ∗ R_{01}^{1} = a(b|c)^{\ast} R011=a(b∣c)∗ 与原表达式相同,证明新的 DFA 与原正则表达式为等价。
示例2: ( a ∣ b ) ∗ a b b (a|b)^{*}abb (a∣b)∗abb

-
初始化状态: k = − 1 k = -1 k=−1
R 00 − 1 = b ∣ ϵ R_{00}^{-1} = b|\epsilon R00−1=b∣ϵ
R 01 − 1 = a R_{01}^{-1} = a R01−1=a
R 02 − 1 = ⊘ R_{02}^{-1} = \oslash R02−1=⊘
R 03 − 1 = ⊘ R_{03}^{-1} = \oslash R03−1=⊘
R 10 − 1 = ⊘ R_{10}^{-1} = \oslash R10−1=⊘
R 11 − 1 = a ∣ ϵ R_{11}^{-1} = a|\epsilon R11−1=a∣ϵ
R 12 − 1 = b R_{12}^{-1} = b R12−1=b
R 13 − 1 = ⊘ R_{13}^{-1} = \oslash R13−1=⊘
R 20 − 1 = ⊘ R_{20}^{-1} = \oslash R20−1=⊘
R 21 − 1 = a R_{21}^{-1} = a R21−1=a
R 22 − 1 = ϵ R_{22}^{-1} = \epsilon R22−1=ϵ
R 23 − 1 = b R_{23}^{-1} = b R23−1=b
R 30 − 1 = b R_{30}^{-1} = b R30−1=b
R 31 − 1 = a R_{31}^{-1} = a R31−1=a
R 32 − 1 = ⊘ R_{32}^{-1} = \oslash R32−1=⊘
R 33 − 1 = ϵ R_{33}^{-1} = \epsilon R33−1=ϵ -
k = 0 k = 0 k=0
R 00 0 = R 00 − 1 ( R 00 − 1 ) ∗ R 00 − 1 ∣ R 00 − 1 = ( b ∣ ϵ ) ( b ∣ ϵ ) ∗ ( b ∣ ϵ ) ∣ ( b ∣ ϵ ) = b ∗ R_{00}^{0} = R_{00}^{-1} (R_{00}^{-1})^{\ast} R_{00}^{-1} | R_{00}^{-1} = (b|\epsilon) (b|\epsilon)^{\ast} (b|\epsilon) | (b|\epsilon) = b^{\ast} R000=R00−1(R00−1)∗R00−1∣R00−1=(b∣ϵ)(b∣ϵ)∗(b∣ϵ)∣(b∣ϵ)=b∗
R 01 0 = R 00 − 1 ( R 00 − 1 ) ∗ R 01 − 1 ∣ R 01 − 1 = ( b ∣ ϵ ) ( b ∣ ϵ ) ∗ a ∣ a = b ∗ a R_{01}^{0} = R_{00}^{-1} (R_{00}^{-1})^{\ast} R_{01}^{-1} | R_{01}^{-1} = (b|\epsilon) (b|\epsilon)^{\ast} a | a = b^{\ast}a R010=R00−1(R00−1)∗R01−1∣R01−1=(b∣ϵ)(b∣ϵ)∗a∣a=b∗a
R 02 0 = R 00 − 1 ( R 00 − 1 ) ∗ R 02 − 1 ∣ R 02 − 1 = ( b ∣ ϵ ) ( b ∣ ϵ ) ∗ ⊘ ∣ ⊘ = ⊘ R_{02}^{0} = R_{00}^{-1} (R_{00}^{-1})^{\ast} R_{02}^{-1} | R_{02}^{-1} = (b|\epsilon) (b|\epsilon)^{\ast} \oslash | \oslash = \oslash R020=R00−1(R00−1)∗R02−1∣R02−1=(b∣ϵ)(b∣ϵ)∗⊘∣⊘=⊘
R 03 0 = R 00 − 1 ( R 00 − 1 ) ∗ R 03 − 1 ∣ R 03 − 1 = ( b ∣ ϵ ) ( b ∣ ϵ ) ∗ ⊘ ∣ ⊘ = ⊘ R_{03}^{0} = R_{00}^{-1} (R_{00}^{-1})^{\ast} R_{03}^{-1} | R_{03}^{-1} = (b|\epsilon) (b|\epsilon)^{\ast} \oslash | \oslash = \oslash R030=R00−1(R00−1)∗R03−1∣R03−1=(b∣ϵ)(b∣ϵ)∗⊘∣⊘=⊘
R 10 0 = R 10 − 1 ( R 00 − 1 ) ∗ R 00 − 1 ∣ R 10 − 1 = ⊘ ( b ∣ ϵ ) ∗ ( b ∣ ϵ ) ∣ ⊘ = ⊘ R_{10}^{0} = R_{10}^{-1} (R_{00}^{-1})^{\ast} R_{00}^{-1} | R_{10}^{-1} = \oslash (b|\epsilon)^{\ast} (b|\epsilon) | \oslash = \oslash R100=R10−1(R00−1)∗R00−1∣R10−1=⊘(b∣ϵ)∗(b∣ϵ)∣⊘=⊘
R 11 0 = R 10 − 1 ( R 00 − 1 ) ∗ R 01 − 1 ∣ R 11 − 1 = ⊘ ( b ∣ ϵ ) ∗ a ∣ ( a ∣ ϵ ) = a ∣ ϵ R_{11}^{0} = R_{10}^{-1} (R_{00}^{-1})^{\ast} R_{01}^{-1} | R_{11}^{-1} = \oslash (b|\epsilon)^{\ast} a | (a|\epsilon) = a|\epsilon R110=R10−1(R00−1)∗R01−1∣R11−1=⊘(b∣ϵ)∗a∣(a∣ϵ)=a∣ϵ
R 12 0 = R 10 − 1 ( R 00 − 1 ) ∗ R 02 − 1 ∣ R 12 − 1 = ⊘ ( b ∣ ϵ ) ∗ ⊘ ∣ b = b R_{12}^{0} = R_{10}^{-1} (R_{00}^{-1})^{\ast} R_{02}^{-1} | R_{12}^{-1} = \oslash (b|\epsilon)^{\ast} \oslash | b = b R120=R10−1(R00−1)∗R02−1∣R12−1=⊘(b∣ϵ)∗⊘∣b=b
R 13 0 = R 10 − 1 ( R 00 − 1 ) ∗ R 03 − 1 ∣ R 13 − 1 = ⊘ ( b ∣ ϵ ) ∗ ⊘ ∣ ⊘ = ⊘ R_{13}^{0} = R_{10}^{-1} (R_{00}^{-1})^{\ast} R_{03}^{-1} | R_{13}^{-1} = \oslash (b|\epsilon)^{\ast} \oslash | \oslash = \oslash R130=R10−1(R00−1)∗R03−1∣R13−1=⊘(b∣ϵ)∗⊘∣⊘=⊘
R 20 0 = R 20 − 1 ( R 00 − 1 ) ∗ R 00 − 1 ∣ R 20 − 1 = ⊘ ( b ∣ ϵ ) ∗ ( b ∣ ϵ ) ∣ ⊘ = ⊘ R_{20}^{0} = R_{20}^{-1} (R_{00}^{-1})^{\ast} R_{00}^{-1} | R_{20}^{-1} = \oslash (b|\epsilon)^{\ast} (b|\epsilon) | \oslash = \oslash R200=R20−1(R00−1)∗R00−1∣R20−1=⊘(b∣ϵ)∗(b∣ϵ)∣⊘=⊘
R 21 0 = R 20 − 1 ( R 00 − 1 ) ∗ R 01 − 1 ∣ R 21 − 1 = ⊘ ( b ∣ ϵ ) ∗ a ∣ a = a R_{21}^{0} = R_{20}^{-1} (R_{00}^{-1})^{\ast} R_{01}^{-1} | R_{21}^{-1} = \oslash (b|\epsilon)^{\ast} a | a = a R210=R20−1(R00−1)∗R01−1∣R21−1=⊘(b∣ϵ)∗a∣a=a
R 22 0 = R 20 − 1 ( R 00 − 1 ) ∗ R 02 − 1 ∣ R 22 − 1 = ⊘ ( b ∣ ϵ ) ∗ ⊘ ∣ ϵ = ϵ R_{22}^{0} = R_{20}^{-1} (R_{00}^{-1})^{\ast} R_{02}^{-1} | R_{22}^{-1} = \oslash (b|\epsilon)^{\ast} \oslash | \epsilon = \epsilon R220=R20−1(R00−1)∗R02−1∣R22−1=⊘(b∣ϵ)∗⊘∣ϵ=ϵ
R 23 0 = R 20 − 1 ( R 00 − 1 ) ∗ R 03 − 1 ∣ R 23 − 1 = ⊘ ( b ∣ ϵ ) ∗ ⊘ ∣ b = b R_{23}^{0} = R_{20}^{-1} (R_{00}^{-1})^{\ast} R_{03}^{-1} | R_{23}^{-1} = \oslash (b|\epsilon)^{\ast} \oslash | b = b R230=R20−1(R00−1)∗R03−1∣R23−1=⊘(b∣ϵ)∗⊘∣b=b
R 30 0 = R 30 − 1 ( R 00 − 1 ) ∗ R 00 − 1 ∣ R 30 − 1 = b ( b ∣ ϵ ) ∗ ( b ∣ ϵ ) ∣ b = b ∗ R_{30}^{0} = R_{30}^{-1} (R_{00}^{-1})^{\ast} R_{00}^{-1} | R_{30}^{-1} = b (b|\epsilon)^{\ast} (b|\epsilon) | b = b^{\ast} R300=R30−1(R00−1)∗R00−1∣R30−1=b(b∣ϵ)∗(b∣ϵ)∣b=b∗
R 31 0 = R 30 − 1 ( R 00 − 1 ) ∗ R 01 − 1 ∣ R 31 − 1 = b ( b ∣ ϵ ) ∗ a ∣ a = b ∗ a R_{31}^{0} = R_{30}^{-1} (R_{00}^{-1})^{\ast} R_{01}^{-1} | R_{31}^{-1} = b (b|\epsilon)^{\ast} a | a = b^{\ast}a R310=R30−1(R00−1)∗R01−1∣R31−1=b(b∣ϵ)∗a∣a=b∗a
R 32 0 = R 30 − 1 ( R 00 − 1 ) ∗ R 02 − 1 ∣ R 32 − 1 = b ( b ∣ ϵ ) ∗ ⊘ ∣ ⊘ = ⊘ R_{32}^{0} = R_{30}^{-1} (R_{00}^{-1})^{\ast} R_{02}^{-1} | R_{32}^{-1} = b (b|\epsilon)^{\ast} \oslash | \oslash = \oslash R320=R30−1(R00−1)∗R02−1∣R32−1=b(b∣ϵ)∗⊘∣⊘=⊘
R 33 0 = R 30 − 1 ( R 00 − 1 ) ∗ R 03 − 1 ∣ R 33 − 1 = b ( b ∣ ϵ ) ∗ ⊘ ∣ ϵ = ϵ R_{33}^{0} = R_{30}^{-1} (R_{00}^{-1})^{\ast} R_{03}^{-1} | R_{33}^{-1} = b (b|\epsilon)^{\ast} \oslash | \epsilon = \epsilon R330=R30−1(R00−1)∗R03−1∣R33−1=b(b∣ϵ)∗⊘∣ϵ=ϵ -
k = 1 k = 1 k=1
R 00 1 = R 01 0 ( R 11 0 ) ∗ R 10 0 ∣ R 00 0 = ( b ∗ a ) ( a ∣ ϵ ) ∗ ⊘ ∣ b ∗ = b ∗ R_{00}^{1} = R_{01}^{0} (R_{11}^{0})^{\ast} R_{10}^{0} | R_{00}^{0} = (b^{\ast}a) (a|\epsilon)^{\ast} \oslash | b^{\ast} = b^{\ast} R001=R010(R110)∗R100∣R000=(b∗a)(a∣ϵ)∗⊘∣b∗=b∗
R 01 1 = R 01 0 ( R 11 0 ) ∗ R 11 0 ∣ R 01 0 = ( b ∗ a ) ( a ∣ ϵ ) ∗ ( a ∣ ϵ ) ∣ ( b ∗ a ) = b ∗ a + R_{01}^{1} = R_{01}^{0} (R_{11}^{0})^{\ast} R_{11}^{0} | R_{01}^{0} = (b^{\ast}a) (a|\epsilon)^{\ast} (a|\epsilon) | (b^{\ast}a) = b^{\ast}a^{+} R011=R010(R110)∗R110∣R010=(b∗a)(a∣ϵ)∗(a∣ϵ)∣(b∗a)=b∗a+
R 02 1 = R 01 0 ( R 11 0 ) ∗ R 12 0 ∣ R 02 0 = ( b ∗ a ) ( a ∣ ϵ ) ∗ b ∣ ⊘ = b ∗ a + b R_{02}^{1} = R_{01}^{0} (R_{11}^{0})^{\ast} R_{12}^{0} | R_{02}^{0} = (b^{\ast}a) (a|\epsilon)^{\ast} b | \oslash = b^{\ast}a^{+}b R021=R010(R110)∗R120∣R020=(b∗a)(a∣ϵ)∗b∣⊘=b∗a+b
R 03 1 = R 01 0 ( R 11 0 ) ∗ R 13 0 ∣ R 03 0 = ( b ∗ a ) ( a ∣ ϵ ) ∗ ⊘ ∣ ⊘ = ⊘ R_{03}^{1} = R_{01}^{0} (R_{11}^{0})^{\ast} R_{13}^{0} | R_{03}^{0} = (b^{\ast}a) (a|\epsilon)^{\ast} \oslash | \oslash = \oslash R031=R010(R110)∗R130∣R030=(b∗a)(a∣ϵ)∗⊘∣⊘=⊘
R 10 1 = R 11 0 ( R 11 0 ) ∗ R 10 0 ∣ R 10 0 = ( a ∣ ϵ ) ( a ∣ ϵ ) ∗ ⊘ ∣ ⊘ = ⊘ R_{10}^{1} = R_{11}^{0} (R_{11}^{0})^{\ast} R_{10}^{0} | R_{10}^{0} = (a|\epsilon) (a|\epsilon)^{\ast} \oslash | \oslash = \oslash R101=R110(R110)∗R100∣R100=(a∣ϵ)(a∣ϵ)∗⊘∣⊘=⊘
R 11 1 = R 11 0 ( R 11 0 ) ∗ R 11 0 ∣ R 11 0 = ( a ∣ ϵ ) ( a ∣ ϵ ) ∗ ( a ∣ ϵ ) ∣ ( a ∣ ϵ ) = a ∗ R_{11}^{1} = R_{11}^{0} (R_{11}^{0})^{\ast} R_{11}^{0} | R_{11}^{0} = (a|\epsilon) (a|\epsilon)^{\ast} (a|\epsilon) | (a|\epsilon) = a^{\ast} R111=R110(R110)∗R110∣R110=(a∣ϵ)(a∣ϵ)∗(a∣ϵ)∣(a∣ϵ)=a∗
R 12 1 = R 11 0 ( R 11 0 ) ∗ R 12 0 ∣ R 12 0 = ( a ∣ ϵ ) ( a ∣ ϵ ) ∗ b ∣ b = a ∗ b R_{12}^{1} = R_{11}^{0} (R_{11}^{0})^{\ast} R_{12}^{0} | R_{12}^{0} = (a|\epsilon) (a|\epsilon)^{\ast} b | b = a^{\ast}b R121=R110(R110)∗R120∣R120=(a∣ϵ)(a∣ϵ)∗b∣b=a∗b
R 13 1 = R 11 0 ( R 11 0 ) ∗ R 13 0 ∣ R 13 0 = ( a ∣ ϵ ) ( a ∣ ϵ ) ∗ ⊘ ∣ ⊘ = ⊘ R_{13}^{1} = R_{11}^{0} (R_{11}^{0})^{\ast} R_{13}^{0} | R_{13}^{0} = (a|\epsilon) (a|\epsilon)^{\ast} \oslash | \oslash = \oslash R131=R110(R110)∗R130∣R130=(a∣ϵ)(a∣ϵ)∗⊘∣⊘=⊘
R 20 1 = R 21 0 ( R 11 0 ) ∗ R 10 0 ∣ R 20 0 = a ( a ∣ ϵ ) ∗ ⊘ ∣ ⊘ = ⊘ R_{20}^{1} = R_{21}^{0} (R_{11}^{0})^{\ast} R_{10}^{0} | R_{20}^{0} = a (a|\epsilon)^{\ast} \oslash | \oslash = \oslash R201=R210(R110)∗R100∣R200=a(a∣ϵ)∗⊘∣⊘=⊘
R 21 1 = R 21 0 ( R 11 0 ) ∗ R 11 0 ∣ R 21 0 = a ( a ∣ ϵ ) ∗ ( a ∣ ϵ ) ∣ a = a + R_{21}^{1} = R_{21}^{0} (R_{11}^{0})^{\ast} R_{11}^{0} | R_{21}^{0} = a (a|\epsilon)^{\ast} (a|\epsilon) | a = a^{+} R211=R210(R110)∗R110∣R210=a(a∣ϵ)∗(a∣ϵ)∣a=a+
R 22 1 = R 21 0 ( R 11 0 ) ∗ R 12 0 ∣ R 22 0 = a ( a ∣ ϵ ) ∗ b ∣ ϵ = a + b ∣ ϵ R_{22}^{1} = R_{21}^{0} (R_{11}^{0})^{\ast} R_{12}^{0} | R_{22}^{0} = a (a|\epsilon)^{\ast} b | \epsilon = a^{+}b|\epsilon R221=R210(R110)∗R120∣R220=a(a∣ϵ)∗b∣ϵ=a+b∣ϵ
R 23 1 = R 21 0 ( R 11 0 ) ∗ R 13 0 ∣ R 23 0 = a ( a ∣ ϵ ) ∗ ⊘ ∣ b = b R_{23}^{1} = R_{21}^{0} (R_{11}^{0})^{\ast} R_{13}^{0} | R_{23}^{0} = a (a|\epsilon)^{\ast} \oslash | b = b R231=R210(R110)∗R130∣R230=a(a∣ϵ)∗⊘∣b=b
R 30 1 = R 31 0 ( R 11 0 ) ∗ R 10 0 ∣ R 30 0 = ( b ∗ a ) ( a ∣ ϵ ) ∗ ⊘ ∣ b ∗ = b ∗ R_{30}^{1} = R_{31}^{0} (R_{11}^{0})^{\ast} R_{10}^{0} | R_{30}^{0} = (b^{\ast}a) (a|\epsilon)^{\ast} \oslash | b^{\ast} = b^{\ast} R301=R310(R110)∗R100∣R300=(b∗a)(a∣ϵ)∗⊘∣b∗=b∗
R 31 1 = R 31 0 ( R 11 0 ) ∗ R 11 0 ∣ R 31 0 = ( b ∗ a ) ( a ∣ ϵ ) ∗ ( a ∣ ϵ ) ∣ ( b ∗ a ) = b ∗ a + R_{31}^{1} = R_{31}^{0} (R_{11}^{0})^{\ast} R_{11}^{0} | R_{31}^{0} = (b^{\ast}a) (a|\epsilon)^{\ast} (a|\epsilon) | (b^{\ast}a) = b^{\ast}a^{+} R311=R310(R110)∗R110∣R310=(b∗a)(a∣ϵ)∗(a∣ϵ)∣(b∗a)=b∗a+
R 32 1 = R 31 0 ( R 11 0 ) ∗ R 12 0 ∣ R 32 0 = ( b ∗ a ) ( a ∣ ϵ ) ∗ b ∣ ⊘ = b ∗ a + b R_{32}^{1} = R_{31}^{0} (R_{11}^{0})^{\ast} R_{12}^{0} | R_{32}^{0} = (b^{\ast}a) (a|\epsilon)^{\ast} b | \oslash = b^{\ast}a^{+}b R321=R310(R110)∗R120∣R320=(b∗a)(a∣ϵ)∗b∣⊘=b∗a+b
R 33 1 = R 31 0 ( R 11 0 ) ∗ R 13 0 ∣ R 33 0 = ( b ∗ a ) ( a ∣ ϵ ) ∗ ⊘ ∣ ϵ = ϵ R_{33}^{1} = R_{31}^{0} (R_{11}^{0})^{\ast} R_{13}^{0} | R_{33}^{0} = (b^{\ast}a) (a|\epsilon)^{\ast} \oslash | \epsilon = \epsilon R331=R310(R110)∗R130∣R330=(b∗a)(a∣ϵ)∗⊘∣ϵ=ϵ -
k = 2 k = 2 k=2
R 00 2 = R 02 1 ( R 22 1 ) ∗ R 20 1 ∣ R 00 1 = ( b ∗ a + b ) ( a + b ∣ ϵ ) ∗ ⊘ ∣ b ∗ = b ∗ R_{00}^{2} = R_{02}^{1} (R_{22}^{1})^{\ast} R_{20}^{1} | R_{00}^{1} = (b^{\ast}a^{+}b) (a^{+}b|\epsilon)^{\ast} \oslash | b^{\ast} = b^{\ast} R002=R021(R221)∗R201∣R001=(b∗a+b)(a+b∣ϵ)∗⊘∣b∗=b∗
R 01 2 = R 02 1 ( R 22 1 ) ∗ R 21 1 ∣ R 01 1 = ( b ∗ a + b ) ( a + b ∣ ϵ ) ∗ a + ∣ ( b ∗ a + ) = b ∗ a + ( ( b a + ) + ∣ ϵ ) R_{01}^{2} = R_{02}^{1} (R_{22}^{1})^{\ast} R_{21}^{1} | R_{01}^{1} = (b^{\ast}a^{+}b) (a^{+}b|\epsilon)^{\ast} a^{+} | (b^{\ast}a^{+}) = b^{\ast}a^{+}((ba^{+})^{+}|\epsilon) R012=R021(R221)∗R211∣R011=(b∗a+b)(a+b∣ϵ)∗a+∣(b∗a+)=b∗a+((ba+)+∣ϵ)
R 02 2 = R 02 1 ( R 22 1 ) ∗ R 22 1 ∣ R 02 1 = ( b ∗ a + b ) ( a + b ∣ ϵ ) ∗ ( a + b ∣ ϵ ) ∣ ( b ∗ a + b ) = b ∗ ( a + b ) + R_{02}^{2} = R_{02}^{1} (R_{22}^{1})^{\ast} R_{22}^{1} | R_{02}^{1} = (b^{\ast}a^{+}b) (a^{+}b|\epsilon)^{\ast} (a^{+}b|\epsilon) | (b^{\ast}a^{+}b) = b^{\ast}(a^{+}b)^{+} R022=R021(R221)∗R221∣R021=(b∗a+b)(a+b∣ϵ)∗(a+b∣ϵ)∣(b∗a+b)=b∗(a+b)+
R 03 2 = R 02 1 ( R 22 1 ) ∗ R 23 1 ∣ R 03 1 = ( b ∗ a + b ) ( a + b ∣ ϵ ) ∗ b ∣ ⊘ = b ∗ ( a + b ) + b R_{03}^{2} = R_{02}^{1} (R_{22}^{1})^{\ast} R_{23}^{1} | R_{03}^{1} = (b^{\ast}a^{+}b) (a^{+}b|\epsilon)^{\ast} b | \oslash = b^{\ast}(a^{+}b)^{+}b R032=R021(R221)∗R231∣R031=(b∗a+b)(a+b∣ϵ)∗b∣⊘=b∗(a+b)+b
R 10 2 = R 12 1 ( R 22 1 ) ∗ R 20 1 ∣ R 10 1 = ( a ∗ b ) ( a + b ∣ ϵ ) ∗ ⊘ ∣ ⊘ = ⊘ R_{10}^{2} = R_{12}^{1} (R_{22}^{1})^{\ast} R_{20}^{1} | R_{10}^{1} = (a^{\ast}b) (a^{+}b|\epsilon)^{\ast} \oslash | \oslash = \oslash R102=R121(R221)∗R201∣R101=(a∗b)(a+b∣ϵ)∗⊘∣⊘=⊘
R 11 2 = R 12 1 ( R 22 1 ) ∗ R 21 1 ∣ R 11 1 = ( a ∗ b ) ( a + b ∣ ϵ ) ∗ a + ∣ a ∗ = a ∗ ( ( b a + ) + ∣ ϵ ) R_{11}^{2} = R_{12}^{1} (R_{22}^{1})^{\ast} R_{21}^{1} | R_{11}^{1} = (a^{\ast}b) (a^{+}b|\epsilon)^{\ast} a^{+} | a^{\ast} = a^{\ast}((ba^{+})^{+}|\epsilon) R112=R121(R221)∗R211∣R111=(a∗b)(a+b∣ϵ)∗a+∣a∗=a∗((ba+)+∣ϵ)
R 12 2 = R 12 1 ( R 22 1 ) ∗ R 22 1 ∣ R 12 1 = ( a ∗ b ) ( a + b ∣ ϵ ) ∗ ( a + b ∣ ϵ ) ∣ ( a ∗ b ) = a ∗ b ( a + b ) ∗ R_{12}^{2} = R_{12}^{1} (R_{22}^{1})^{\ast} R_{22}^{1} | R_{12}^{1} = (a^{\ast}b) (a^{+}b|\epsilon)^{\ast} (a^{+}b|\epsilon) | (a^{\ast}b) = a^{\ast}b(a^{+}b)^{\ast} R122=R121(R221)∗R221∣R121=(a∗b)(a+b∣ϵ)∗(a+b∣ϵ)∣(a∗b)=a∗b(a+b)∗
R 13 2 = R 12 1 ( R 22 1 ) ∗ R 23 1 ∣ R 13 1 = ( a ∗ b ) ( a + b ∣ ϵ ) ∗ b ∣ ⊘ = a ∗ b ( a + b ) ∗ b R_{13}^{2} = R_{12}^{1} (R_{22}^{1})^{\ast} R_{23}^{1} | R_{13}^{1} = (a^{\ast}b) (a^{+}b|\epsilon)^{\ast} b | \oslash = a^{\ast}b(a^{+}b)^{\ast}b R132=R121(R221)∗R231∣R131=(a∗b)(a+b∣ϵ)∗b∣⊘=a∗b(a+b)∗b
R 20 2 = R 22 1 ( R 22 1 ) ∗ R 20 1 ∣ R 20 1 = ( a + b ∣ ϵ ) ( a + b ∣ ϵ ) ∗ ⊘ ∣ ⊘ = ⊘ R_{20}^{2} = R_{22}^{1} (R_{22}^{1})^{\ast} R_{20}^{1} | R_{20}^{1} = (a^{+}b|\epsilon) (a^{+}b|\epsilon)^{\ast} \oslash | \oslash = \oslash R202=R221(R221)∗R201∣R201=(a+b∣ϵ)(a+b∣ϵ)∗⊘∣⊘=⊘
R 21 2 = R 22 1 ( R 22 1 ) ∗ R 21 1 ∣ R 21 1 = ( a + b ∣ ϵ ) ( a + b ∣ ϵ ) ∗ a + ∣ a + = ( a + b ) ∗ a + R_{21}^{2} = R_{22}^{1} (R_{22}^{1})^{\ast} R_{21}^{1} | R_{21}^{1} = (a^{+}b|\epsilon) (a^{+}b|\epsilon)^{\ast} a^{+} | a^{+} = (a^{+}b)^{\ast}a^{+} R212=R221(R221)∗R211∣R211=(a+b∣ϵ)(a+b∣ϵ)∗a+∣a+=(a+b)∗a+
R 22 2 = R 22 1 ( R 22 1 ) ∗ R 22 1 ∣ R 22 1 = ( a + b ∣ ϵ ) ( a + b ∣ ϵ ) ∗ ( a + b ∣ ϵ ) ∣ ( a + b ∣ ϵ ) = ( a + b ) ∗ R_{22}^{2} = R_{22}^{1} (R_{22}^{1})^{\ast} R_{22}^{1} | R_{22}^{1} = (a^{+}b|\epsilon) (a^{+}b|\epsilon)^{\ast} (a^{+}b|\epsilon) | (a^{+}b|\epsilon) = (a^{+}b)^{\ast} R222=R221(R221)∗R221∣R221=(a+b∣ϵ)(a+b∣ϵ)∗(a+b∣ϵ)∣(a+b∣ϵ)=(a+b)∗
R 23 2 = R 22 1 ( R 22 1 ) ∗ R 23 1 ∣ R 23 1 = ( a + b ∣ ϵ ) ( a + b ∣ ϵ ) ∗ b ∣ b = ( a + b ) ∗ b R_{23}^{2} = R_{22}^{1} (R_{22}^{1})^{\ast} R_{23}^{1} | R_{23}^{1} = (a^{+}b|\epsilon) (a^{+}b|\epsilon)^{\ast} b | b = (a^{+}b)^{\ast}b R232=R221(R221)∗R231∣R231=(a+b∣ϵ)(a+b∣ϵ)∗b∣b=(a+b)∗b
R 30 2 = R 32 1 ( R 22 1 ) ∗ R 20 1 ∣ R 30 1 = ( b ∗ a + b ) ( a + b ∣ ϵ ) ∗ ⊘ ∣ b ∗ = b ∗ R_{30}^{2} = R_{32}^{1} (R_{22}^{1})^{\ast} R_{20}^{1} | R_{30}^{1} = (b^{\ast}a^{+}b) (a^{+}b|\epsilon)^{\ast} \oslash | b^{\ast} = b^{\ast} R302=R321(R221)∗R201∣R301=(b∗a+b)(a+b∣ϵ)∗⊘∣b∗=b∗
R 31 2 = R 32 1 ( R 22 1 ) ∗ R 21 1 ∣ R 31 1 = ( b ∗ a + b ) ( a + b ∣ ϵ ) ∗ a + ∣ ( b ∗ a + ) = b ∗ ( a + b ) ∗ a + R_{31}^{2} = R_{32}^{1} (R_{22}^{1})^{\ast} R_{21}^{1} | R_{31}^{1} = (b^{\ast}a^{+}b) (a^{+}b|\epsilon)^{\ast} a^{+} | (b^{\ast}a^{+}) = b^{\ast}(a^{+}b)^{\ast}a^{+} R312=R321(R221)∗R211∣R311=(b∗a+b)(a+b∣ϵ)∗a+∣(b∗a+)=b∗(a+b)∗a+
R 32 2 = R 32 1 ( R 22 1 ) ∗ R 22 1 ∣ R 32 1 = ( b ∗ a + b ) ( a + b ∣ ϵ ) ∗ ( a + b ∣ ϵ ) ∣ ( b ∗ a + b ) = b ∗ ( a + b ) + R_{32}^{2} = R_{32}^{1} (R_{22}^{1})^{\ast} R_{22}^{1} | R_{32}^{1} = (b^{\ast}a^{+}b) (a^{+}b|\epsilon)^{\ast} (a^{+}b|\epsilon) | (b^{\ast}a^{+}b) = b^{\ast}(a^{+}b)^{+} R322=R321(R221)∗R221∣R321=(b∗a+b)(a+b∣ϵ)∗(a+b∣ϵ)∣(b∗a+b)=b∗(a+b)+
R 33 2 = R 32 1 ( R 22 1 ) ∗ R 23 1 ∣ R 33 1 = ( b ∗ a + b ) ( a + b ∣ ϵ ) ∗ b ∣ ϵ = b ∗ ( a + b ) + ∣ ϵ R_{33}^{2} = R_{32}^{1} (R_{22}^{1})^{\ast} R_{23}^{1} | R_{33}^{1} = (b^{\ast}a^{+}b) (a^{+}b|\epsilon)^{\ast} b | \epsilon = b^{\ast}(a^{+}b)^{+}|\epsilon R332=R321(R221)∗R231∣R331=(b∗a+b)(a+b∣ϵ)∗b∣ϵ=b∗(a+b)+∣ϵ -
k = 3 k = 3 k=3
R 00 3 = R 03 2 ( R 33 2 ) ∗ R 30 2 ∣ R 00 2 = ( b ∗ ( a + b ) + b ) ( b ∗ ( a + b ) + ∣ ϵ ) ∗ b ∗ ∣ b ∗ R_{00}^{3} = R_{03}^{2} (R_{33}^{2})^{\ast} R_{30}^{2} | R_{00}^{2} = (b^{\ast}(a^{+}b)^{+}b) (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} b^{\ast} | b^{\ast} R003=R032(R332)∗R302∣R002=(b∗(a+b)+b)(b∗(a+b)+∣ϵ)∗b∗∣b∗
R 01 3 = R 03 2 ( R 33 2 ) ∗ R 31 2 ∣ R 01 2 = ( b ∗ ( a + b ) + b ) ( b ∗ ( a + b ) + ∣ ϵ ) ∗ b ∗ ( a + b ) ∗ a + ∣ b ∗ a + ( ( b a + ) + ∣ ϵ ) R_{01}^{3} = R_{03}^{2} (R_{33}^{2})^{\ast} R_{31}^{2} | R_{01}^{2} = (b^{\ast}(a^{+}b)^{+}b) (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} b^{\ast}(a^{+}b)^{\ast}a^{+} | b^{\ast}a^{+}((ba^{+})^{+}|\epsilon) R013=R032(R332)∗R312∣R012=(b∗(a+b)+b)(b∗(a+b)+∣ϵ)∗b∗(a+b)∗a+∣b∗a+((ba+)+∣ϵ)
R 02 3 = R 03 2 ( R 33 2 ) ∗ R 32 2 ∣ R 02 2 = ( b ∗ ( a + b ) + b ) ( b ∗ ( a + b ) + ∣ ϵ ) ∗ b ∗ ( a + b ) + ∣ b ∗ ( a + b ) + R_{02}^{3} = R_{03}^{2} (R_{33}^{2})^{\ast} R_{32}^{2} | R_{02}^{2} = (b^{\ast}(a^{+}b)^{+}b) (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} b^{\ast}(a^{+}b)^{+} | b^{\ast}(a^{+}b)^{+} R023=R032(R332)∗R322∣R022=(b∗(a+b)+b)(b∗(a+b)+∣ϵ)∗b∗(a+b)+∣b∗(a+b)+
R 03 3 = R 03 2 ( R 33 2 ) ∗ R 33 2 ∣ R 03 2 = ( b ∗ ( a + b ) + b ) ( b ∗ ( a + b ) + ∣ ϵ ) ∗ ( b ∗ ( a + b ) + ∣ ϵ ) ∣ b ∗ ( a + b ) + b R_{03}^{3} = R_{03}^{2} (R_{33}^{2})^{\ast} R_{33}^{2} | R_{03}^{2} = (b^{\ast}(a^{+}b)^{+}b) (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} (b^{\ast}(a^{+}b)^{+}|\epsilon) | b^{\ast}(a^{+}b)^{+}b R033=R032(R332)∗R332∣R032=(b∗(a+b)+b)(b∗(a+b)+∣ϵ)∗(b∗(a+b)+∣ϵ)∣b∗(a+b)+b
R 10 3 = R 13 2 ( R 33 2 ) ∗ R 30 2 ∣ R 10 2 = ( a ∗ b ( a + b ) ∗ b ) ( b ∗ ( a + b ) + ∣ ϵ ) ∗ b ∗ ∣ ⊘ R_{10}^{3} = R_{13}^{2} (R_{33}^{2})^{\ast} R_{30}^{2} | R_{10}^{2} = (a^{\ast}b(a^{+}b)^{\ast}b) (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} b^{\ast} | \oslash R103=R132(R332)∗R302∣R102=(a∗b(a+b)∗b)(b∗(a+b)+∣ϵ)∗b∗∣⊘
R 11 3 = R 13 2 ( R 33 2 ) ∗ R 31 2 ∣ R 11 2 = ( a ∗ b ( a + b ) ∗ b ) ( b ∗ ( a + b ) + ∣ ϵ ) ∗ b ∗ ( a + b ) ∗ a + ∣ a ∗ ( ( b a + ) + ∣ ϵ ) R_{11}^{3} = R_{13}^{2} (R_{33}^{2})^{\ast} R_{31}^{2} | R_{11}^{2} = (a^{\ast}b(a^{+}b)^{\ast}b) (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} b^{\ast}(a^{+}b)^{\ast}a^{+} | a^{\ast}((ba^{+})^{+}|\epsilon) R113=R132(R332)∗R312∣R112=(a∗b(a+b)∗b)(b∗(a+b)+∣ϵ)∗b∗(a+b)∗a+∣a∗((ba+)+∣ϵ)
R 12 3 = R 13 2 ( R 33 2 ) ∗ R 32 2 ∣ R 12 2 = ( a ∗ b ( a + b ) ∗ b ) ( b ∗ ( a + b ) + ∣ ϵ ) ∗ b ∗ ( a + b ) + ∣ a ∗ b ( a + b ) ∗ R_{12}^{3} = R_{13}^{2} (R_{33}^{2})^{\ast} R_{32}^{2} | R_{12}^{2} = (a^{\ast}b(a^{+}b)^{\ast}b) (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} b^{\ast}(a^{+}b)^{+} | a^{\ast}b(a^{+}b)^{\ast} R123=R132(R332)∗R322∣R122=(a∗b(a+b)∗b)(b∗(a+b)+∣ϵ)∗b∗(a+b)+∣a∗b(a+b)∗
R 13 3 = R 13 2 ( R 33 2 ) ∗ R 33 2 ∣ R 13 2 = ( a ∗ b ( a + b ) ∗ b ) ( b ∗ ( a + b ) + ∣ ϵ ) ∗ ( b ∗ ( a + b ) + ∣ ϵ ) ∣ a ∗ b ( a + b ) ∗ b R_{13}^{3} = R_{13}^{2} (R_{33}^{2})^{\ast} R_{33}^{2} | R_{13}^{2} = (a^{\ast}b(a^{+}b)^{\ast}b) (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} (b^{\ast}(a^{+}b)^{+}|\epsilon) | a^{\ast}b(a^{+}b)^{\ast}b R133=R132(R332)∗R332∣R132=(a∗b(a+b)∗b)(b∗(a+b)+∣ϵ)∗(b∗(a+b)+∣ϵ)∣a∗b(a+b)∗b
R 20 3 = R 23 2 ( R 33 2 ) ∗ R 30 2 ∣ R 20 2 = ( a + b ) ∗ b ( b ∗ ( a + b ) + ∣ ϵ ) ∗ b ∗ ∣ ⊘ R_{20}^{3} = R_{23}^{2} (R_{33}^{2})^{\ast} R_{30}^{2} | R_{20}^{2} = (a^{+}b)^{\ast}b (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} b^{\ast} | \oslash R203=R232(R332)∗R302∣R202=(a+b)∗b(b∗(a+b)+∣ϵ)∗b∗∣⊘
R 21 3 = R 23 2 ( R 33 2 ) ∗ R 31 2 ∣ R 21 2 = ( a + b ) ∗ b ( b ∗ ( a + b ) + ∣ ϵ ) ∗ b ∗ ( a + b ) ∗ a + ∣ ( a + b ) ∗ a + R_{21}^{3} = R_{23}^{2} (R_{33}^{2})^{\ast} R_{31}^{2} | R_{21}^{2} = (a^{+}b)^{\ast}b (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} b^{\ast}(a^{+}b)^{\ast}a^{+} | (a^{+}b)^{\ast}a^{+} R213=R232(R332)∗R312∣R212=(a+b)∗b(b∗(a+b)+∣ϵ)∗b∗(a+b)∗a+∣(a+b)∗a+
R 22 3 = R 23 2 ( R 33 2 ) ∗ R 32 2 ∣ R 22 2 = ( a + b ) ∗ b ( b ∗ ( a + b ) + ∣ ϵ ) ∗ b ∗ ( a + b ) + ∣ ( a + b ) ∗ R_{22}^{3} = R_{23}^{2} (R_{33}^{2})^{\ast} R_{32}^{2} | R_{22}^{2} = (a^{+}b)^{\ast}b (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} b^{\ast}(a^{+}b)^{+} | (a^{+}b)^{\ast} R223=R232(R332)∗R322∣R222=(a+b)∗b(b∗(a+b)+∣ϵ)∗b∗(a+b)+∣(a+b)∗
R 23 3 = R 23 2 ( R 33 2 ) ∗ R 33 2 ∣ R 23 2 = ( a + b ) ∗ b ( b ∗ ( a + b ) + ∣ ϵ ) ∗ ( b ∗ ( a + b ) + ∣ ϵ ) ∣ ( a + b ) ∗ b R_{23}^{3} = R_{23}^{2} (R_{33}^{2})^{\ast} R_{33}^{2} | R_{23}^{2} = (a^{+}b)^{\ast}b (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} (b^{\ast}(a^{+}b)^{+}|\epsilon) | (a^{+}b)^{\ast}b R233=R232(R332)∗R332∣R232=(a+b)∗b(b∗(a+b)+∣ϵ)∗(b∗(a+b)+∣ϵ)∣(a+b)∗b
R 30 3 = R 33 2 ( R 33 2 ) ∗ R 30 2 ∣ R 30 2 = ( b ∗ ( a + b ) + ∣ ϵ ) ( b ∗ ( a + b ) + ∣ ϵ ) ∗ b ∗ ∣ b ∗ R_{30}^{3} = R_{33}^{2} (R_{33}^{2})^{\ast} R_{30}^{2} | R_{30}^{2} = (b^{\ast}(a^{+}b)^{+}|\epsilon) (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} b^{\ast} | b^{\ast} R303=R332(R332)∗R302∣R302=(b∗(a+b)+∣ϵ)(b∗(a+b)+∣ϵ)∗b∗∣b∗
R 31 3 = R 33 2 ( R 33 2 ) ∗ R 31 2 ∣ R 31 2 = ( b ∗ ( a + b ) + ∣ ϵ ) ( b ∗ ( a + b ) + ∣ ϵ ) ∗ b ∗ ( a + b ) ∗ a + ∣ b ∗ ( a + b ) ∗ a + R_{31}^{3} = R_{33}^{2} (R_{33}^{2})^{\ast} R_{31}^{2} | R_{31}^{2} = (b^{\ast}(a^{+}b)^{+}|\epsilon) (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} b^{\ast}(a^{+}b)^{\ast}a^{+} | b^{\ast}(a^{+}b)^{\ast}a^{+} R313=R332(R332)∗R312∣R312=(b∗(a+b)+∣ϵ)(b∗(a+b)+∣ϵ)∗b∗(a+b)∗a+∣b∗(a+b)∗a+
R 32 3 = R 33 2 ( R 33 2 ) ∗ R 32 2 ∣ R 32 2 = ( b ∗ ( a + b ) + ∣ ϵ ) ( b ∗ ( a + b ) + ∣ ϵ ) ∗ b ∗ ( a + b ) + ∣ b ∗ ( a + b ) + R_{32}^{3} = R_{33}^{2} (R_{33}^{2})^{\ast} R_{32}^{2} | R_{32}^{2} = (b^{\ast}(a^{+}b)^{+}|\epsilon) (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} b^{\ast}(a^{+}b)^{+} | b^{\ast}(a^{+}b)^{+} R323=R332(R332)∗R322∣R322=(b∗(a+b)+∣ϵ)(b∗(a+b)+∣ϵ)∗b∗(a+b)+∣b∗(a+b)+
R 33 3 = R 33 2 ( R 33 2 ) ∗ R 33 2 ∣ R 33 2 = ( b ∗ ( a + b ) + ∣ ϵ ) ( b ∗ ( a + b ) + ∣ ϵ ) ∗ ( b ∗ ( a + b ) + ∣ ϵ ) ∣ b ∗ ( a + b ) + ∣ ϵ R_{33}^{3} = R_{33}^{2} (R_{33}^{2})^{\ast} R_{33}^{2} | R_{33}^{2} = (b^{\ast}(a^{+}b)^{+}|\epsilon) (b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast} (b^{\ast}(a^{+}b)^{+}|\epsilon) | b^{\ast}(a^{+}b)^{+}|\epsilon R333=R332(R332)∗R332∣R332=(b∗(a+b)+∣ϵ)(b∗(a+b)+∣ϵ)∗(b∗(a+b)+∣ϵ)∣b∗(a+b)+∣ϵ
最后的
k
=
3
k = 3
k=3 就不展开了,我们只需要简化
R
03
3
R_{03}^{3}
R033 就可以了:
由
R
03
3
=
(
b
∗
(
a
+
b
)
+
b
)
(
b
∗
(
a
+
b
)
+
∣
ϵ
)
∗
(
b
∗
(
a
+
b
)
+
∣
ϵ
)
∣
b
∗
(
a
+
b
)
+
b
R_{03}^{3} = (b^{\ast}(a^{+}b)^{+}b)(b^{\ast}(a^{+}b)^{+}|\epsilon)^{\ast}(b^{\ast}(a^{+}b)^{+}|\epsilon)|b^{\ast}(a^{+}b)^{+}b
R033=(b∗(a+b)+b)(b∗(a+b)+∣ϵ)∗(b∗(a+b)+∣ϵ)∣b∗(a+b)+b
=
b
∗
(
a
+
b
)
+
b
(
b
∗
(
a
+
b
)
+
)
∗
= b^{\ast}(a^{+}b)^{+}b(b^{\ast}(a^{+}b)^{+})^{\ast}
=b∗(a+b)+b(b∗(a+b)+)∗
=
b
∗
a
∗
a
b
(
a
∗
a
b
)
∗
b
(
b
∗
a
∗
a
b
(
a
∗
a
b
)
∗
)
∗
= b^{\ast}a^{\ast}ab(a^{\ast}ab)^{\ast}b(b^{\ast}a^{\ast}ab(a^{\ast}ab)^{\ast})^{\ast}
=b∗a∗ab(a∗ab)∗b(b∗a∗ab(a∗ab)∗)∗
=
b
∗
(
a
∗
a
b
)
∗
a
∗
a
b
b
(
b
∗
(
a
∗
a
b
)
∗
a
∗
a
b
)
∗
= b^{\ast}(a^{\ast}ab)^{\ast}a^{\ast}abb(b^{\ast}(a^{\ast}ab)^{\ast}a^{\ast}ab)^{\ast}
=b∗(a∗ab)∗a∗abb(b∗(a∗ab)∗a∗ab)∗
=
(
a
∣
b
)
∗
a
b
b
= (a|b)^{*}abb
=(a∣b)∗abb
有点偷吃步hhh,不过反正结果上是一样的,这样的 Kleene 闭包也是可以自动化的所以不需要过于纠结必须用手算hh。
最终版本的 DFA
到此就全部完成啦,我们经由 RE -> NFA -> DFA -> 最小化 DFA -> 验证 DFA 这几个步骤,终于构建出了最终版本的 DFA 了,撒花~
示例1: a ( b ∣ c ) ∗ a(b|c)^{*} a(b∣c)∗

示例2: ( a ∣ b ) ∗ a b b (a|b)^{*}abb (a∣b)∗abb

结语
从 RE 构建 DFA 的三部曲就到这边结束啦,由于最后的验证 DFA使用 Kleene 闭包其实比较繁琐,读者可以尝试自己实现自动化这个过程的程序(作者估计是写不出来了hhh)。






















 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








