计算机组成原理：定点数和浮点数、校验码

1、定点数和浮点数

小数点在计算器中并没有专门的器件进行存放。根据小数点的位置是否固定，可将数字分为定点数和浮点数。

定点数

定点数是小数点位置固定的数，小数点的位置由事先约定。同一种定点数的机器码中，每一位的权值都是相同的。
约定小数点在最低数值位之后的定点数称为定点纯整数；在最高数值位之前的称为定点纯小数。采用定点数的机器称为定点机。
设8位机器码，其中最高位为符号位。
对于定点整数机：
原码和反码的数值范围：-2⁷ + 1 ~ 2⁷ - 1
补码的数值范围：-2⁷ ~ 2⁷ - 1
对于定点小数机：
原码和反码的数值范围：-1 + 2^-7 ~ 1 - 2^-7
补码的数值范围：-1 ~ 1 - 2^-7

当数值超出定点数所能表示的范围时，称为溢出。

浮点数

浮点数是小数点位置不固定的数。
浮点数在计算机中由两个部分组成：阶码和尾数。

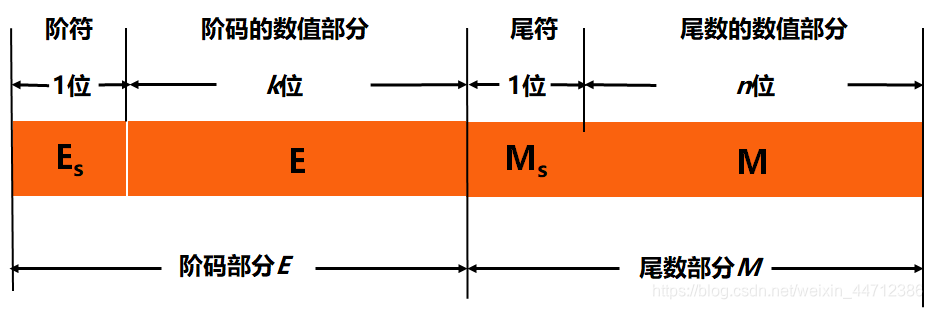
其中，尾数表示数值的有效数字，阶码指出小数点的位置。
对于阶码共k + 1位，尾数共n + 1位的浮点数(均包含符号)：
最大正数：(1 - 2^-n) * 2^{2^k-1}
最小负数&