Non-Local Recurrent Network for Image Restoration
文章链接: NLRNDing Liu, Bihan Wen, Y uchen Fan, Chen Change Loy, and Thomas S Huang. Non-local recurrent network for image restoration. In NIPS, 2018. 2, 4, 5, 7
摘要:很多传统方法已经证实了非局部相似性作为先验信息对图像恢复的有效性,但通过深度神经网络充分利用这种内在属性仍然存在一定的困难。本文提出了一种非局部的递归网络首次将得局部操作和递归网络相融合,本文的主要共享有以下几点: 1.比起目前单独获取自相似性的手段不同,本文的非局部模块可以自由的嵌入到现有的网络结构中,进行端到端的训练。2.充分利用了RNN机构的参数效率,让深度特征能够沿着相邻的循环状态进行传播。3.本文证明了在计算给定退化图像的深度特征相关性时,最重要的是保持一个有限的邻域
1.Introduction
图像复原可以分为不同的子问题如图像去噪和图像超分辨,图像恢复的关键是基于图像先验的正则化设计,过去的研究中局部和非局部图像先验被广泛的使用,以图像去噪为例,早期大多使用高斯滤波和基于全变差的方法等局部图像先验,之后,自然图像自相似性引起了广泛关注,发展出基于非局部的方法如非局部均值,协同滤波,联合稀疏和低秩建模等方法,这些非局部方法在提取非局部块之间的关系提高图像恢复质量方面表现出优秀的结果。
尽管非局部自相似性被广泛研究,但很少有深度学习的方法研究提取此属性,卷积神经网络的方法虽然达到了令人印象深刻的结果但仍然没有明确使用图像的自相似属性,为了改良此弱点,一些研究在图像块输入卷积网络之前对块进行了匹配,然而快匹配的步骤是孤立的,不能与网络进行联合训练。
本文首次将CNN中的 非局部操作用于图像恢复,提出了非局部递归网络NLRN,首先设计了非局部模块提取退化图像特征关系作为自相似性测量,此模块能够灵活的嵌入到现有的神经网络中。且在不影响恢复质量的情况下,为提高参数效率本文采用了递归神经网络结构。其次,本文研究了深度特征空间中的非局部操作,发现限制局部关系的计算提高了退化图像的鲁棒性。受限的邻域有助于空间中距离相近的相关特征的计算,过滤噪声特征。最后,本方法能让非局部操作的信息在相邻的递归状态之间进行传递,这种内部特征相关性的流动有助于更鲁棒的相关性估计。通过联合非局部操作和典型的卷积,本文的NLRN能够有效的提取和使用图像的局部和非局部属性来进行图像恢复。
本文的工作与Non-local neural Nerwork有很大的区别,对特征的每个位置来说,本文只在其邻域采集其特征相关性,并不会在整个图像进行非局部操作,而且在实验中,证明了依赖于局部区域的深度特征在计算非局部先验时更可能是有效的。另外对于退化测量结果来看,更大的邻域甚至整个图像可能导致不精确的相关性估计,最后本文的方法充分利用了RNN结构中相关性信息可以在相邻状态之间传递的优点,增加了对不同层次退化特征相关性估计的鲁棒性。
Related Work
略。。。。。
3.Non-local Operations for Image Restoration
3.1 A General Framework
非局部操作以多通道的输入
X
∈
R
N
×
m
X\in R^{N\times m}
X∈RN×m作为图像特征,生成输出特征
Z
∈
R
N
×
k
Z\in R^{N\times k}
Z∈RN×k,这里的N和m表示图像像素的个数和数据的通道数,将其用公式表示为:
Z
=
d
i
a
g
(
δ
(
X
)
−
1
)
Φ
(
X
)
G
(
X
)
Z=diag( { \delta (X)}^{-1})\Phi(X)G(X)
Z=diag(δ(X)−1)Φ(X)G(X),
Φ
(
X
)
∈
R
N
×
N
(
1
)
\Phi(X)\in R^{N\times N} (1)
Φ(X)∈RN×N(1)
是非局部关系矩阵,
G
(
X
)
∈
R
N
×
k
G(X)\in R^{N\times k}
G(X)∈RN×k是多通道非局部变换,每个行向量
X
i
X_{i}
Xi表示i位置的局部特征,
Φ
(
X
)
i
j
\Phi(X)^{j}_{i}
Φ(X)ij表示
X
i
和
X
j
X_{i}和X_{j}
Xi和Xj之间的关系,每个
G
(
X
)
j
G(X)_{j}
G(X)j的行向量表示
X
j
X_{j}
Xj的嵌入变形,对角矩阵
d
i
a
g
Φ
(
X
)
∈
R
N
×
N
diag{\Phi(X)}\in R^{N\times N}
diagΦ(X)∈RN×N用归一化因子
Φ
i
(
X
)
\Phi_{i}(X)
Φi(X)对第i个像素进行归一化。
3.2 Classic Methods
Blocking matching(BM)块匹配是传统方法中利用非局部图像结构的常用方法,一个q*q空间邻域被设置为每个i位置的中心,且
X
i
X_{i}
Xi减少至以i为中心的图像块,BM从邻域中选
K
i
K_{i}
Ki个最相似的图像块,以此来联合恢复
X
i
X_{i}
Xi,在本文的非局部框架下,这些操作可以表示为:
Z
i
=
1
δ
i
(
X
)
∑
j
∈
C
i
Φ
(
X
)
i
j
G
(
X
)
j
,
∀
i
Z_{i}=\frac{1}{\delta_{i}(X)}\sum_{j\in C_{i}}\Phi(X)_{i}^{j}G(X)_{j},\forall i
Zi=δi(X)1∑j∈CiΦ(X)ijG(X)j,∀i (2)
这里
δ
i
(
X
)
=
∑
j
∈
C
i
Φ
(
X
)
j
i
\delta_{i}(X)=\sum_{j\in C_{i}}\Phi(X)_{j}^{i}
δi(X)=∑j∈CiΦ(X)ji和
C
i
C_{i}
Ci表示第
K
i
K_{i}
Ki个块的索引,因此每个行
Φ
(
X
)
i
\Phi(X)_{i}
Φ(X)i只有非零项,在不同模型的非局部方法中嵌入项G(X)和非零相变量是不同的,
3.3 Non-Local Module
基于公式1的框架,本文提出了另一种匹配方法,用高斯核和欧式距离作为距离度量,线性嵌入定义如下:
Φ
(
X
)
i
j
=
ø
(
X
i
,
X
j
)
=
e
x
p
{
θ
(
X
i
)
ψ
(
X
j
)
T
}
,
∀
i
,
j
\Phi(X)^{j}_{i}=\text{\o}(X_{i},X_{j})=exp \left \{ \theta(X_{i})\psi(X_{j})^{T} \right \},\forall i,j
Φ(X)ij=ø(Xi,Xj)=exp{θ(Xi)ψ(Xj)T},∀i,j
θ
(
X
i
)
=
X
i
W
θ
,
ψ
(
X
i
)
=
X
i
W
ψ
,
G
(
X
)
i
=
X
i
W
g
,
∀
i
\theta(X_{i})=X_{i}W_{\theta},\psi(X_{i})=X_{i}W_{\psi},G(X)_{i}=X_{i}W_{g},\forall i
θ(Xi)=XiWθ,ψ(Xi)=XiWψ,G(X)i=XiWg,∀i
嵌入变换
W
θ
,
W
ø
,
W
g
W_{\theta},W_{\text{\o}},W_{g}
Wθ,Wø,Wg都是学习到的,且形状分别为ml,ml,mm,因此非局部操作可以表示为:
Z
i
=
1
δ
i
(
X
)
∑
j
∈
S
i
e
x
p
{
X
i
W
θ
W
ψ
T
X
j
T
}
X
i
W
g
,
∀
i
Z_{i}=\frac{1}{\delta_{i}(X)}\sum_{j\in S_{i}}exp\left\{X_{i}W_{\theta}W_{\psi}^{T}X_{j}^{T} \right\}X_{i}W_{g},\forall i
Zi=δi(X)1∑j∈Siexp{XiWθWψTXjT}XiWg,∀i
上式的
δ
i
(
X
)
=
∑
j
∈
S
i
ø
(
X
i
,
X
j
)
\delta_{i}(X)=\sum_{j\in S_{i}}\text{\o}(X_{i},X_{j})
δi(X)=∑j∈Siø(Xi,Xj)表示
X
i
和
邻
域
S
i
中
的
X
j
X_{i}和邻域S_{i}中的X_{j}
Xi和邻域Si中的Xj之间的关系,
本文提出的非局部操作通过可微分操作实现,因此可以和神经网络联合学习,本文通过跳跃链接将非局部操作包装成模块,如下图所示:
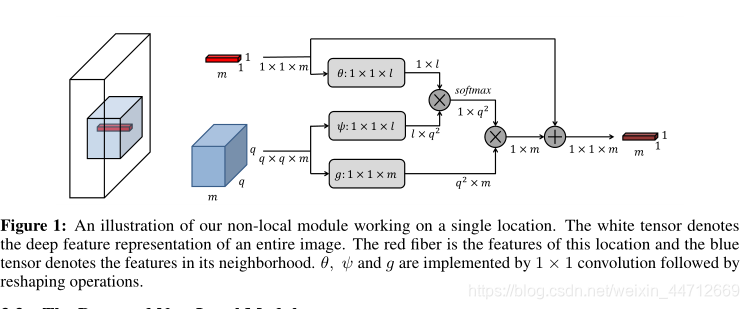
跳跃链接能使本模块插入到任何预训练模块当中,且通过将
W
g
W_{g}
Wg初始化为0来保持其初始的参数,此模块只引入了参数
θ
,
ψ
,
g
\theta,\psi,g
θ,ψ,g作为11的卷积,其每个位置的输出只取决与q*q大小的邻域,可以跟任意大小的输入相结合。
Relation to Other Methods:
最近的研究将非局部块匹配操作和神经网络结合用于图像恢复,但传统的方法直接对退化的输入图像块进行操作,对于严重退化的图像是不准确的,而本文提出的非局部操作能够应用于对退化更加鲁棒的学习得到的深度特征,更重要的是,本文提出的模块能够与神经网络一起进行端到端的训练,而传统方法只能作为独立结果。
本文的方法与Non-local neural Network不同,其在整幅图像上计算特征相关性,相当于本文方法中的邻域扩大到整幅图像,经验表明增加邻域尺寸并不能提高图像恢复的结果,因此必须选择一个合适大小的邻域,且其方法只能针对一个固定尺寸的输入,而本文的方法能够适应不同尺寸。
4.Non-Local Recurrent Network
本文的RNN框架由一组状态组成,输入,输出,循环以及转台之间的转换函数,输入、输出、循环分别可表示为:x,y,s,每隔t步,RNN接收到一个输入
x
t
x^{t}
xt,循环和输出如下:
S
t
=
f
i
n
p
u
t
(
x
t
)
+
f
r
e
c
u
r
r
e
n
t
(
S
t
−
1
)
,
y
t
=
f
o
u
t
p
u
t
(
S
t
)
S^{t}=f_{input}(x^{t})+f_{recurrent}(S^{t-1}),y^{t}=f_{output}(S^{t})
St=finput(xt)+frecurrent(St−1),yt=foutput(St)每次更新
f
i
n
p
u
t
,
f
o
u
t
p
u
t
,
f
r
e
c
u
r
r
e
n
t
f_{input},f_{output},f_{recurrent}
finput,foutput,frecurrent
在本文的NLRN结构中:
1.
S
0
S^{0}
S0输入图像的映射
2.
x
t
=
0
,
∀
t
∈
1
,
.
.
.
.
.
.
,
T
,
a
n
d
f
i
n
p
u
t
(
0
)
=
0
x^{t}=0,\forall t\in{1,......,T},and f_{input}(0)=0
xt=0,∀t∈1,......,T,andfinput(0)=0
3.输出状态
y
t
y^{t}
yt只在最后的T时刻表示输出
非局部操作中的权重和卷积相同在循环状态共享,因此能够保持较高的参数效率
如下图所示:

在非局部模块中,来自之前状态i位置的特征相关性
s
c
o
r
r
t
−
1
s^{t-1}_{corr}
scorrt−1,**在标准化之前被添加到了当前的特征相关性中,这使得相邻状态之间的相关性估计更加可靠,**细节如下图所示



























 1881
1881

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








