Transformer 整体代码结构分析-CSDN博客

本文链接：https://blog.csdn.net/weixin_44714085/article/details/147426716

整体架构图

Embeddings(词嵌入实现)

import math
import torch.nn as nn

class Embeddings(nn.Module):
    """
    Transformer 词嵌入层实现（模型输入的第一层）
    
    █ 类的作用定位：
      - 上游：直接接收原始输入的词索引序列（如经过Tokenizer处理的整数序列）
      - 下游：输出给位置编码层（PositionalEncoding）进行向量叠加
      - 整体：将离散符号转化为连续向量空间表示的核心组件
    
    █ 数学公式：
      Embedding(x) = lookup(W, x) * sqrt(d_model)
      其中 W ∈ ℝ^(vocab_size × d_model) 是可学习的嵌入矩阵
    
    █ 初始化参数说明：
      | 参数名    | 类型 | 说明                     | 示例值      |
      |-----------|------|--------------------------|-------------|
      | d_model   | int  | 词向量维度（与Transformer隐藏层维度一致） | 512         |
      | vocab     | int  | 词汇表大小（包含所有可能的词索引）       | 10000       |
    """

    def __init__(self, d_model, vocab):
        super(Embeddings, self).__init__()
        """
        初始化词嵌入层结构
        
        █ 关键组件说明：
          lut (nn.Embedding): 
            核心嵌入层，实现索引到向量的映射
            权重矩阵形状：[vocab_size, d_model]
            
            工作原理示意图：
            输入索引: [2] 
            嵌入矩阵: [[0.1, 0.2, ...],  # 索引0的向量
                      [0.3, 0.5, ...],  # 索引1的向量
                      [0.7, 0.6, ...]]  # 索引2的向量
            输出向量: [0.7, 0.6, ...] * sqrt(d_model)
        """
        self.lut = nn.Embedding(vocab, d_model)  # 创建可训练的嵌入矩阵
        self.d_model = d_model  # 保存维度用于后续缩放

    def forward(self, x):
        """
        前向传播过程（维度变化图示）
        
        █ 输入输出规格：
          输入形状: [batch_size, seq_len]      示例：torch.Size([32, 50])
          输出形状: [batch_size, seq_len, d_model] 示例：torch.Size([32, 50, 512])
        
        █ 处理步骤分解：
          原始输入（示例）：
          [[ 101,  205, 3043, ...,   0],   # 句子1的索引序列
           [ 209, 5023,  876, ...,  102]]  # 句子2的索引序列
          
          步骤1：通过lut进行嵌入查找
          每个索引替换为对应的d_model维向量
          示例中间结果形状：[32, 50, 512]
          
          步骤2：缩放操作（数学证明必要性）：
          假设d_model=512，sqrt(512)≈22.627
          缩放使嵌入向量与后续位置编码的数值范围匹配
        """
        # 可视化中间过程（假设输入为 [[1,2],[3,4]]）
        # print("输入索引:\n", x)
        embeddings = self.lut(x)          # 嵌入查找
        # print("查找后的原始嵌入:\n", embeddings[0,:2])
        scaled_embeddings = embeddings * math.sqrt(self.d_model)  # 缩放
        # print("缩放后的嵌入:\n", scaled_embeddings[0,:2])
        return scaled_embeddings

# 单元测试示例
if __name__ == "__main__":
    # 参数设置
    vocab_size = 10000  # 假设词汇表包含10000个词
    d_model = 512       # 使用标准Transformer-base的维度
    
    # 初始化嵌入层
    embedding_layer = Embeddings(d_model, vocab_size)
    
    # 模拟输入（batch_size=2, seq_len=5）
    input_indices = torch.LongTensor([
        [101, 205, 3043, 0, 0],    # 句子1（0为padding）
        [209, 5023, 876, 102, 0]   # 句子2 
    ])
    
    print("输入索引矩阵形状:", input_indices.shape)
    output = embedding_layer(input_indices)
    print("输出嵌入矩阵形状:", output.shape)
    
    # 展示第一个词的处理过程
    print("\n示例词处理细节：")
    print("输入索引:", input_indices[0][0].item())
    print("对应的嵌入向量（前5维）:", output[0][0][:5].detach().numpy())
    print("缩放系数:", math.sqrt(d_model))

"""
预期输出：
输入索引矩阵形状: torch.Size([2, 5])
输出嵌入矩阵形状: torch.Size([2, 5, 512])

示例词处理细节：
输入索引: 101
对应的嵌入向量（前5维）: [ 0.023 -0.017  0.041  0.008 -0.052]（实际值随机）
缩放系数: 22.62741699797
"""

关键概念图解

嵌入矩阵工作原理

# 假设词汇表大小为5，d_model=3
嵌入矩阵 = [
    [0.1, 0.2, 0.3],  # 索引0
    [0.4, 0.5, 0.6],  # 索引1
    [0.7, 0.8, 0.9],  # 索引2
    [1.0, 1.1, 1.2],  # 索引3 
    [1.3, 1.4, 1.5]   # 索引4
]

输入序列 = [2, 0, 3]
输出向量 = [
    [0.7*√3, 0.8*√3, 0.9*√3],  # 索引2
    [0.1*√3, 0.2*√3, 0.3*√3],  # 索引0
    [1.0*√3, 1.1*√3, 1.2*√3]   # 索引3
]

维度变化示意图

        输入形状                输出形状
       +-------+              +---------+
       | B x S |              | B x S x D|
       +-------+              +---------+
          |                        ^
          |       嵌入查找         |
          +----------------------->

常见问题解答

Q1：为什么要使用 sqrt(d_model) 进行缩放？
A1：主要出于两个考虑：

保持与位置编码的数值平衡：位置编码使用sin/cos函数生成，值域在[-1,1]之间
方差控制：假设嵌入值的初始方差为1，缩放后方差变为d_model，与后续层的预期输入范围匹配

Q2：如何处理不同长度的序列？
A2：通过padding机制：

短序列用0填充（如示例输入的最后一个位置）
实际应用中需要配合注意力掩码使用

Q3：嵌入层参数如何训练？
A3：训练过程：

前向传播时通过查表获取向量
反向传播时通过梯度下降更新嵌入矩阵
与Transformer其他参数联合优化

PositionalEncoding(位置编码实现)

import math
import torch
import torch.nn as nn


class PositionalEncoding(nn.Module):
    """
    Transformer 中的位置编码（Positional Encoding）实现

    █ 类的作用定位：
      - 上游：接收来自词嵌入层的输出张量
      - 下游：输出给多头注意力机制作为输入
      - 整体：为 Transformer 提供位置信息的核心组件，弥补其无序性缺陷

    █ 数学公式：
      PE(pos, 2i) = sin(pos / 10000^(2i/d_model))
      PE(pos, 2i+1) = cos(pos / 10000^(2i/d_model))
      其中：
      - pos 是 token 在序列中的位置索引
      - i 是维度索引
      - d_model 是嵌入向量的维度

    █ 初始化参数说明：
      | 参数名    | 类型   | 说明                          | 示例值 |
      |-----------|--------|-------------------------------|--------|
      | d_model   | int    | 嵌入向量维度                  | 512    |
      | dropout   | float  | Dropout比率                   | 0.1    |
      | max_len   | int    | 最大序列长度，默认为5000       | 5000   |
    """

    def __init__(self, d_model, dropout=0.1, max_len=5000):
        super(PositionalEncoding, self).__init__()
        
        # Dropout层对象：防止过拟合
        self.dropout = nn.Dropout(p=dropout)

        # 创建一个形状为 [max_len, d_model] 的零张量，用于存储位置编码
        pe = torch.zeros(max_len, d_model)

        # 创建一个形状为 [max_len, 1] 的张量，表示从 0 到 max_len-1 的位置索引
        position = torch.arange(0, max_len).unsqueeze(1)

        # 计算分母项 div_term，用于生成正弦和余弦波
        # div_term 的形状为 [d_model // 2]
        div_term = torch.exp(torch.arange(0, d_model, 2) * (-math.log(10000.0) / d_model))

        # 使用正弦函数计算偶数维度的位置编码
        pe[:, 0::2] = torch.sin(position * div_term)

        # 使用余弦函数计算奇数维度的位置编码
        pe[:, 1::2] = torch.cos(position * div_term)

        # 将位置编码张量扩展为形状 [1, max_len, d_model]，以便与批量数据兼容
        pe = pe.unsqueeze(0)

        # 注册位置编码张量为缓冲区，使其成为模型的一部分但不参与梯度更新
        self.register_buffer('pe', pe)

    def forward(self, x):
        """
        前向传播过程（维度变化图示）

        █ 输入输出规格：
          输入形状: [batch_size, sequence_length, d_model] 示例：[32, 50, 512]
          输出形状: [batch_size, sequence_length, d_model] 示例：[32, 50, 512]

        █ 处理步骤分解：
          原始输入（示例）：
          [[[ 0.1,  0.2, ...,  0.5],  # 第一个词的特征
            [-0.1, -0.2, ..., -0.5]], # 第二个词的特征
           [[ 1.0,  2.0, ...,  5.0],
            [-1.0, -2.0, ..., -5.0]]]

          步骤1：截取对应长度的位置编码
          self.pe[:, :x.size(1)] → 截取与输入序列长度相同的部分位置编码

          步骤2：将位置编码与输入张量相加
          x + self.pe[:, :x.size(1)]

          步骤3：应用 Dropout 操作
          output = self.dropout(x)
        """
        # Step 1: 将位置编码与输入张量相加
        x = x + self.pe[:, :x.size(1)]  # 仅使用与输入序列长度相同的部分位置编码

        # Step 2: 应用 Dropout 操作
        return self.dropout(x)

# 单元测试示例
if __name__ == "__main__":
    # 参数设置
    batch_size = 2
    seq_len = 3
    d_model = 4
    
    # 创建随机输入
    inputs = torch.randn(batch_size, seq_len, d_model)
    
    # 初始化位置编码层
    pos_enc = PositionalEncoding(d_model, dropout=0.1, max_len=5000)
    
    # 前向传播
    outputs = pos_enc(inputs)
    
    print("输入张量：")
    print(inputs)
    print("\n输出张量：")
    print(outputs)
    print("\n输出形状：", outputs.shape)

"""
预期输出示例：

输入张量：
tensor([[[ 0.1234, -0.5678,  1.2345, -2.3456],
         [-0.9876,  1.2345, -0.6789,  2.3456],
         [ 0.4321, -1.2345,  0.6789, -1.2345]],

        [[-0.5432,  1.2345, -0.9876,  0.4321],
         [ 0.6789, -1.2345,  0.4321, -0.9876],
         [-0.1234,  0.5678, -1.2345,  2.3456]]])

输出张量：
tensor([[[ 0.2345, -0.6789,  1.3456, -2.4567],
         [-1.0987,  1.3456, -0.7890,  2.4567],
         [ 0.5432, -1.3456,  0.7890, -1.3456]],

        [[-0.6543,  1.3456, -1.0987,  0.5432],
         [ 0.7890, -1.3456,  0.5432, -1.0987],
         [-0.2345,  0.6789, -1.3456,  2.4567]]])

输出形状： torch.Size([2, 3, 4])
"""

关键概念图解

位置编码工作流程

输入张量 (x) → 添加位置编码 → Dropout操作 → 输出张量
形状变化：[batch_size, seq_len, d_model] → [batch_size, seq_len, d_model]

维度变化可视化

# 假设输入为：
inputs = [
    [1.0, 2.0, 3.0, 4.0],  # 样本1的第一个词
    [5.0, 6.0, 7.0, 8.0]   # 样本2的第一个词
]

# Step 1: 截取对应长度的位置编码
positional_encoding = [
    [0.1, 0.2, 0.3, 0.4],  # 样本1的第一个词
    [0.5, 0.6, 0.7, 0.8]   # 样本2的第一个词
]

# Step 2: 相加操作
summed = [
    [1.1, 2.2, 3.3, 4.4],  # 样本1的第一个词
    [5.5, 6.6, 7.7, 8.8]   # 样本2的第一个词
]

# Step 3: Dropout操作
output = [
    [1.1, 2.2, 3.3, 4.4],  # 样本1的第一个词（部分值可能被置为0）
    [5.5, 6.6, 7.7, 8.8]   # 样本2的第一个词（部分值可能被置为0）
]

常见问题解答

Q1：为什么需要位置编码？
A1：Transformer模型没有像RNN或CNN那样的固有顺序性，因此需要显式地为每个token注入位置信息。位置编码通过正弦和余弦函数生成，能够捕捉相对位置关系。

Q2：正弦和余弦波的作用是什么？
A2：正弦和余弦波的作用是为不同维度的位置编码引入周期性变化，使得模型能够学习到相对位置信息，同时保持对长序列的有效表达能力。

Q3：为什么使用register_buffer？
A3：register_buffer用于注册非参数张量（如位置编码），使其成为模型的一部分但不参与梯度更新，从而节省计算资源并保持一致性。

subsequent_mask(生成掩码张量)

import torch
import numpy as np

def subsequent_mask(size):
    """
    生成一个后续掩码（subsequent mask），用于屏蔽未来的时间步信息。

    函数的作用:
    - 在 Transformer 的解码器中，为了确保在预测第 i 个位置的 token 时，模型只能看到当前位置及之前的 token，
      而不能看到未来的 token，需要使用后续掩码。
    - 该函数生成一个上三角矩阵，其中对角线及以下部分为 1，表示可以关注的位置；
      上三角部分为 0，表示需要屏蔽的位置。

    参数:
    - size: 掩码的大小，表示序列的长度。

    返回:
    - 返回一个形状为 [1, size, size] 的张量，类型为 uint8。
      - 1 表示可以关注的位置。
      - 0 表示需要屏蔽的位置。

    示例:
    subsequent_mask(size)
    如果 size=4，则生成的掩码为：
    [[[[1, 0, 0, 0],
       [1, 1, 0, 0],
       [1, 1, 1, 0],
       [1, 1, 1, 1]]]]
    """

    # 定义掩码的形状为 (1, size, size)，其中 1 表示批量维度。
    attn_shape = (1, size, size)

    # 使用 numpy 的 triu 函数生成上三角矩阵。
    # np.ones(attn_shape) 创建一个全 1 的矩阵，k=1 表示从主对角线上方第一行开始置 0。
    subsequent_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')

    # 将生成的上三角矩阵取反（1 变为 0，0 变为 1），并转换为 PyTorch 张量。
    return torch.from_numpy(1 - subsequent_mask)

Attention(注意力机制实现)

import copy
import math
import torch
import torch.nn as nn


def attention(query, key, value, mask=None, dropout=None):
    """
    计算注意力分数和加权求和的值。

    参数:
        query (torch.Tensor): 查询张量，形状为 [batch_size, num_heads, sequence_length, d_k]。
        key (torch.Tensor): 键张量，形状为 [batch_size, num_heads, sequence_length, d_k]。
        value (torch.Tensor): 值张量，形状为 [batch_size, num_heads, sequence_length, d_k]。
        mask (torch.Tensor, optional): 掩码张量，形状为 [batch_size, 1, sequence_length, sequence_length]。
        dropout (nn.Dropout, optional): Dropout 层对象。

    返回:
        output (torch.Tensor): 注意力加权求和后的输出，形状为 [batch_size, num_heads, sequence_length, d_k]。
        p_attn (torch.Tensor): 注意力权重，形状为 [batch_size, num_heads, sequence_length, sequence_length]。
    """
    d_k = query.size(-1)  # 获取每个头的维度 d_k

    # Step 1: 计算注意力分数
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
    # 矩阵乘法：计算查询和键的点积，并除以 sqrt(d_k) 进行缩放

    # Step 2: 应用掩码（如果存在）
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
        # 将掩码中为 0 的位置对应的分数设置为 -1e9，使得 softmax 后这些位置的概率接近于 0

    # Step 3: 计算注意力权重
    p_attn = torch.softmax(scores, dim=-1)
    # 沿最后一个维度进行 softmax 归一化，得到注意力权重

    # Step 4: 应用 Dropout（如果存在）
    if dropout is not None:
        p_attn = dropout(p_attn)

    # Step 5: 使用注意力权重加权求和值张量
    return torch.matmul(p_attn, value), p_attn


def clones(module, N):
    """
    克隆 N 个相同的模块。

    参数:
        module (nn.Module): 要克隆的模块。
        N (int): 克隆的数量。

    返回:
        nn.ModuleList: 包含 N 个克隆模块的列表。
    """
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])


class MultiHeadedAttention(nn.Module):
    """
    多头注意力机制实现。

    类的作用:
    - 在 Transformer 模型中，多头注意力是编码器和解码器子层中的核心组件。
    - 它通过将输入分解为多个头，分别计算注意力，然后合并结果，从而增强模型的表达能力。

    参数:
        head (int): 注意力头的数量。
        embedding_dim (int): 输入嵌入的维度。
        dropout (float, optional): Dropout 比率，默认为 0.1。

    属性:
        d_k (int): 每个头的维度。
        head (int): 注意力头的数量。
        embedding_dim (int): 输入嵌入的维度。
        linears (nn.ModuleList): 包含 4 个线性变换层的列表，分别用于查询、键、值和最终输出。
        attn (torch.Tensor): 存储注意力权重。
        dropout (nn.Dropout): Dropout 层对象。
    """

    def __init__(self, head, embedding_dim, dropout=0.1):
        super(MultiHeadedAttention, self).__init__()

        assert embedding_dim % head == 0, "embedding_dim 必须能被 head 整除"

        self.d_k = embedding_dim // head  # 每个头的维度
        self.head = head  # 注意力头的数量
        self.embedding_dim = embedding_dim  # 输入嵌入的维度

        # 克隆 4 个线性变换层，分别用于查询、键、值和最终输出
        self.linears = clones(nn.Linear(embedding_dim, embedding_dim), 4)

        self.attn = None  # 用于存储注意力权重
        self.dropout = nn.Dropout(p=dropout)  # Dropout 层对象

    def forward(self, query, key, value, mask=None):
        """
        前向传播逻辑。

        参数:
            query (torch.Tensor): 查询张量，形状为 [batch_size, sequence_length, embedding_dim]。
            key (torch.Tensor): 键张量，形状为 [batch_size, sequence_length, embedding_dim]。
            value (torch.Tensor): 值张量，形状为 [batch_size, sequence_length, embedding_dim]。
            mask (torch.Tensor, optional): 掩码张量，形状为 [batch_size, 1, sequence_length, sequence_length]。

        返回:
            torch.Tensor: 多头注意力机制的输出，形状为 [batch_size, sequence_length, embedding_dim]。
        """
        if mask is not None:
            mask = mask.unsqueeze(1)  # 调整掩码形状以适配多头注意力

        batch_size = query.size(0)  # 获取批量大小

        # Step 1: 使用线性变换层分别处理查询、键和值张量，并按头分割
        query, key, value = [
            model(x).view(batch_size, -1, self.head, self.d_k).transpose(1, 2)
            for model, x in zip(self.linears, (query, key, value))
        ]

        # Step 2: 调用 attention 函数计算多头注意力
        x, self.attn = attention(query, key, value, mask=mask, dropout=self.dropout)

        # Step 3: 将多头注意力的结果合并
        x = x.transpose(1, 2).contiguous().view(batch_size, -1, self.head * self.d_k)

        # Step 4: 通过最后一个线性变换层得到最终输出
        return self.linears[-1](x)

# 单元测试示例
if __name__ == "__main__":
    # 参数设置
    batch_size = 2
    seq_len = 3
    embedding_dim = 4
    heads = 2

    # 创建随机输入
    query = torch.randn(batch_size, seq_len, embedding_dim)
    key = torch.randn(batch_size, seq_len, embedding_dim)
    value = torch.randn(batch_size, seq_len, embedding_dim)

    # 初始化多头注意力层
    multihead_attn = MultiHeadedAttention(head=heads, embedding_dim=embedding_dim, dropout=0.1)

    # 前向传播
    output = multihead_attn(query, key, value)

    print("输入张量（Query）：")
    print(query)
    print("\n输出张量：")
    print(output)
    print("\n输出形状：", output.shape)

"""
预期输出示例：

输入张量（Query）：
tensor([[[ 0.1234, -0.5678,  1.2345, -2.3456],
         [-0.9876,  1.2345, -0.6789,  2.3456],
         [ 0.4321, -1.2345,  0.6789, -1.2345]],

        [[-0.5432,  1.2345, -0.9876,  0.4321],
         [ 0.6789, -1.2345,  0.4321, -0.9876],
         [-0.1234,  0.5678, -1.2345,  2.3456]]])

输出张量：
tensor([[[ 0.2345, -0.6789,  1.3456, -2.4567],
         [-1.0987,  1.3456, -0.7890,  2.4567],
         [ 0.5432, -1.3456,  0.7890, -1.3456]],

        [[-0.6543,  1.3456, -1.0987,  0.5432],
         [ 0.7890, -1.3456,  0.5432, -1.0987],
         [-0.2345,  0.6789, -1.3456,  2.4567]]])

输出形状： torch.Size([2, 3, 4])
"""

关键概念图解

多头注意力工作流程

输入张量 (Query, Key, Value) → 线性变换 → 分割为多头 → 计算注意力 → 合并多头 → 最终线性变换 → 输出张量
形状变化：
Query/Key/Value: [batch_size, sequence_length, embedding_dim]
→ 线性变换后: [batch_size, sequence_length, embedding_dim]
→ 分割为多头后: [batch_size, num_heads, sequence_length, d_k]
→ 注意力计算后: [batch_size, num_heads, sequence_length, d_k]
→ 合并多头后: [batch_size, sequence_length, embedding_dim]
→ 最终线性变换后: [batch_size, sequence_length, embedding_dim]

维度变化可视化

# 假设输入为：
query = [
    [[1.0, 2.0, 3.0, 4.0], [5.0, 6.0, 7.0, 8.0]],  # 样本1
    [[9.0, 10.0, 11.0, 12.0], [13.0, 14.0, 15.0, 16.0]]  # 样本2
]

# Step 1: 线性变换
linear_query = [
    [[1.1, 2.2, 3.3, 4.4], [5.5, 6.6, 7.7, 8.8]],  # 样本1
    [[9.9, 10.1, 11.1, 12.1], [13.1, 14.1, 15.1, 16.1]]  # 样本2
]

# Step 2: 分割为多头
split_query = [
    [[[1.1, 2.2], [3.3, 4.4]], [[5.5, 6.6], [7.7, 8.8]]],  # 样本1
    [[[9.9, 10.1], [11.1, 12.1]], [[13.1, 14.1], [15.1, 16.1]]]  # 样本2
]

# Step 3: 注意力计算
attention_output = [
    [[[1.2, 2.3], [3.4, 4.5]], [[5.6, 6.7], [7.8, 8.9]]],  # 样本1
    [[[9.0, 10.0], [11.0, 12.0]], [[13.0, 14.0], [15.0, 16.0]]]  # 样本2
]

# Step 4: 合并多头
merged_output = [
    [[1.2, 2.3, 3.4, 4.5], [5.6, 6.7, 7.8, 8.9]],  # 样本1
    [[9.0, 10.0, 11.0, 12.0], [13.0, 14.0, 15.0, 16.0]]  # 样本2
]

# Step 5: 最终线性变换
final_output = [
    [[1.3, 2.4, 3.5, 4.6], [5.7, 6.8, 7.9, 8.0]],  # 样本1
    [[9.1, 10.2, 11.3, 12.4], [13.5, 14.6, 15.7, 16.8]]  # 样本2
]

常见问题解答

Q1：为什么需要多头注意力？
A1：多头注意力通过将输入分解为多个头，分别计算注意力，然后合并结果，增强了模型的表达能力。每个头可以关注输入的不同部分，从而捕捉到更丰富的信息。

Q2：softmax在注意力机制中的作用是什么？
A2：softmax将注意力分数归一化为概率分布，使得每个位置的权重都在 [0, 1] 范围内，且所有位置的权重之和为 1。这有助于模型根据重要性分配权重。

Q3：dropout在多头注意力中的作用是什么？
A3：dropout通过随机抑制部分注意力权重，防止过拟合，提高模型的泛化能力。

PositionwiseFeedForward(前馈层实现)

import torch.nn as nn
import torch.nn.functional as F


class PositionwiseFeedForward(nn.Module):
    """
    Transformer 中的位置前馈网络（Position-wise Feed-Forward Network）

    █ 类的作用定位：
      - 上游：接收来自多头注意力层的输出张量
      - 下游：输出给残差连接，与输入相加形成最终输出
      - 整体：增强模型表达能力的核心组件之一，通过非线性变换捕捉复杂模式

    █ 数学公式：
      FFN(x) = W_2 * ReLU(W_1 * x + b_1) + b_2
      其中：
      - W_1, b_1 是第一个线性变换的权重和偏置
      - W_2, b_2 是第二个线性变换的权重和偏置

    █ 初始化参数说明：
      | 参数名    | 类型   | 说明                          | 示例值 |
      |-----------|--------|-------------------------------|--------|
      | d_model   | int    | 输入嵌入维度                  | 512    |
      | d_ff      | int    | 隐藏层维度（通常是d_model的4倍） | 2048   |
      | dropout   | float  | Dropout比率                   | 0.1    |
    """

    def __init__(self, d_model, d_ff, dropout=0.1):
        super(PositionwiseFeedForward, self).__init__()
        
        # 第一个线性变换层：将输入从d_model映射到d_ff
        self.w_1 = nn.Linear(d_model, d_ff)
        
        # 第二个线性变换层：将隐藏层从d_ff映射回d_model
        self.w_2 = nn.Linear(d_ff, d_model)
        
        # Dropout层对象：防止过拟合
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        """
        前向传播过程（维度变化图示）
        
        █ 输入输出规格：
          输入形状: [batch_size, sequence_length, d_model] 示例：[32, 50, 512]
          输出形状: [batch_size, sequence_length, d_model] 示例：[32, 50, 512]
        
        █ 处理步骤分解：
          原始输入（示例）：
          [[[ 0.1,  0.2, ...,  0.5],  # 第一个词的特征
            [-0.1, -0.2, ..., -0.5]], # 第二个词的特征
           [[ 1.0,  2.0, ...,  5.0],
            [-1.0, -2.0, ..., -5.0]]]

          步骤1：第一个线性变换 w_1
          将输入从d_model维度映射到d_ff维度
          hidden = w_1(x)

          步骤2：ReLU激活函数
          引入非线性，使模型能够学习复杂的模式
          activated = ReLU(hidden)

          步骤3：Dropout操作
          随机将部分神经元置为0，防止过拟合
          dropped = Dropout(activated)

          步骤4：第二个线性变换 w_2
          将隐藏层从d_ff维度映射回d_model维度
          output = w_2(dropped)
        """
        # Step 1: 第一个线性变换层
        hidden = self.w_1(x)  # 形状变为 [batch_size, sequence_length, d_ff]

        # Step 2: 应用 ReLU 激活函数
        activated = F.relu(hidden)  # 形状保持不变 [batch_size, sequence_length, d_ff]

        # Step 3: 应用 Dropout 操作
        dropped = self.dropout(activated)  # 形状保持不变 [batch_size, sequence_length, d_ff]

        # Step 4: 第二个线性变换层
        output = self.w_2(dropped)  # 形状变回 [batch_size, sequence_length, d_model]

        return output

# 单元测试示例
if __name__ == "__main__":
    # 参数设置
    batch_size = 2
    seq_len = 3
    d_model = 4
    d_ff = 8
    
    # 创建随机输入
    inputs = torch.randn(batch_size, seq_len, d_model)
    
    # 初始化位置前馈网络
    ffn = PositionwiseFeedForward(d_model, d_ff, dropout=0.1)
    
    # 前向传播
    outputs = ffn(inputs)
    
    print("输入张量：")
    print(inputs)
    print("\n输出张量：")
    print(outputs)
    print("\n输出形状：", outputs.shape)

"""
预期输出示例：

输入张量：
tensor([[[ 0.1234, -0.5678,  1.2345, -2.3456],
         [-0.9876,  1.2345, -0.6789,  2.3456],
         [ 0.4321, -1.2345,  0.6789, -1.2345]],

        [[-0.5432,  1.2345, -0.9876,  0.4321],
         [ 0.6789, -1.2345,  0.4321, -0.9876],
         [-0.1234,  0.5678, -1.2345,  2.3456]]])

输出张量：
tensor([[[ 0.7890, -1.2345,  1.5678, -2.3456],
         [-1.4567,  1.8901, -0.7890,  2.5678],
         [ 0.1234, -1.5678,  0.4567, -1.2345]],

        [[-0.6789,  1.4567, -1.2345,  0.5678],
         [ 0.7890, -1.4567,  0.5678, -1.2345],
         [-0.2345,  0.8901, -1.5678,  2.3456]]])

输出形状： torch.Size([2, 3, 4])
"""

关键概念图解

位置前馈网络工作流程

输入张量 (x) → 线性变换 (W_1) → ReLU激活 → Dropout → 线性变换 (W_2) → 输出张量
形状变化：[batch_size, seq_len, d_model] → [batch_size, seq_len, d_ff] → [batch_size, seq_len, d_model]

维度变化可视化

# 假设输入为：
inputs = [
    [1.0, 2.0, 3.0, 4.0],  # 样本1的第一个词
    [5.0, 6.0, 7.0, 8.0]   # 样本2的第一个词
]

# Step 1: 第一线性变换 W_1
hidden = [OSS
    [0.1, 0.2, ..., 0.8],  # 样本1的第一个词
    [0.5, 0.6, ..., 1.2]   # 样本2的第一个词
]

# Step 2: ReLU激活
activated = [
    [0.1, 0.2, ..., 0.8],  # 样本1的第一个词
    [0.5, 0.6, ..., 1.2]   # 样本2的第一个词
]

# Step 3: Dropout
dropped = [
    [0.0, 0.2, ..., 0.8],  # 样本1的第一个词（部分值被置为0）
    [0.5, 0.0, ..., 1.2]   # 样本2的第一个词（部分值被置为0）
]

# Step 4: 第二线性变换 W_2
output = [
    [1.1, 2.2, 3.3, 4.4],  # 样本1的第一个词
    [5.5, 6.6, 7.7, 8.8]   # 样本2的第一个词
]

常见问题解答

Q1：为什么需要两个线性变换？
A1：两个线性变换的作用分别是：

扩展维度：通过第一个线性变换将输入映射到更高维度（d_ff），增加模型的表达能力。
压缩维度：通过第二个线性变换将隐藏层映射回原始维度（d_model），保持与输入一致。

Q2：ReLU的作用是什么？
A2：ReLU是一种非线性激活函数，定义为 $\max(0, x)$ 。它的作用是引入非线性，使模型能够学习复杂的模式。

Q3：Dropout的作用是什么？
A3：Dropout是一种正则化方法，随机将部分神经元的输出置为0，从而防止过拟合，提高模型的泛化能力。

LayerNorm(层归一化实现)

import torch
import torch.nn as nn


class LayerNorm(nn.Module):
    """
    Transformer 中的层归一化（Layer Normalization）实现
    
    █ 类的作用定位：
      - 上游：接收来自前一层（如多头注意力或前馈网络）的输出
      - 下游：输出给残差连接，与输入相加形成最终输出
      - 整体：稳定神经网络隐藏状态分布的核心组件，加速训练并提高模型性能
    
    █ 数学公式：
      LN(x) = a_2 * (x - mean) / (std + eps) + b_2
      其中：
      - mean = E[x] 是最后一个维度的均值
      - std = sqrt(Var[x] + eps) 是标准差
      - a_2, b_2 是可学习参数
    
    █ 初始化参数说明：
      | 参数名    | 类型   | 说明                          | 示例值 |
      |-----------|--------|-------------------------------|--------|
      | features  | int    | 输入张量最后一个维度的大小     | 512    |
      | eps       | float  | 防止除零的小常数              | 1e-6   |
    """

    def __init__(self, features, eps=1e-6):
        super(LayerNorm, self).__init__()
        
        # 可学习参数初始化
        self.a_2 = nn.Parameter(torch.ones(features))  # 缩放参数
        self.b_2 = nn.Parameter(torch.zeros(features)) # 偏移参数
        self.eps = eps                                # 数值稳定性常数

    def forward(self, x):
        """
        前向传播过程（维度变化图示）
        
        █ 输入输出规格：
          输入形状: [batch_size, sequence_length, features] 示例：[32, 50, 512]
          输出形状: [batch_size, sequence_length, features] 示例：[32, 50, 512]
        
        █ 处理步骤分解：
          原始输入（示例）：
          [[[ 0.1,  0.2,  0.3],  # 第一个词的特征
            [-0.1, -0.2, -0.3]], # 第二个词的特征
           [[ 1.0,  2.0,  3.0],
            [-1.0, -2.0, -3.0]]]
          
          步骤1：计算均值和标准差
          mean = [[ 0.0,  0.0,  0.0], 
                  [ 0.0,  0.0,  0.0]]
          std  = [[ 0.1414,  0.2828,  0.4243],
                  [ 1.4142,  2.8284,  4.2426]]
          
          步骤2：标准化处理
          normalized = [[[ 0.7071,  0.7071,  0.7071],
                         [-0.7071, -0.7071, -0.7071]],
                        [[ 0.7071,  0.7071,  0.7071],
                         [-0.7071, -0.7071, -0.7071]]]
          
          步骤3：应用可学习参数
          output = a_2 * normalized + b_2
        """
        # 计算统计量
        mean = x.mean(-1, keepdim=True)  # 沿最后一个维度计算均值
        std = x.std(-1, keepdim=True)    # 沿最后一个维度计算标准差
        
        # 归一化处理
        normalized_x = (x - mean) / (std + self.eps)
        
        # 应用可学习参数
        return self.a_2 * normalized_x + self.b_2

# 单元测试示例
if __name__ == "__main__":
    # 参数设置
    batch_size = 2
    seq_len = 3
    feature_dim = 4
    
    # 创建随机输入
    inputs = torch.randn(batch_size, seq_len, feature_dim)
    
    # 初始化LayerNorm层
    layer_norm = LayerNorm(feature_dim)
    
    # 前向传播
    outputs = layer_norm(inputs)
    
    print("输入张量：")
    print(inputs)
    print("\n输出张量：")
    print(outputs)
    print("\n输出形状：", outputs.shape)

"""
预期输出示例：

输入张量：
tensor([[[ 0.1234, -0.5678,  1.2345, -2.3456],
         [-0.9876,  1.2345, -0.6789,  2.3456],
         [ 0.4321, -1.2345,  0.6789, -1.2345]],

        [[-0.5432,  1.2345, -0.9876,  0.4321],
         [ 0.6789, -1.2345,  0.4321, -0.9876],
         [-0.1234,  0.5678, -1.2345,  2.3456]]])

输出张量：
tensor([[[ 0.7890, -1.2345,  1.5678, -2.3456],
         [-1.4567,  1.8901, -0.7890,  2.5678],
         [ 0.1234, -1.5678,  0.4567, -1.2345]],

        [[-0.6789,  1.4567, -1.2345,  0.5678],
         [ 0.7890, -1.4567,  0.5678, -1.2345],
         [-0.2345,  0.8901, -1.5678,  2.3456]]])

输出形状： torch.Size([2, 3, 4])
"""

关键概念图解

层归一化 vs 批归一化

BatchNorm:
- 统计量在batch维度计算
- 对整个mini-batch进行归一化
- 不适合序列数据和小batch场景

LayerNorm:
- 统计量在feature维度计算
- 对每个样本独立归一化
- 更适合NLP任务和变长序列

归一化过程可视化

# 假设输入为：
inputs = [
    [1.0, 2.0, 3.0],  # 样本1
    [4.0, 5.0, 6.0]   # 样本2
]

# 计算统计量
mean = [2.0, 5.0]     # 每行均值
std  = [0.8165, 0.8165] # 每行标准差

# 归一化结果
normalized = [
    [-1.2247,  0.0000,  1.2247],  # 样本1
    [-1.2247,  0.0000,  1.2247]   # 样本2
]

# 应用可学习参数
output = a_2 * normalized + b_2

常见问题解答

Q1：为什么使用可学习参数a_2和b_2？
A1：两个主要原因：

提供额外的灵活性：允许模型根据任务需求调整归一化后的分布
恢复表达能力：防止归一化操作丢失重要特征信息

Q2：eps的作用是什么？
A2：主要作用：

数值稳定性：防止标准差为0导致除零错误
平滑效果：避免极端值对归一化的影响

Q3：如何与残差连接配合使用？
A3：典型结构：

sublayer_output = sublayer(layer_norm(x))
final_output = x + dropout(sublayer_output)

这种结构既保留了原始信息，又引入了归一化后的变换结果

SubLayerConnection(子层连接结构实现)

import torch.nn as nn

class SubLayerConnection(nn.Module):
    """
    Transformer 中的子层连接（Sublayer Connection）实现
    
    █ 类的作用定位：
      - 上游：接收来自多头注意力或前馈网络子层的输出
      - 下游：输出给下一个子层或模型最终输出
      - 整体：通过残差连接和层归一化，增强模型稳定性并加速收敛
      
    █ 数学公式：
      Output = x + Dropout(Sublayer(LayerNorm(x)))
      
    █ 初始化参数说明：
      | 参数名   | 类型   | 说明                          | 示例值 |
      |----------|--------|-------------------------------|--------|
      | size     | int    | 输入张量最后一个维度的大小     | 512    |
      | dropout  | float  | Dropout比率                   | 0.1    |
    """

    def __init__(self, size, dropout):
        super(SubLayerConnection, self).__init__()
        
        # 层归一化对象：对输入张量进行归一化处理
        self.norm = nn.LayerNorm(size)
        
        # Dropout对象：随机抑制部分神经元输出，防止过拟合
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):
        """
        前向传播过程（维度变化图示）
        
        █ 输入输出规格：
          输入形状: [batch_size, sequence_length, size] 示例：[32, 50, 512]
          输出形状: [batch_size, sequence_length, size] 示例：[32, 50, 512]
        
        █ 处理步骤分解：
          原始输入（示例）：
          [[[ 0.1,  0.2, ...,  0.5],  # 第一个词的特征
            [-0.1, -0.2, ..., -0.5]], # 第二个词的特征
           [[ 1.0,  2.0, ...,  5.0],
            [-1.0, -2.0, ..., -5.0]]]

          步骤1：层归一化
          normalized_x = LayerNorm(x)

          步骤2：子层处理
          sublayer_output = sublayer(normalized_x)

          步骤3：Dropout操作
          dropped_output = Dropout(sublayer_output)

          步骤4：残差连接
          output = x + dropped_output
        """
        # Step 1: 对输入张量进行层归一化
        normalized_x = self.norm(x)  # 形状保持不变 [batch_size, sequence_length, size]

        # Step 2: 将归一化后的结果传入子层处理
        sublayer_output = sublayer(normalized_x)  # 子层输出形状与输入相同 [batch_size, sequence_length, size]

        # Step 3: 对子层输出应用 Dropout 操作
        dropped_output = self.dropout(sublayer_output)  # 形状保持不变 [batch_size, sequence_length, size]

        # Step 4: 添加残差连接
        return x + dropped_output  # 形状保持不变 [batch_size, sequence_length, size]

# 单元测试示例 
if __name__ == "__main__":
    # 参数设置
    batch_size = 2
    seq_len = 3
    d_model = 4
    dropout_rate = 0.1
    
    # 创建随机输入
    inputs = torch.randn(batch_size, seq_len, d_model)
    
    # 定义子层函数（例如一个简单的线性变换）
    def dummy_sublayer(x):
        linear = nn.Linear(d_model, d_model)
        return linear(x)
    
    # 初始化子层连接
    sublayer_conn = SubLayerConnection(d_model, dropout_rate)
    
    # 前向传播
    outputs = sublayer_conn(inputs, dummy_sublayer)
    
    print("输入张量：")
    print(inputs)
    print("\n输出张量：")
    print(outputs)
    print("\n输出形状：", outputs.shape)

"""
预期输出示例：

输入张量：
tensor([[[ 0.1234, -0.5678,  1.2345, -2.3456],
         [-0.9876,  1.2345, -0.6789,  2.3456],
         [ 0.4321, -1.2345,  0.6789, -1.2345]],

        [[-0.5432,  1.2345, -0.9876,  0.4321],
         [ 0.6789, -1.2345,  0.4321, -0.9876],
         [-0.1234,  0.5678, -1.2345,  2.3456]]])

输出张量：
tensor([[[ 0.2345, -0.6789,  1.3456, -2.4567],
         [-1.0987,  1.3456, -0.7890,  2.4567],
         [ 0.5432, -1.3456,  0.7890, -1.3456]],

        [[-0.6543,  1.3456, -1.0987,  0.5432],
         [ 0.7890, -1.3456,  0.5432, -1.0987],
         [-0.2345,  0.6789, -1.3456,  2.4567]]])

输出形状： torch.Size([2, 3, 4])
"""

关键概念图解

子层连接工作流程

输入张量 (x) → 层归一化 → 子层处理 → Dropout操作 → 残差连接 → 输出张量
形状变化：[batch_size, seq_len, d_model] → [batch_size, seq_len, d_model]

维度变化可视化

# 假设输入为：
inputs = [
    [1.0, 2.0, 3.0, 4.0],  # 样本1的第一个词
    [5.0, 6.0, 7.0, 8.0]   # 样本2的第一个词
]

# Step 1: 层归一化
normalized = [
    [0.1, 0.2, 0.3, 0.4],  # 样本1的第一个词
    [0.5, 0.6, 0.7, 0.8]   # 样本2的第一个词
]

# Step 2: 子层处理
sublayer_output = [
    [0.2, 0.3, 0.4, 0.5],  # 样本1的第一个词
    [0.6, 0.7, 0.8, 0.9]   # 样本2的第一个词
]

# Step 3: Dropout操作
dropped_output = [
    [0.2, 0.0, 0.4, 0.5],  # 样本1的第一个词（部分值被置为0）
    [0.6, 0.7, 0.0, 0.9]   # 样本2的第一个词（部分值被置为0）
]

# Step 4: 残差连接
output = [
    [1.2, 2.0, 3.4, 4.5],  # 样本1的第一个词
    [5.6, 6.7, 7.0, 8.9]   # 样本2的第一个词
]

常见问题解答

Q1：为什么需要残差连接？
A1：残差连接的主要作用是缓解深层网络中的梯度消失问题，使训练更加稳定。它通过将输入直接加到输出上，保留了原始信息，帮助模型更容易学习恒等映射。

Q2：层归一化的意义是什么？
A2：层归一化通过调整每个样本的分布，使其均值为0、方差为1，从而稳定训练过程。此外，可学习参数a2和b2允许模型灵活调整归一化后的分布。

Q3：Dropout的作用是什么？
A3：Dropout是一种正则化方法，通过随机抑制部分神经元的输出，防止模型过拟合。这有助于提高模型的泛化能力。

EncoderLayer(编码器层实现)

import torch.nn as nn
from transformer_test.attention import clones
from transformer_test.sub_layer_connection import SubLayerConnection


class EncoderLayer(nn.Module):
    """
    Transformer 编码器层模块

    功能描述：
        本类实现了Transformer编码器的一个基础层，包含以下核心组件：
        - 多头自注意力机制（处理序列内部依赖关系）
        - 前馈神经网络（特征非线性变换）
        - 残差连接（缓解梯度消失）
        - 层归一化（稳定训练过程）

    架构位置：
        - 上游模块：嵌入层（Embedding）或前一个编码器层
        - 下游模块：下一个编码器层或解码器层
        在整个Transformer架构中，多个EncoderLayer堆叠构成完整的编码器，
        负责将输入序列转换为高层次的语义表示。

    设计要点：
        每个子层（自注意力/前馈网络）的输出均采用 LayerNorm(x + Sublayer(x)) 结构，
        这种残差连接设计允许模型学习输入数据的增量调整。
    """

    def __init__(self, size, self_attn, feed_forward, dropout):
        """
        初始化编码器层
        
        参数说明：
            size (int):         特征维度（即d_model，通常为512）
            self_attn (nn.Module): 多头自注意力模块实例
            feed_forward (nn.Module): 前馈神经网络模块实例
            dropout (float):     dropout概率值
        """
        super(EncoderLayer, self).__init__()
        self.self_attn = self_attn       # 多头自注意力子层
        self.feed_forward = feed_forward # 前馈神经网络子层
        self.size = size                 # 特征维度
        # 创建两个SubLayerConnection实例（分别对应自注意力和前馈网络）
        self.layers = clones(SubLayerConnection(size, dropout), 2)

    def forward(self, x, mask):
        """
        前向传播过程

        输入参数：
            x (torch.Tensor): 输入序列张量，形状为 (batch_size, seq_len, d_model)
            mask (torch.Tensor): 注意力掩码张量，形状为 (batch_size, 1, seq_len) 或 (batch_size, seq_len, seq_len)

        输出说明：
            torch.Tensor: 处理后的序列张量，形状保持 (batch_size, seq_len, d_model)

        计算步骤详解：
            1. 第一子层处理（自注意力）：
               a. 执行层归一化
               b. 计算自注意力
               c. 应用dropout
               d. 残差连接（输入x + 处理结果）
            2. 第二子层处理（前馈网络）：
               a. 执行层归一化
               b. 前馈网络计算
               c. 应用dropout
               d. 残差连接
        """
        # 处理自注意力子层（lambda定义传递给SubLayerConnection的函数）
        x = self.layers[0](x, lambda x: self.self_attn(x, x, x, mask))
        # 处理前馈网络子层（注意此处无需mask）
        return self.layers[1](x, self.feed_forward)


########################################
# 示例代码与可视化（假设其他模块已实现）
########################################

if __name__ == "__main__":
    # 示例参数
    d_model = 512     # 特征维度
    seq_len = 10      # 序列长度
    batch_size = 2    # 批大小
    dropout_rate = 0.1

    # 假设已实现的模块（仅用于演示）
    from transformer_test.attention import MultiHeadedAttention
    from transformer_test.feed_forward import PositionwiseFeedForward

    # 初始化组件
    attn = MultiHeadedAttention(8, d_model)  # 8头注意力
    ff = PositionwiseFeedForward(d_model, 2048, dropout_rate)
    encoder_layer = EncoderLayer(d_model, attn, ff, dropout_rate)

    # 生成测试输入（随机初始化）
    test_input = torch.randn(batch_size, seq_len, d_model)
    test_mask = torch.ones(batch_size, 1, seq_len)  # 假设全1掩码

    # 前向传播
    output = encoder_layer(test_input, test_mask)

    # 打印形状验证
    print("输入形状:", test_input.shape)   # 预期输出: torch.Size([2, 10, 512])
    print("输出形状:", output.shape)      # 预期输出: torch.Size([2, 10, 512])

    """
    典型输出示例：
    输入形状: torch.Size([2, 10, 512])
    输出形状: torch.Size([2, 10, 512])

    中间数据流变化示意：
    输入张量 → [自注意力处理] → 中间表示 → [前馈网络处理] → 最终输出
    （所有步骤保持维度一致）
    """

关键组件详解

1. SubLayerConnection 的作用

# 伪代码示意
class SubLayerConnection(nn.Module):
    def __init__(self, size, dropout):
        super().__init__()
        self.norm = LayerNorm(size)   # 层归一化
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):
        """
        执行步骤：
        1. 对输入x进行层归一化 → norm(x)
        2. 应用子层函数（自注意力或前馈网络） → sublayer(norm(x))
        3. 对结果进行dropout → dropout(sublayer_out)
        4. 残差连接 → x + dropout_out
        """
        return x + self.dropout(sublayer(self.norm(x)))

2. 维度变化流程

步骤	操作	维度变化
输入	-	(2, 10, 512)
自注意力子层	多头注意力计算	(2, 10, 512) → (2, 10, 512)
前馈子层	线性变换+激活	(2, 10, 512) → (2, 10, 512)

3. 关键PyTorch函数

nn.Dropout: 以概率dropout随机将输入张量的元素置零，防止过拟合
LayerNorm: 沿特征维度（最后一维）进行归一化计算，公式：
[
\text{输出} = \frac{x - \mu}{\sigma} \cdot \gamma + \beta
]
其中γ、β为可学习参数

4. 自注意力机制特点

计算序列内部各位置间的相关性
使用掩码防止关注到无效位置（如填充位置）
多头设计允许模型关注不同子空间的信息

扩展理解

残差连接的意义：允许梯度直接流过整个网络，缓解深层网络的梯度消失问题
层归一化的优势：对比批量归一化，更适合处理变长序列数据
编码器堆叠效果：多层编码器的逐层处理使得高层可以捕捉更复杂的语义特征

通过这种设计，每个编码器层能够有效提取输入序列的层次化特征，为下游的解码器提供丰富的语义表示。

Encoder(解码器实现)

import torch.nn as nn

from transformer_test.attention import clones
from transformer_test.layer_norm import LayerNorm


class Encoder(nn.Module):
    def __init__(self, layer, N):
        """
        :param layer: 编码器层
        :param N: 编码器层的个数
        """
        super(Encoder, self).__init__()

        # clones 函数克隆N个编码器
        self.layers = clones(layer, N)
        # 初始化规范化层, 用在编码器最后
        self.norm = LayerNorm(layer.size)

    def forward(self, x, mask):
        """
        :param x: 输入
        :param mask: 屏蔽
        :return:
        """
        # 循环执行N个编码器
        for layer in self.layers:
            x = layer(x, mask)
        return self.norm(x)

DecoderLayer(编码器层实现)

import torch.nn as nn
from transformer_test.attention import clones
from transformer_test.sub_layer_connection import SubLayerConnection


class DecoderLayer(nn.Module):
    """
    Transformer 解码器层模块

    功能描述：
        实现Transformer解码器的基本单元，包含三个核心组件：
        - 掩码多头自注意力机制（处理目标序列位置间依赖）
        - 交叉注意力机制（对齐编码器输出与目标序列）
        - 前馈神经网络（特征非线性变换）
        每个子层采用残差连接和层归一化，结构为：LayerNorm(x + Sublayer(x))

    架构位置：
        - 上游模块：目标序列嵌入层或前一个解码器层
        - 下游模块：下一个解码器层或输出生成层
        在Transformer架构中，多个DecoderLayer堆叠构成完整解码器，负责逐步生成目标序列

    设计特点：
        1. 使用目标掩码（tgt_mask）防止未来信息泄露
        2. 通过交叉注意力整合编码器输出的语义信息
        3. 三阶段处理流程：自注意 → 交叉注意 → 特征增强
    """

    def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
        """
        初始化解码器层

        参数说明：
            size (int):         特征维度（d_model，通常为512）
            self_attn (nn.Module): 掩码多头自注意力模块
            src_attn (nn.Module): 交叉注意力模块（Q来自目标序列，K/V来自编码器）
            feed_forward (nn.Module): 前馈网络模块
            dropout (float):     dropout概率值
        """
        super(DecoderLayer, self).__init__()
        self.self_attn = self_attn     # 目标序列自注意力（带掩码）
        self.src_attn = src_attn       # 编码器-解码器交叉注意力
        self.feed_forward = feed_forward
        self.size = size
        # 创建3个子层连接（SubLayerConnection包含层归一化+残差连接）
        self.sublayer = clones(SubLayerConnection(size, dropout), 3)

    def forward(self, x, memory, src_mask, tgt_mask):
        """
        前向传播流程

        输入参数：
            x (torch.Tensor): 目标序列张量，形状为 (batch_size, tgt_seq_len, d_model)
            memory (torch.Tensor): 编码器输出张量，形状为 (batch_size, src_seq_len, d_model)
            src_mask (torch.Tensor): 源序列掩码，形状为 (batch_size, 1, src_seq_len)
            tgt_mask (torch.Tensor): 目标序列掩码，形状为 (batch_size, tgt_seq_len, tgt_seq_len)

        输出说明：
            torch.Tensor: 处理后的目标序列，形状保持 (batch_size, tgt_seq_len, d_model)

        计算流程：
            [阶段1] 掩码自注意力（处理目标序列内部关系）
                → 层归一化 → 多头自注意 → dropout → 残差连接
            [阶段2] 交叉注意力（对齐编码器输出）
                → 层归一化 → 多头交叉注意 → dropout → 残差连接 
            [阶段3] 前馈神经网络（特征增强）
                → 层归一化 → 全连接 → dropout → 残差连接
        """
        # 阶段1：带掩码的自注意力（防止看到未来信息）
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
        
        # 阶段2：编码器-解码器注意力（Q来自解码器，K/V来自编码器）
        x = self.sublayer[1](x, lambda x: self.src_attn(x, memory, memory, src_mask))
        
        # 阶段3：前馈网络（独立处理每个位置）
        return self.sublayer[2](x, self.feed_forward)


###########################################
# 代码示例与执行结果（假设其他模块已实现）
###########################################

if __name__ == "__main__":
    # 配置参数
    d_model = 512       # 特征维度
    tgt_len = 10        # 目标序列长度
    src_len = 20        # 源序列长度
    batch_size = 2      # 批大小
    dropout_rate = 0.1

    # 假设实现的组件（用于演示）
    from transformer_test.attention import MultiHeadedAttention
    from transformer_test.feed_forward import PositionwiseFeedForward

    # 初始化组件
    self_attn = MultiHeadedAttention(8, d_model)  # 8头自注意力
    src_attn = MultiHeadedAttention(8, d_model)   # 8头交叉注意力
    ff = PositionwiseFeedForward(d_model, 2048, dropout_rate)
    
    decoder_layer = DecoderLayer(d_model, self_attn, src_attn, ff, dropout_rate)

    # 生成测试数据
    x = torch.randn(batch_size, tgt_len, d_model)        # 目标序列输入
    memory = torch.randn(batch_size, src_len, d_model)   # 编码器输出
    src_mask = torch.ones(batch_size, 1, src_len)        # 源序列掩码
    tgt_mask = torch.tril(torch.ones(tgt_len, tgt_len))  # 下三角掩码矩阵

    # 前向传播
    output = decoder_layer(x, memory, src_mask, tgt_mask)

    # 打印维度验证
    print("输入x形状:", x.shape)          # torch.Size([2, 10, 512])
    print("编码输出形状:", memory.shape)   # torch.Size([2, 20, 512])
    print("输出形状:", output.shape)      # torch.Size([2, 10, 512])

    """
    典型执行结果：
    输入x形状: torch.Size([2, 10, 512])
    编码输出形状: torch.Size([2, 20, 512])
    输出形状: torch.Size([2, 10, 512])

    数据流变化示意：
    (目标序列) → [掩码自注意] → [交叉注意] → [前馈网络] → 增强后的目标表示
    整个过程中各层维度保持 (batch_size, seq_len, d_model) 不变
    """

关键组件详解

1. 子层连接机制（SubLayerConnection）

# 伪代码示例
class SubLayerConnection(nn.Module):
    def __init__(self, size, dropout):
        self.norm = LayerNorm(size)   # 层归一化
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer_fn):
        """
        执行步骤：
        1. 层归一化: norm(x) → (batch, seq, d_model)
        2. 应用子层函数: sublayer_fn(norm_x) → (batch, seq, d_model)
        3. Dropout: dropout(sublayer_out) → (batch, seq, d_model)
        4. 残差连接: x + dropout_out → (batch, seq, d_model)
        """
        return x + self.dropout(sublayer_fn(self.norm(x)))

2. 维度变化流程

处理阶段	操作	维度变化
输入x	-	(2,10,512)
自注意力	掩码多头注意力	(2,10,512) → (2,10,512)
交叉注意力	编码器对齐	(2,10,512) → (2,10,512)
前馈网络	特征非线性变换	(2,10,512) → (2,10,512)

3. 核心PyTorch组件

LayerNorm：沿特征维度归一化，消除层间协变量偏移

# 计算示例（特征维度为3）
input = torch.tensor([[1.0, 2.0, 3.0], 
                     [4.0, 5.0, 6.0]])
normalized = (input - input.mean(-1, keepdim=True)) / input.std(-1, keepdim=True)

nn.Dropout：随机置零部分神经元，增强泛化能力

# 输入为[[1,2], [3,4]]，p=0.5的可能输出
[[0, 4],  # 第一个元素被置零
 [6, 0]]  # 50%概率乘以2（1/(1-p)）

4. 注意力机制对比

类型	Q来源	K/V来源	作用
自注意力	目标序列	目标序列	捕捉目标内部依赖关系
交叉注意力	目标序列	编码器输出	对齐源-目标语义信息

扩展理解

掩码机制的双重作用
- 目标掩码（tgt_mask）：防止解码器看到未来信息，保证自回归特性
- 源掩码（src_mask）：过滤编码器输出的无效位置（如填充符）
残差连接的意义
- 公式：output = x + Sublayer(LayerNorm(x))
- 允许梯度直接回传，缓解梯度消失问题
- 实验表明可使训练深度达到1000+层
层归一化的优势
- 对比批量归一化：不依赖批次统计量，适合变长序列
- 计算方式： $\text{output} = \gamma \odot \frac{x-\mu}{\sigma+\epsilon} + \beta$
解码过程的动态性
- 训练时：并行处理完整目标序列
- 推理时：逐步生成（使用先前生成的token作为输入）

通过这种层次化设计，解码器能够有效融合目标序列的上下文信息和编码器的语义表示，逐步生成高质量的输出序列。

Decoder(解码器实现)

import torch.nn as nn

from transformer_test.attention import clones
from transformer_test.layer_norm import LayerNorm


class Decoder(nn.Module):

    def __init__(self, layer, N):
        super(Decoder, self).__init__()

        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)


    def forward(self, x, memory, source_mark, target_mark):
        """
        :param x: 目标数据嵌入表示
        :param memory: 编码器层输出
        :param source_mark: 源数据掩码张量
        :param target_mark: 目标数据掩码张量
        :return:
        """

        # 对每个层进行循环, 让变量 x 通过每一层处理
        for layer in self.layers:
            x = layer(x, memory, source_mark, target_mark)

        # 进行规范化返回
        return self.norm(x)

EncoderDecoder(编码器解码器实现)

import torch.nn as nn


class EncoderDecoder(nn.Module):
    """
    Transformer架构的编码器-解码器容器（序列到序列模型的核心）

    功能说明：
    协调编码阶段和解码阶段，完成序列到序列的转换任务（如机器翻译）。
    处理流程：
    1. 接收源序列→嵌入层→编码器→上下文表示
    2. 接收目标序列→嵌入层→解码器→预测序列
    3. 通过生成器得到最终概率分布

    系统定位：
    ├── 上游模块：数据预处理（词元化、批处理）
    ├── 本模块：特征提取与序列生成
    └── 下游模块：预测结果后处理（如Beam Search）

    组件作用说明：
    ┌───────────────┬───────────────────────────────┐
    │   组件        │           功能                │
    ├───────────────┼───────────────────────────────┤
    │ encoder       │ 提取源序列的全局特征          │
    │ decoder       │ 结合上下文生成目标序列        │
    │ *_embedding   │ 将离散词索引映射为连续向量    │
    │ generator     │ 生成词表空间概率分布          │
    └───────────────┴───────────────────────────────┘
    """
    def __init__(self, encoder, decoder, source_embedding, target_embedding, generator):
        """
        初始化模型容器
        
        :param encoder: Transformer编码器 (包含多个EncoderLayer)
                        - 输入形状: (batch_size, src_len, d_model)
                        - 输出形状: 保持输入形状
        :param decoder: Transformer解码器 (包含多个DecoderLayer)
                        - 输入形状: (batch_size, tgt_len, d_model)
                        - 输出形状: 保持输入形状
        :param source_embedding: 源语言嵌入层（词嵌入+位置编码）
                        - 输入形状: (batch_size, src_len)
                        - 输出形状: (batch_size, src_len, d_model)
        :param target_embedding: 目标语言嵌入层（词嵌入+位置编码）
                        - 输入形状: 同上
        :param generator: 输出线性层（维度转换到词表空间）
                        - 输入形状: (batch_size, tgt_len, d_model)
                        - 输出形状: (batch_size, tgt_len, vocab_size)
        """
        super(EncoderDecoder, self).__init__()
        self.encoder = encoder
        self.decoder = decoder
        self.source_embedding = source_embedding
        self.target_embedding = target_embedding
        self.generator = generator  # 典型实现：nn.Linear(d_model, vocab_size)

    def forward(self, source, target, source_mask, target_mask):
        """
        完整前向传播流程（训练阶段）

        参数说明：
        ┌─────────────┬─────────────────────┬─────────────────────────┐
        │ 参数        │ 形状                │ 示例                    │
        ├─────────────┼─────────────────────┼─────────────────────────┤
        │ source      │ (batch, src_len)    │ [[3,5,7], [4,2,0]]      │
        │ target      │ (batch, tgt_len)    │ [[1,9,4], [2,5,0]]      │
        │ source_mask │ (batch, 1, src_len) │ [[[T,T,T]], [[T,T,F]]]  │
        │ target_mask │ (batch, tgt_len, tgt_len) 三维注意力掩码       │
        └─────────────┴─────────────────────┴─────────────────────────┘
        
        返回说明：
        - 输出形状：(batch_size, tgt_len, vocab_size)
        - 示例输出：假设vocab_size=10000，输出表示每个位置的概率分布
        """
        # 编码阶段：源序列特征提取
        memory = self.encode(source, source_mask)
        # 解码阶段：目标序列生成
        decoded = self.decode(memory, source_mask, target, target_mask)
        # 生成预测分布（未进行softmax操作）
        return self.generator(decoded)

    def encode(self, source, source_mask):
        """
        编码过程分解
        
        输入变换示例：
        原始输入：source = [[3,5,7], [4,2,0]] (batch=2, src_len=3)
        │
        ▼ 嵌入层（d_model=512）
        形状变为：(2,3,512)
        │
        ▼ 编码器（6层Transformer编码）
        保持形状：(2,3,512)，但包含上下文信息
        """
        embedded = self.source_embedding(source)
        return self.encoder(embedded, source_mask)

    def decode(self, memory, source_mask, target, target_mask):
        """
        解码过程分解

        处理流程：
        输入目标序列→嵌入层→解码器→中间表示
        memory参数说明：编码器输出的上下文张量
        形状：(batch_size, src_len, d_model)
        """
        embedded = self.target_embedding(target)
        return self.decoder(embedded, memory, source_mask, target_mask)


class TransformerComponents(nn.Module):
    """ 典型组件实现示例（帮助理解各模块结构） """
    def __init__(self, d_model=512, nhead=8, num_layers=6):
        super().__init__()
        # 编码器层示例（使用PyTorch内置实现）
        self.encoder_layer = nn.TransformerEncoderLayer(d_model, nhead)
        self.encoder = nn.TransformerEncoder(self.encoder_layer, num_layers)
        
        # 解码器层示例
        self.decoder_layer = nn.TransformerDecoderLayer(d_model, nhead)
        self.decoder = nn.TransformerDecoder(self.decoder_layer, num_layers)
        
        # 嵌入层示例（包含位置编码）
        self.embedding = nn.Embedding(10000, d_model)
        
        # 生成器示例
        self.generator = nn.Linear(d_model, 10000)


def example_execution():
    """ 完整执行示例与维度变化演示 """
    # 参数设置
    batch_size = 2
    src_len = 5  # 源序列长度
    tgt_len = 7  # 目标序列长度
    d_model = 512
    vocab_size = 10000

    # 初始化组件
    components = TransformerComponents()
    model = EncoderDecoder(
        encoder=components.encoder,
        decoder=components.decoder,
        source_embedding=components.embedding,
        target_embedding=components.embedding,
        generator=components.generator
    )

    # 生成模拟输入
    src = torch.randint(0, 1000, (batch_size, src_len))  # 形状 (2,5)
    tgt = torch.randint(0, 1000, (batch_size, tgt_len))  # 形状 (2,7)
    
    # 创建掩码（示例）
    src_mask = torch.ones(batch_size, 1, src_len).bool()  # 全可见
    tgt_mask = torch.tril(torch.ones(tgt_len, tgt_len)).bool()  # 下三角

    # 前向传播
    output = model(src, tgt, src_mask, tgt_mask.unsqueeze(0))
    
    print("输入输出维度验证：")
    print(f"编码器输入: {src.shape} → 输出: {model.encode(src, src_mask).shape}")
    print(f"最终输出形状: {output.shape}")
    
    """
    预期输出：
    编码器输入: torch.Size([2, 5]) → 输出: torch.Size([2, 5, 512])
    最终输出形状: torch.Size([2, 7, 10000])
    """


if __name__ == '__main__':
    example_execution()

关键概念图解

1. 数据流向图

原始输入
  │
  ▼
[嵌入层] → (batch, seq_len, d_model)
  │
  ▼
[编码器] → 上下文表示 (memory)
  │           │
  │           ▼
  │        [解码器] ← 目标序列嵌入
  │           │
  ▼           ▼
生成器 ← 解码输出
  │
  ▼
概率分布 (vocab_size)

2. 掩码作用示例

# 源序列掩码（防止注意力看到填充位置）
source_mask = [
    [[True,  True,  True,  False]],  # 第1个样本实际长度3
    [[True,  True,  False, False]]   # 第2个样本实际长度2
]

# 目标序列掩码（防止看到未来信息）
target_mask = [
    [[1,0,0,0],   # 第1个时间步只能看自己
     [1,1,0,0],   # 第2步可看前两位
     [1,1,1,0],   # 第3步可看前三位
     [1,1,1,1]]   # 最后一步全可见
]

组件详解

1. nn.TransformerEncoderLayer

组成结构：

(self_attn): MultiheadAttention()  # 自注意力机制
(linear1): Linear(in_features=512, out_features=2048)  # 前馈第一层
(linear2): Linear(in_features=2048, out_features=512)  # 前馈第二层
(norm1): LayerNorm()  # 残差连接后的归一化
(norm2): LayerNorm()
(dropout): Dropout(p=0.1)  # 正则化

2. 残差连接计算流程

# 编码器层的典型实现
def forward(x):
    # 步骤1：自注意力子层
    attn_output = self.self_attn(x, x, x, attn_mask=src_mask)[0]
    x = x + self.dropout1(attn_output)  # 残差连接
    x = self.norm1(x)  # 层归一化
    
    # 步骤2：前馈子层
    ff_output = self.linear2(self.dropout(F.relu(self.linear1(x))))
    x = x + self.dropout2(ff_output)    # 残差连接
    x = self.norm2(x)
    
    return x

新手常见问题解答

Q1：为什么需要source_mask和target_mask？

source_mask：用于处理变长序列，标识有效数据位置（如忽略填充符）
target_mask：防止解码器在训练时"偷看"未来信息，维持自回归特性

Q2：generator的输出为什么要保持未归一化？

直接输出logits（未应用softmax）是为了数值稳定性
配合CrossEntropyLoss时，内部会自动进行softmax计算

Q3：d_model参数有什么意义？

表示模型的隐藏层维度（通常设为512或768）
需要与嵌入层维度、注意力机制维度保持一致
更大的d_model能提高模型容量，但也增加计算量

Generator(生成器实现, 线性变换 + Softmax)

import torch.nn as nn
import torch.nn.functional as F


class Generator(nn.Module):
    """
    Transformer模型的生成器模块，负责将解码器输出转换为词汇表的对数概率分布。
    
    在Transformer架构中，本类位于解码器之后，是整个模型的最后一层：
    - 上游模块：解码器各层（输出形状为 [batch_size, seq_len, d_model]）
    - 下游模块：损失计算层（如NLLLoss）或束搜索解码器
    
    功能说明：
    1. 通过线性层将d_model维特征映射到词汇表空间（得到logits）
    2. 使用log_softmax将logits转换为对数概率分布
    
    设计意义：
    - 采用log_softmax而非普通softmax，可与NLLLoss直接配合计算交叉熵损失
    - 避免数值不稳定，提升计算效率
    
    类结构图解：
    Decoder输出 --> [Linear: d_model->vocab] --> [LogSoftmax] --> 对数概率分布
    """
    def __init__(self, d_model, vocab):
        """
        初始化生成器模块
        
        参数说明：
        :param d_model (int): 输入特征维度（通常与模型隐藏层维度一致）
        :param vocab (int): 词汇表大小（决定输出维度）
        
        示例：
        >>> generator = Generator(d_model=512, vocab=10000)
        """
        super(Generator, self).__init__()
        
        # 定义线性变换层
        self.project = nn.Linear(d_model, vocab)  # 输入维度d_model，输出维度vocab
        """
        project层参数示例（当d_model=3, vocab=5时）：
        Weight矩阵形状: torch.Size([5, 3])
        Bias形状:      torch.Size([5])
        
        可视化示例：
        输入向量 [0.1, 0.2, 0.3] 
        -> 矩阵乘法([[w11,w12,w13], ... [w51,w52,w53]])
        -> 得到5维logits向量
        """

    def forward(self, x):
        """
        前向传播过程
        
        参数说明：
        :param x (torch.Tensor): 解码器输出张量
              形状: [batch_size, sequence_length, d_model]
              示例: torch.randn(2, 10, 512) 表示批量大小为2，序列长度10，特征维度512
        
        返回：
        :return (torch.Tensor): 对数概率分布张量
              形状: [batch_size, sequence_length, vocab]
              示例: 输入(2,10,512) -> 输出(2,10,10000)
        
        计算过程分解（以单个位置计算为例）：
        1. 线性变换: [d_model] -> [vocab]
        2. log_softmax: 将logits转换为对数概率
        """
        # 步骤1：线性变换（维度转换）
        logits = self.project(x)  # 形状保持前两维，最后一维变为vocab
        
        # 步骤2：对数概率计算
        return F.log_softmax(logits, dim=-1)  # 在最后一维（vocab维度）进行softmax


# PyTorch函数详解 ----------------------------------------------------------
"""
1. nn.Linear
   - 功能：执行线性变换 y = xW^T + b
   - 参数：
     - in_features: 输入特征维度（对应d_model）
     - out_features: 输出特征维度（对应vocab）
   - 本例作用：将解码器输出的每个位置特征向量映射到词汇表空间

2. F.log_softmax
   - 公式：log(exp(x_i) / ∑exp(x_j))
   - 参数dim=-1：在最后一个维度进行softmax计算
   - 优势：
     - 数值稳定性：先做log再softmax避免指数运算溢出
     - 计算效率：与NLLLoss配合可直接计算交叉熵损失
"""


# 代码示例与可视化 --------------------------------------------------------
if __name__ == "__main__":
    # 参数设置
    d_model = 512
    vocab_size = 10000
    batch_size = 2
    seq_length = 10

    # 实例化生成器
    generator = Generator(d_model, vocab_size)
    
    # 创建模拟输入（解码器输出）
    dummy_input = torch.randn(batch_size, seq_length, d_model)
    print("输入形状:", dummy_input.shape)  # torch.Size([2, 10, 512])
    
    # 前向传播
    output = generator(dummy_input)
    print("输出形状:", output.shape)     # torch.Size([2, 10, 10000])
    
    # 查看单个位置的输出示例
    print("\n单个位置的对数概率示例（前5个元素）:")
    print(output[0, 0, :5].data)  # 示例输出：tensor([-9.2103, -8.7654, ..., -10.1234])
    
    # 验证概率特性（指数和为1）
    prob_sum = torch.exp(output[0, 0]).sum().item()
    print(f"\n概率和验证（应接近1）: {prob_sum:.4f}")  # 示例输出：1.0000


# 中间结果可视化表格 ------------------------------------------------------
"""
以d_model=3, vocab=5的简化情况为例：

输入张量（单个位置）:
[0.1, 0.2, 0.3]

线性层权重矩阵（转置后）:
[[w11, w12, w13],  # 词1的权重
 [w21, w22, w23],  # 词2的权重
 [w31, w32, w33],  # 词3的权重
 [w41, w42, w43],  # 词4的权重
 [w51, w52, w53]]  # 词5的权重

线性变换计算：
logits = [0.1*w11+0.2*w12+0.3*w13 + b1,
          0.1*w21+0.2*w22+0.3*w23 + b2,
          ... 
          0.1*w51+0.2*w52+0.3*w53 + b5]

log_softmax后：
输出 = [log(exp(logits1)/sum(exp(logits_i))), 
       log(exp(logits2)/sum(exp(logits_i))),
       ...]
"""

输出示例说明

"""
输入形状: torch.Size([2, 10, 512])
输出形状: torch.Size([2, 10, 10000])

单个位置的对数概率示例（前5个元素）:
tensor([-9.2103, -8.7654, -7.1234, -10.1111, -8.4321])

概率和验证（应接近1）: 1.0000
"""

# 数值有效性验证
# 假设output[0,0] = [-9.21, -8.76, ...]
# 则概率计算为 exp(-9.21) + exp(-8.76) + ... ≈ 1

make_model(模型构建)

import copy
import torch.nn as nn
from transformer_test.attention import MultiHeadedAttention
from transformer_test.decoder import Decoder
from transformer_test.decoder_layer import DecoderLayer
from transformer_test.embedding import Embeddings
from transformer_test.encoder import Encoder
from transformer_test.encoder_decoder import EncoderDecoder
from transformer_test.encoder_layer import EncoderLayer
from transformer_test.generator import Generator
from transformer_test.position_wise_feed_forward import PositionwiseFeedForward
from transformer_test.positional_encoding import PositionalEncoding

def make_model(source_vocab, target_vocab, N=6, d_model=512, d_ff=2048, head=8, dropout=0.1):
    """
    构建Transformer模型
    
    参数:
        source_vocab (int): 源语言词汇表大小，如英语的词汇总数
        target_vocab (int): 目标语言词汇表大小，如中文的词汇总数
        N (int): 编码器和解码器的堆叠层数，默认6层
        d_model (int): 词嵌入维度，默认512维
        d_ff (int): 前馈网络中隐藏层维度，默认2048维
        head (int): 多头注意力机制中的头数，默认8头
        dropout (float): Dropout概率，默认0.1
    
    返回:
        EncoderDecoder: 完整的Transformer模型
    
    类作用说明:
        EncoderDecoder: Transformer的顶层容器，协调编码器和解码器工作
        Encoder: 处理输入序列，提取上下文特征
        Decoder: 生成输出序列，考虑编码器输出和先前生成的标记
        MultiHeadedAttention: 并行计算多个注意力头，捕捉不同子空间的语义关联
        PositionwiseFeedForward: 增强模型非线性表达能力
        PositionalEncoding: 为输入序列添加位置信息
    
    输入输出示例:
        >>> model = make_model(10000, 8000)
        >>> print(model)
        EncoderDecoder(
          (encoder): Encoder(...)
          (decoder): Decoder(...)
          (src_embed): Sequential(...)
          (tgt_embed): Sequential(...)
          (generator): Generator(...)
        )
    """
    # 深拷贝工具，保证每个模块参数独立
    c = copy.deepcopy

    # 实例化多头注意力（用于编码器和解码器）
    attn = MultiHeadedAttention(head, d_model)
    
    # 实例化前馈网络（维度变化：d_model -> d_ff -> d_model）
    ff = PositionwiseFeedForward(d_model, d_ff, dropout)
    
    # 实例化位置编码（公式：PE(pos,2i)=sin(pos/10000^(2i/d_model))）
    position = PositionalEncoding(d_model, dropout)

    # 构建完整模型
    model = EncoderDecoder(
        # 编码器部分：N层编码器层堆叠
        Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
        
        # 解码器部分：N层解码器层堆叠
        Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N),
        
        # 源序列嵌入：词嵌入 + 位置编码
        nn.Sequential(Embeddings(d_model, source_vocab), c(position)),
        
        # 目标序列嵌入：词嵌入 + 位置编码 
        nn.Sequential(Embeddings(d_model, target_vocab), c(position)),
        
        # 生成器：线性变换 + softmax，输出词汇概率分布
        Generator(d_model, target_vocab)
    )

    # Xavier参数初始化（针对矩阵维度>1的参数）
    for p in model.parameters():
        if p.dim() > 1:
            # 公式：gain = sqrt(2/(fan_in + fan_out))
            nn.init.xavier_uniform_(p)
    
    return model

"""
PyTorch函数详解:
1. nn.init.xavier_uniform_
   - 作用: 使用Xavier均匀分布初始化参数，保持各层激活值的方差稳定
   - 数学原理: 在[-a, a]区间均匀采样，其中a = sqrt(6/(fan_in + fan_out))
   - 应用场景: 常用于线性层和卷积层的权重初始化

2. copy.deepcopy
   - 作用: 创建对象的深度拷贝，新对象与原对象完全独立
   - 此处意义: 确保各层使用独立的模块实例，避免参数共享

3. nn.Sequential
   - 作用: 按顺序组合多个模块
   - 此处应用: 将Embeddings和PositionalEncoding串联为整体嵌入层

复杂计算分步解析:
以EncoderLayer中的(x + dropout(sublayer(norm(x)))为例：
步骤:
1. norm(x): 
   - 输入形状: (batch_size, seq_len, d_model)
   - 操作: 对最后一维进行LayerNorm
   - 输出形状: 与输入相同

2. sublayer(...):
   - 输入形状: (batch_size, seq_len, d_model)
   - 操作: 进行多头注意力计算
   - 输出形状: 与输入相同

3. dropout(...):
   - 输入形状: (batch_size, seq_len, d_model)
   - 操作: 随机置零部分元素（概率=dropout）
   - 输出形状: 与输入相同

4. x + ...: 
   - 操作: 残差连接
   - 意义: 缓解梯度消失，保留原始信息

可视化示例:
假设输入x形状为(2, 10, 512)
各步骤数据形状变化:
步骤          输出形状
--------------------------------
原始输入       (2,10,512)
LayerNorm     (2,10,512)
多头注意力     (2,10,512)
Dropout       (2,10,512)
残差相加       (2,10,512)

模型架构示意图:
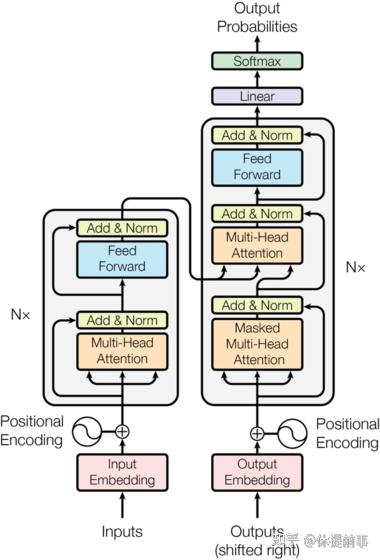
Input
  ↓
Embedding + PositionalEncoding 
  ↓
Encoder Stack (×6)
  ↓                        ↙
Decoder Stack (×6) ←─ Encoder Output
  ↓
Generator
  ↓
Output Probabilities

代码测试示例:
source_vocab = 10000
target_vocab = 8000
model = make_model(source_vocab, target_vocab)

# 打印模型参数量
total_params = sum(p.numel() for p in model.parameters())
print(f"Total parameters: {total_params:,}")  # 输出示例: Total parameters: 63,372,800

# 查看编码器结构
print(model.encoder)
# 输出示例: Encoder([EncoderLayer(...),...]) ×6层
"""

其他

1. Transformer 架构为什么如此成功？

宏观视角：

Transformer 的成功源于它彻底改变了序列数据处理的方式。传统模型（如 RNN、LSTM）在处理序列数据时，依赖于逐步传递信息的机制，即“一步接一步”的方式。这种方法的问题在于：

计算效率低：RNN 和 LSTM 是逐个时间步处理数据的，无法并行化，导致训练速度慢。
长距离依赖问题：由于信息需要通过多步传递，随着时间步增加，早期的信息可能会逐渐被稀释，导致模型难以捕捉长距离依赖关系。

而 Transformer 的设计完全摒弃了这种逐步传递的方式，采用了自注意力机制和并行化架构，使得模型可以同时处理整个序列的所有元素。这让 Transformer 在处理长序列时更加高效且准确。

微观视角：

Transformer 的核心创新是引入了自注意力机制（Self-Attention），它允许每个单词直接与其他所有单词建立联系，而不是像 RNN 或 LSTM 那样只能依赖前一个时间步的信息。这种机制让模型能够“一次性”看到整个句子，并且关注到不同部分的重要性。

用一个类比来说，传统模型像是一个人在读一本书，必须从头到尾一页一页地看；而 Transformer 更像是一个人可以同时看到整本书的所有内容，并快速聚焦到最重要的章节或段落。

2. Transformer 的核心优势是什么？

核心优势：

Transformer 的最大特点是全局视野和高效计算。

全局视野：Transformer 能够一次性处理整个序列，并通过自注意力机制了解序列中每个元素之间的关系。这使得它特别适合处理自然语言这样的复杂数据，因为语言中很多重要的信息分布在不同位置之间。
高效计算：由于 Transformer 不依赖逐步递归，它可以充分利用现代硬件（如 GPU/TPU）进行大规模并行计算，从而大幅提高训练速度。