~《概率论》~概率的性质条件概率与事件的独立性

本文链接：https://blog.csdn.net/weixin_44715384/article/details/105064108

本文深入探讨了概率论中的关键概念，包括条件概率的定义及其与并事件的区别，概率的乘法公式，事件独立性的性质和证明，以及全概率公式的应用。通过实例解析，帮助读者更好地掌握这些概率论基础。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

_{《概率论》}概率的性质条件概率与事件的独立性

文章目录

一、条件概率

定义：设A,B为任意两个事件，且P(B)>0，则称

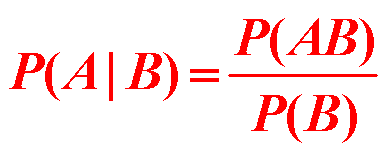
为事件B发生条件下，事件A发生的条件概率。
条件概率满足概率的所有性质，如：

p(φ|B)=0, p(Ω|B)=1
P(AB)与P(A|B)的区别与联系：
联系：
两个都是在A,B发生情况下计算概率。
区别：
(1) P(AB) 表示A,B同时发生的概率；P(A|B) 表示在B发生条件下A发生的概率，事件A,B的发生有先后次序。
(2) P(AB) 的样本空间是，P(A|B)的样本空间是B。

二、概率的乘法公式

定义：设A,B为任意两个事件，若P(A)>0, P(B)>0，则有称该式为概率的乘法公式。
推广：设A1,A2,…，An为任意n个事件，且 $p(A_1A_2\cdot\cdot\cdot A_{n-1})>0$ ,则有 $P(A_1A_2\cdot\cdot\cdot A_n) = P(A_1)P(A_2|A_1)P(A_3|A_1A_2)\cdot\cdot\cdot P(A_n|A_1A_2\cdot\cdot\cdot A_{n-1})$

在这里插入图片描述

三、事件的独立性

定义：设A,B为随机试验E的任意两个事件,若满足：则称事件A,B相互独立，简称独立。
必然事件及不可能事件与任意事件A相互独立。
前提：A和B独立。若P(B)>0，则P(A|B)=P(A).
证明：如果P(A)=0或者P(A)=1，则A与任何事件独立
A,B独立不同于A,B互斥、对立的概念。
A,B独立与A,B互不影响之间的关系。
性质：定理:设A,B为任意两个事件,则 $A,B;A,\bar{B};\bar{A},B;\bar{A},\bar{B}$ 四组事件的独立性等价。
事件A，B独立等价于：
推广：
另外：
n个事件A1,A2,…,An独立，则部分用其对立事件替换，所得新的n个事件仍然相互独立。
独立事件概率的计算：
$P(A_1A_2\dots A_n) =\displaystyle\prod_1^nP(A_i)$
$P(A_1+A_2+\dots+A_n) = 1-\displaystyle\prod_1^nP(\bar{A_i})$

四、全概率公式

在这里插入图片描述

置项：写好博客，参照here 或者复制打开下面链接

https://blog.csdn.net/cungudafa/article/details/84658703?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task

置项：使用LaTeX数学公式，参照here或者复制打开下面链接