通过K-mean方法实现wine数据集聚类

一、题目

利用K-mean聚类方法，完成wine数据集聚类

二、实现思路

读取数据集——标准化数据集——定义分类数量——执行K-mean分类——分类可视化

三、代码实现

%读取数据集
date=readtable('winequality-red.csv');

%将数据转换为double型
date_part1=table2array(date(:,1:end));

%标准化数据
[date_part, mu, sigma] = zscore(date_part1);

%定义类别数量
numclusters=3;
%执行聚类
[idx,C]=kmeans(date_part,numclusters);

%可视化
figure;
gscatter(date_part(:,1),date_part(:,2), idx);
hold on;
plot(C(:,1), C(:,2), 'ko', 'MarkerSize', 10);
legend('Cluster 1', 'Cluster 2', 'Cluster 3', 'Centroids');
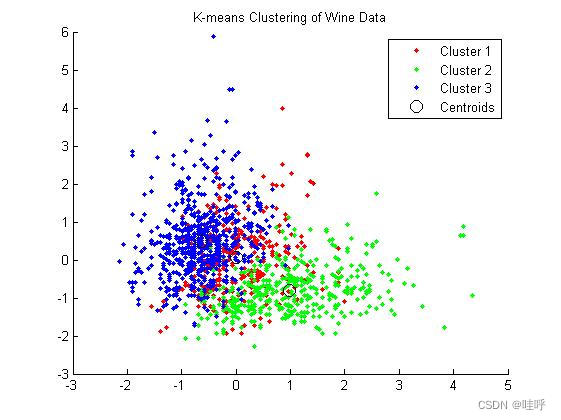
title('K-means Clustering of Wine Data');

四、运行结果