主成分分析

1.引言

       本节在清风数学建模学习的同时结合《应用多元统计分析》（王学民）内容，为大家介绍主成分分析（Principal Component Analysis ,PAC)，侧重讲基本思想、具体应用及代码，但主成分分析深入学习需要有较强的线性代数和多元统计基础。

2.主成分分析概念及基本思想

2.1概念

       在对数据进行分析时，涉及的样品往往是有多个指标，较多的指标会给分析带来复杂，而且指标之间常常存在一定程度的相关性，有时甚至存在相当高的相关性。这就使含在观测数据中的信息在一定程度上有所重迭，势必会增加分析问题的难度，这时我们有必要对变量进行降维，从而使问题的分析得以简化。

       主成分分析就是设法将原来指标重新组合成一组新的互相无关的几个综合指标来代替原来指标。根据实际需要从中可取几个较少的综合指标尽可能多地反映原来的指标的信息。这种将多个指标化为少数相互无关的综合指标的统计方法叫做主成分分析。在数学上也是处理降维的一种方法。

       这些综合指标是原来多个指标的线性组合，虽然这些综合指标是不能直接观测到，但这些综合指标之间互不相关，且能反映原来那些指标的大部分信息。（变量的变异性越大，说明它对各种场景的“遍历性”越强，提供的信息就更加充分，反映的信息量就越大。主成分分析中的信息，就是指标的变异性，用标准差或方差表示它。）

2.2基本思想

       主成分分析就是将原来众多具有一定相关性的指标重新组合成一组新的相互无关的综合指标来代替原来指标。通常数学上的处理是将原来p个指标作线性组合，作为新的综合指标，如果将选取的第一个线性组合即第一个综合指标记为，自然希望尽可能多的反映原来指标的信息，“信息”用的方差来表示， 的方差越大，表示所包含的信息越多。因此在所有的线性组合中应使的方差最大的线性组合，称为第一主成分。

       如第一主成分不足以代表原来p个指标的信息，再考虑选取即第二个线性组合，为了有效反映原来的信息，已有的信息就不需要再出现在中，用数学语言表达就是要求Cov(, )=0，称为第二主成分，依此类推，可以构造出第三、第四，…，第p个主成分。

       不难想象这些主成分之间不仅不相关，而且方差依此递减。因此在实际工作中，就挑选前几个最大主成分，虽然这样做会损失一部分信息，但是由于它使我们抓住了主要矛盾，并从原来数据中提取出大部分信息，这种既减少了变量的数目又抓住了主要矛盾的做法有利于问题的分析和处理。因此主成分分析就是通过适当的变量替换，使新变量成为原变量的线性组合，并寻求主成分来分析事物的一种方法。

3.总体主成分分析的几何解释

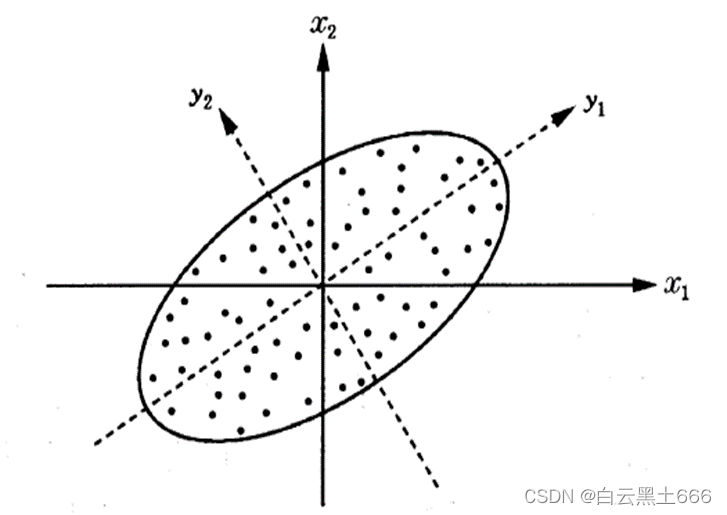
       假设只有两个变量x1，x2，有n个样品点，每个样品都测量了两个指标（X1,X2）,它们大致分布在一个矩形内。事实上，散点的分布总有可能沿着某一个方向略显扩张，这个方向我们就把它看作矩形的长边方向。显然在坐标系X1OX2里，单独看这n个点沿X1与X2都有较大的离散性，其离散程度可以用方差测定。如果将坐标旋转某个角度变成新坐标系y1Oy2，矩形的长边就是y1方向。

       从图可以看出，坐标旋转变换的目的是为了使得n个样本点在z1轴方向上的离散程度最大，即y1的方差最大，变量y1代表了原始数据的绝大部分信息，而在y2轴方向上n个样本点的波动很小，可以忽略不计，这样一来，二维问题就可以转化为一维问题来解决。 

4.样本主成分分析及步骤

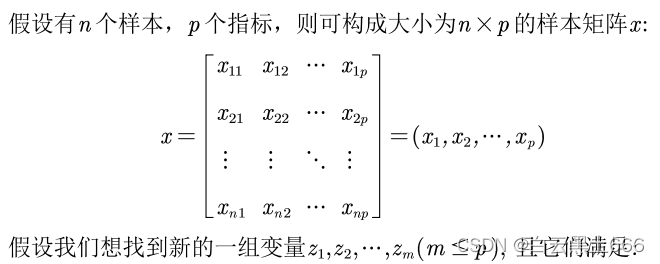
4.1 样本主成分分析

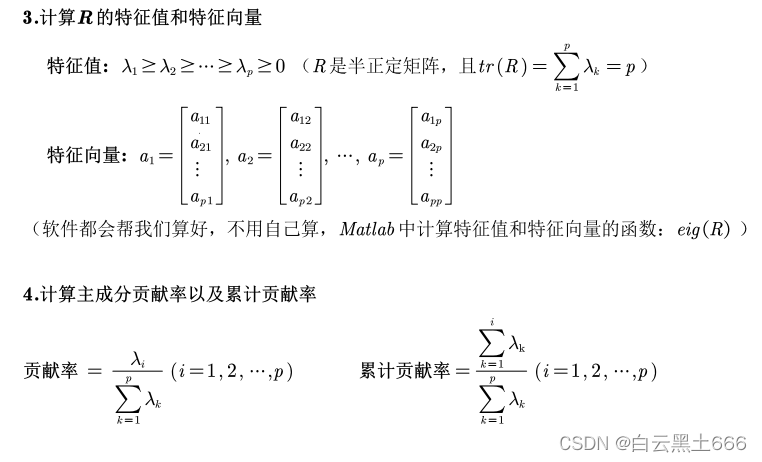
4.2主成分分析步骤

 注意：在对样本主成分分析进行实际意义解释时，

1）从系数的大小、系数的符号上进行分析；

2）系数绝对值较大，则表明该主成分主要综合了绝对值大的变量；

3）正号表示变量与主成分作用同方向，负号表示原变量与主成分作用反方向；

4）如果变量分组较有规则，则从特征向量各分量数值作出组内组间对比分析。

 4.3 例题

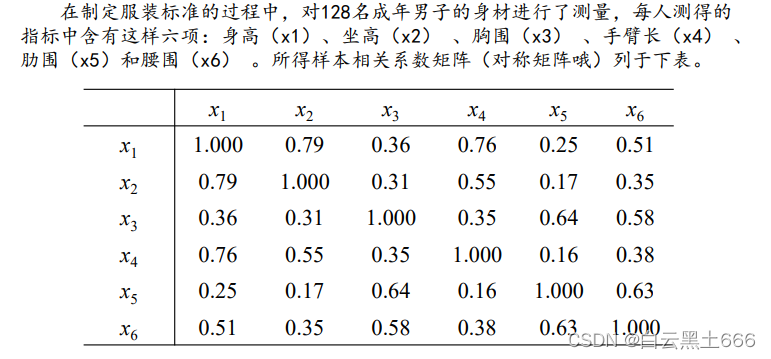
         第一步，直接计算变量之间的相关系数矩阵，

          第二步，计算相关系数矩阵的特征值、相应的特征向量以及贡献率 

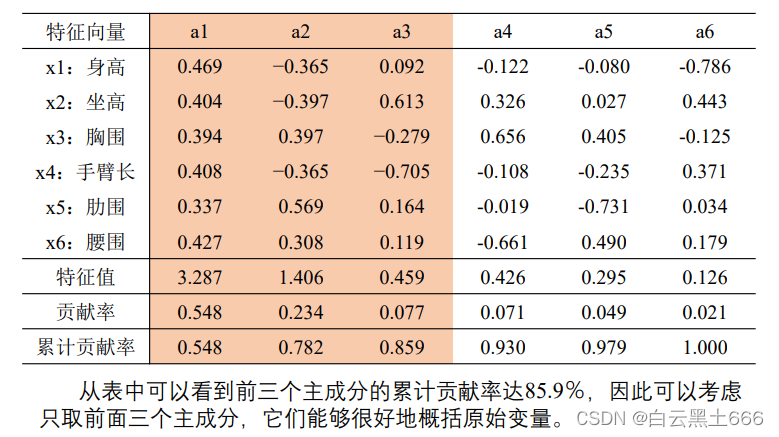
5.例题及代码

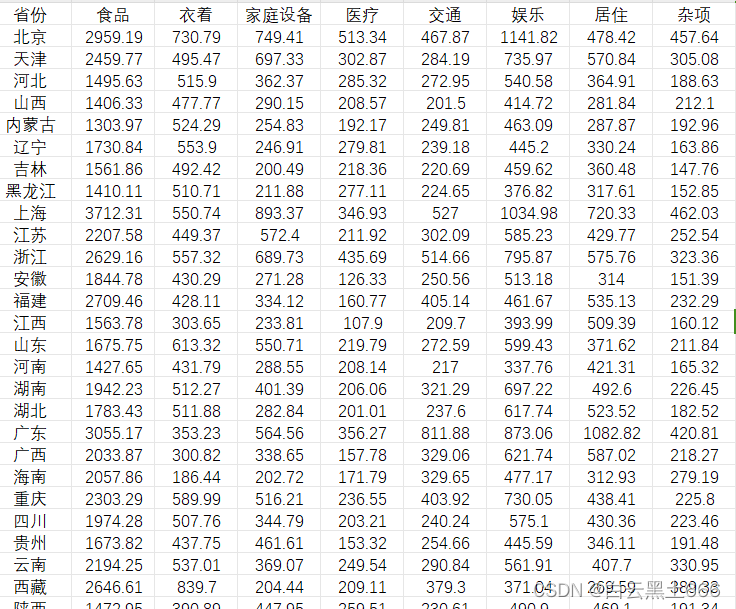
1999年全国31个省份城镇居民家庭平均每人全年消费性支出数据 .xlsx

[n,p] = size(x);  % n是样本个数，p是指标个数
%% 第一步：对数据x标准化为X
X=zscore(x);   % matlab内置的标准化函数（x-mean(x)）/std(x)
%% 第二步：计算样本协方差矩阵
R = cov(X);
%% 注意：以上两步可合并为下面一步：直接计算样本相关系数矩阵
R = corrcoef(x);
disp('样本相关系数矩阵为：')
disp(R)

%% 第三步：计算R的特征值和特征向量
% 注意：R是半正定矩阵，所以其特征值不为负数
% R同时是对称矩阵，Matlab计算对称矩阵时，会将特征值按照从小到大排列
[V,D] = eig(R);  % V 特征向量矩阵  D 特征值构成的对角矩阵

%% 第四步：计算主成分贡献率和累计贡献率
lambda = diag(D);  % diag函数用于得到一个矩阵的主对角线元素值(返回的是列向量)
lambda = lambda(end:-1:1);  % 因为lambda向量是从小大到排序的，我们将其调个头
contribution_rate = lambda / sum(lambda);  % 计算贡献率
cum_contribution_rate = cumsum(lambda)/ sum(lambda);   % 计算累计贡献率  cumsum是求累加值的函数
disp('特征值为：')
disp(lambda')  % 转置为行向量，方便展示
disp('贡献率为：')
disp(contribution_rate')
disp('累计贡献率为：')
disp(cum_contribution_rate')
disp('与特征值对应的特征向量矩阵为：')
% 注意：这里的特征向量要和特征值一一对应，之前特征值相当于颠倒过来了，因此特征向量的各列需要颠倒过来
%  rot90函数可以使一个矩阵逆时针旋转90度，然后再转置，就可以实现将矩阵的列颠倒的效果
V=rot90(V)';
disp(V)

6.主成分分析应用

       首先，最主要用于系统评估。其次，作为一种数据处理手段，与其它多元统计方法如回归分析、聚类分析结合使用。最后，主成分分析还可用于回归分析的自变量筛选。（聚类和回归会在后面给大家分享）

6.1聚类分析

       只有在指标个数特别多，且指标 之间存在很强的相关性时才用主成分聚类。接第5部分的例题，取第一主成分和第二主成分的值，将它们视为新的指标。导入SPSS中，进行聚类分析。

%% 计算我们所需要的主成分的值
m =input('请输入需要保存的主成分的个数:  ');
F = zeros(n,m);  %初始化保存主成分的矩阵（每一列是一个主成分）
for i = 1:m
ai = V(:,i)';   % 将第i个特征向量取出，并转置为行向量
Ai = repmat(ai,n,1);   % 将这个行向量重复n次，构成一个n*p的矩阵
F(:, i) = sum(Ai .* X, 2);  % 注意，对标准化的数据求了权重后要计算每一行的和
end
%%主成分聚类 ： 将主成分指标所在的F矩阵复制到Excel表格，然后再用Spss聚类
% 在Excel第一行输入指标名称（F1,F2, ..., Fm）
% 双击Matlab工作区的F,进入变量编辑中，然后复制里面的数据到Excel表格
% 导出数据之后，我们后续的分析就可以在Spss中进行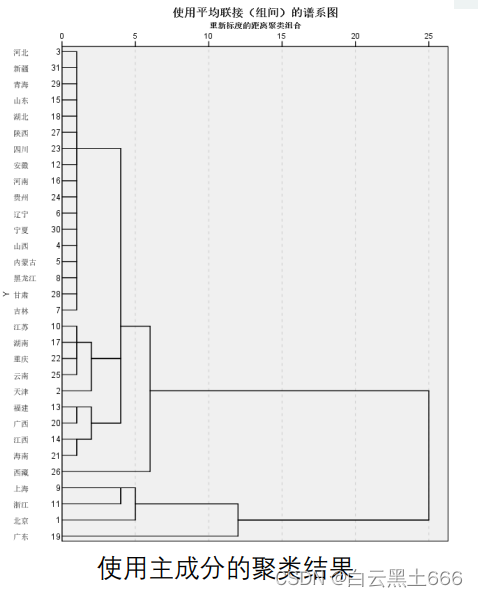

6.2回归分析-解决多重共线问题

      接第5部分的例题， 取第一主成分和第二主成分的值，将它们视为新的指标。导入stata中，Y是标准化后的

      reg  Y  F1  F2  %%Stata回归代码：

      estat imtest,white  %% Stata异方差检验代码

       主成分分析需要线性代数基础知识，我会专门写一篇线性代数的基础知识，方便大家继续学习因子分析、典型相关分析等。