CMOS模拟集成电路笔记 | 第六部分 | Chapter 9-10
如想获得更好的阅读体验,可以点击以下链接:CMOS模拟集成电路笔记-06
此为本系列笔记最后一部分,因为课本中的细节过多,作者能⼒有限,只能简要得写出⼀部分较为重要的内容供读者参考
第九章 运算放大器
9.1 概述
-
三要素法(对应例题9.2)
如下图:已知 V i n = a ⋅ u ( t ) V_{in}= a\cdot u(t) Vin=a⋅u(t),求输出阶跃响应:

三要素法公式:$f\left( t \right) =f\left( \infty \right) +\left( f\left( 0^+ \right) -f\left( \infty \right) e^{-\frac{t}{\tau}} \right) $.
-
当 V i n V_{in} Vin 刚开始变化时, V o u t ( 0 + ) = V o u t ( 0 − ) = 0 V_{out} (0^+)= V_{out} (0^-)= 0 Vout(0+)=Vout(0−)=0.
-
当 t ⟶ ∞ t \longrightarrow \infty t⟶∞, V i n ( ∞ ) = a u ( t ) V_{in}(\infty) = au(t) Vin(∞)=au(t), V o u t ( ∞ ) ⋅ R 1 ( R 1 + R 2 ) = V i n ( ∞ ) (由电路图分压公式得到) V_{out}(\infty)\cdot \frac{R_1}{(R_1+R_2)}=V_{in}(\infty) \text{(由电路图分压公式得到)} Vout(∞)⋅(R1+R2)R1=Vin(∞)(由电路图分压公式得到).
因此有:
V o u t ( ∞ ) = ( 1 + R 1 R 2 ) V i n ( ∞ ) = ( 1 + R 1 R 2 ) a u ( t ) V_{out}\left( \infty \right) =\left( 1+\frac{R_1}{R_2} \right) V_{in}\left( \infty \right) =\left( 1+\frac{R_1}{R_2} \right) au\left( t \right) Vout(∞)=(1+R2R1)Vin(∞)=(1+R2R1)au(t)
如此可求得 $V_{out}(\infty ),V_{out}(0^+)\text{和}\tau \text{(由电路图得到),并得到}f\left( t \right) \text{即}V\left( t \right) $ -
9.2 ⼀级运放
9.2.1 基本结构
-
简单的 单端输出 和 双端输出 结构的运放
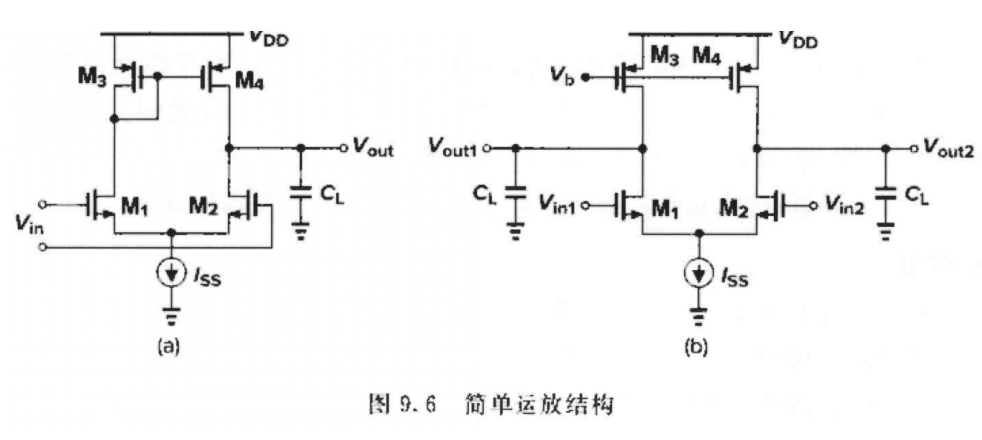
-
套筒式共源共栅运放
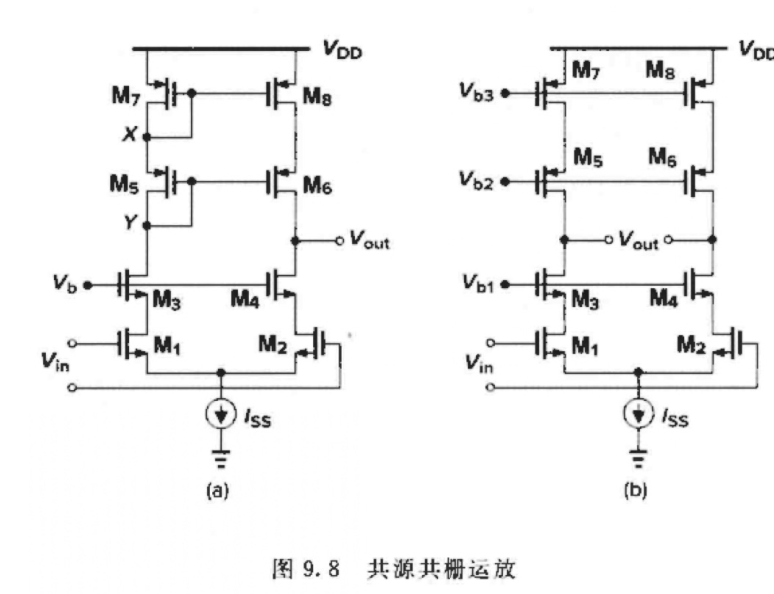
特点:采⽤⾼输出阻抗的⽅法实现⾼增益,采⽤Cascade结构减⼩输⼊管密勒效应(未理解)
9.2.4 折叠式共源共栅运放
套筒式共源共栅的缺点是:较⼩的输出摆幅和输⼊输出共模电平很难相同。
采⽤折叠式共源共栅:输⼊共模范围变⼤,同时带宽变⼩,增益降低,功耗和噪声较⼤.
9.3 两级运放
⼀般采⽤第⼀级提供⾼增益,第⼆级提供⼤的摆幅
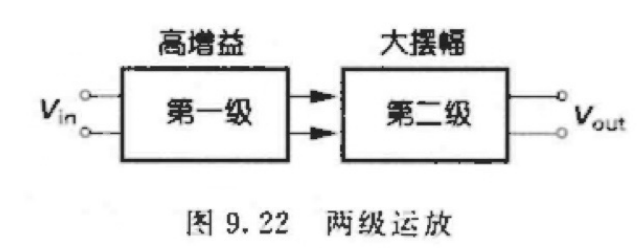
得到的总增益为各级增益之积,总带宽⽐每级带宽更⼩。
9.4 增益提高
9.4.1 基本思想
-
第⼀种观点:C-V负反馈提⾼输出阻抗

对于上⾯的负反馈结构,图(a)算得跨导:
G m = A 1 g m 1 + ( A 1 + 1 ) g m R s (如果没有 A 1 ) G m = g m 1 + ( A 1 + 1 ) g m R s \begin{array}{r} G_m=\frac{A_1 g _m}{1+\left( A_1+1 \right) g _mR_s}\\ \,\,\text{(如果没有}A_1\text{)}G_m=\frac{g _m}{1+\left( A_1+1 \right) g _mR_s}\\ \end{array} Gm=1+(A1+1)gmRsA1gm(如果没有A1)Gm=1+(A1+1)gmRsgm
图(b) 算得输出阻抗:
R o u t = r o + ( A 1 + 1 ) g m r o R s + R s (如果没有 A 1 )R o u t = r o + g m r o R s + R s \,\,\mathrm{R}_{\mathrm{out}}\,\,=r_o+\left( A_1+1 \right) g_mr_oR_s+R_s \\ \text{(如果没有}A_1\text{)R}_{\mathrm{out}}=r_o+g_mr_oR_s+R_s Rout=ro+(A1+1)gmroRs+Rs(如果没有A1)Rout=ro+gmroRs+Rs
表明该负反馈级将输出电阻提⾼的 A1倍,且仍可以保持其电压余度。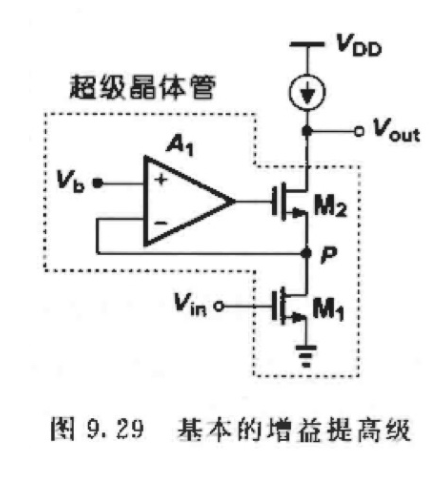
"超级晶体管"的实现:
- 输出阻抗为: r O 2 + ( A 1 + 1 ) g m 2 r O 2 r O 1 + r O 1 r_{O 2}+\left(A_{1}+1\right) g_{m 2} r_{O 2} r_{O 1}+r_{O 1} rO2+(A1+1)gm2rO2rO1+rO1.
- 等效跨导几乎等于 g m 1 g_{m1} gm1.
-
第⼆种观点:调节型共源共栅
放⼤器通过监控和箝位源电压来调节输出电流,即稳定输出电流= 增⼤输出电阻

计算得到 I o I_o Io和 I r o I_{ro} Iro⼏乎是⼤⼩相等,⽅向相反。也就是放⼤器调节栅电压使输出电流⼏乎不变化,表明增⼤的输出电阻。
9.7 共模反馈 CMFB
9.7.1 基本概念
CMFB的作⽤是针对电流源负载的全差动电路,确定输出直流CM电平。
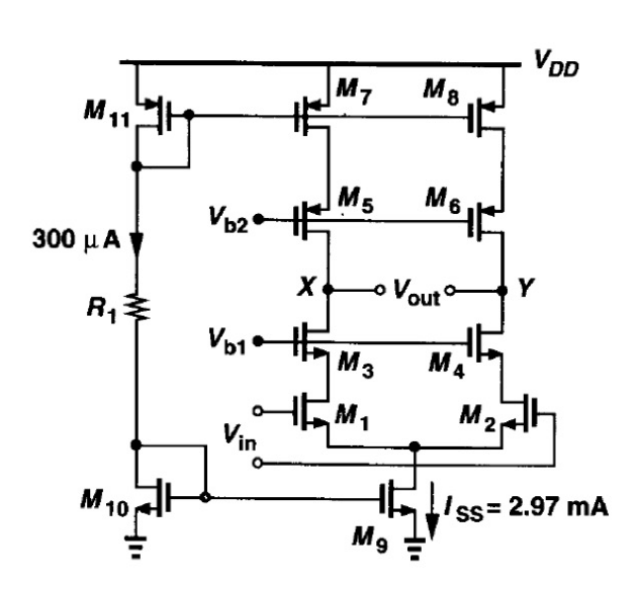
上图电路没有CMFB,上下电流源总电流不⼀致。将强制减少较⼤电流MOS管的电流,使上下电流⼀致,导致较⼤电流 MOS 管 VDS 减少,管⼦很可能进⼊线性区。
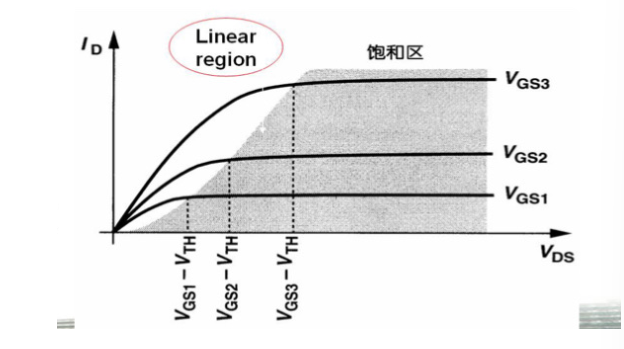
解释:
I
D
=
1
2
μ
n
C
O
X
W
L
(
V
G
S
−
V
T
n
)
2
(
1
+
λ
V
D
S
)
\mathrm{I}_{\mathrm{D}}=\frac{1}{2} \mu_{n} C_{O X} \frac{W}{L}\left(V_{G S}-V_{T_{n}}\right)^{2}\left(1+\lambda V_{D S}\right)
ID=21μnCOXLW(VGS−VTn)2(1+λVDS)
I
D
\mathrm{I}_{\mathrm{D}}
ID 稍有改变时, 因
λ
\lambda
λ 很小故
V
D
S
\mathrm{V}_{D S}
VDS 有较大改变
9.7.2 共模检测技术
⽬的是读取共模电平 Vout,CM
-
电阻检测的共模反馈
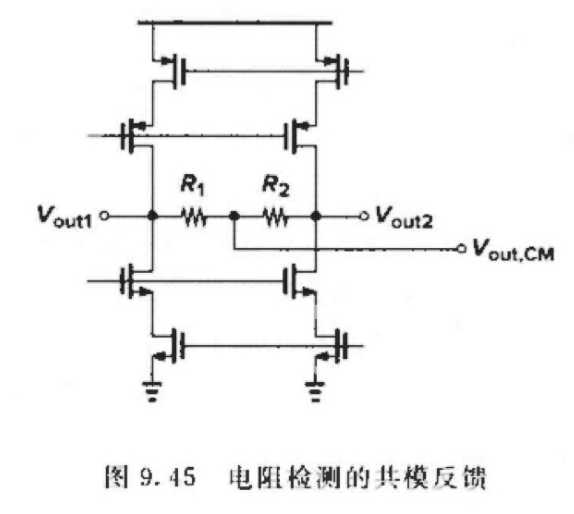
得到 V o u t , C M = ( V o u t 1 + V o u t 2 ) / 2 V_{out,CM} = (V_{out1}+ V_{out2})/ 2 Vout,CM=(Vout1+Vout2)/2
缺点:R1 和R2 必须⽐运放的输出阻抗⼤得多,避免开环增益降低。
-
采用源跟随器的共模反馈
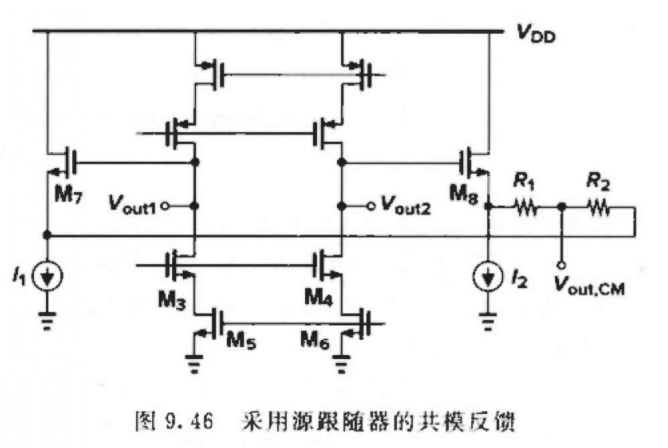
采⽤ SF 的共模反馈可以不需要⼤的电阻,但是要满⾜:
I 1 ≈ V out 2 − V out 1 R 1 + R 2 + I D 7 I_{1} \approx \frac{\mathrm{V}_{\text {out } 2}-\mathrm{V}_{\text {out } 1}}{R_{1}+R_{2}}+I_{\mathrm{D} 7} I1≈R1+R2Vout 2−Vout 1+ID7 -
另外⼀种CM检测⽅法:深线性区测量CM
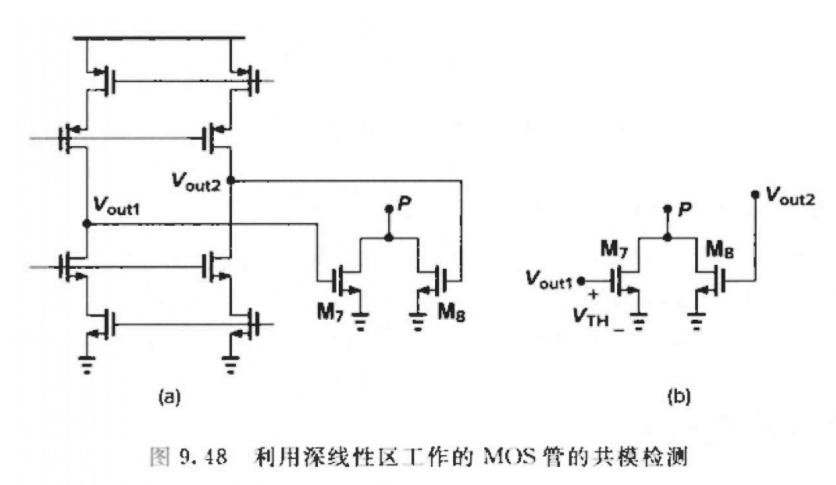
R t o t = 1 μ 0 C o x W L ( V o u t 1 + V o u t 2 − 2 V T H ) ( V o u t 1 + V o u t 2 = 2 V o u t , C M 与 R t o t 成反比) R_{\mathrm{tot}}=\frac{1}{\mu _0C_{\mathrm{ox}}\frac{W}{L}\left( V_{out1}+V_{\mathrm{out}2}-2V_{\mathrm{TH}} \right)} \\ \text{(}V_{out1}+V_{out2}=2V_{out,CM}\text{与}R_{tot}\text{成反比)} Rtot=μ0CoxLW(Vout1+Vout2−2VTH)1(Vout1+Vout2=2Vout,CM与Rtot成反比)
9.7.3 共模反馈技术
-
测量和控制输出CM电平
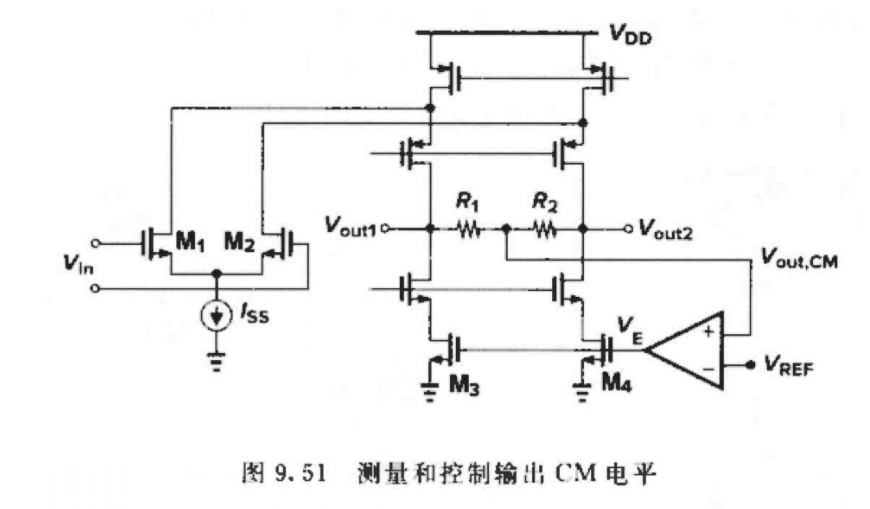
控制输出⽀路:使输出CM电平调整到设置的 VREF
-
另一种方法
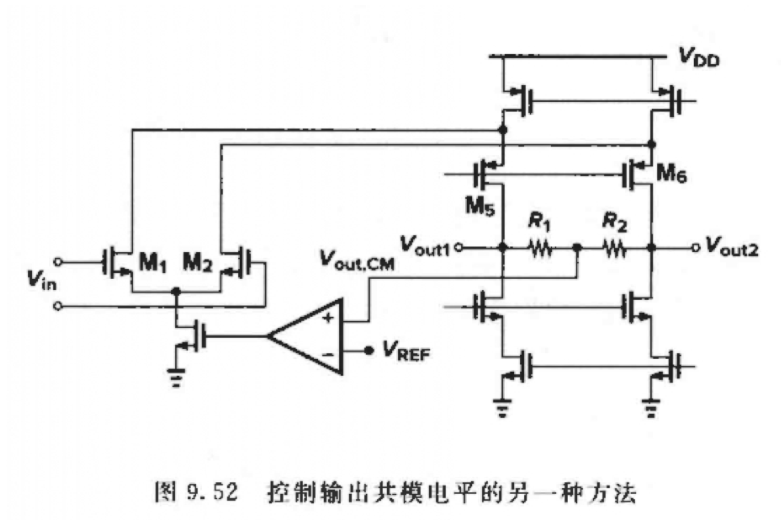
控制输⼊⽀路
-
采用线性器件的CMFB
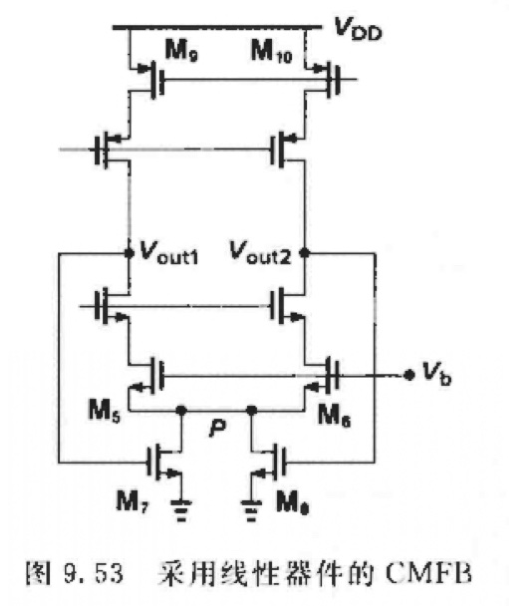
深线性区电阻CMFB技术调节输出:
V o u t 1 + V o u t 2 = 2 I D μ n C o x ( W L ) 7 , 8 1 V b − V G S 5 + 2 V T H V_{\mathrm{out} 1}+V_{\mathrm{out} 2}=\frac{2I_D}{\mu _nC_{ox}\left( \frac{W}{L} \right) _{7,8}}\frac{1}{V_b-V_{GS5}}+2V_{TH} Vout1+Vout2=μnCox(LW)7,82IDVb−VGS51+2VTH
缺点:共模输出电平不是⾮常精准,受温度和⼯艺偏差的影响. -
另一种方法
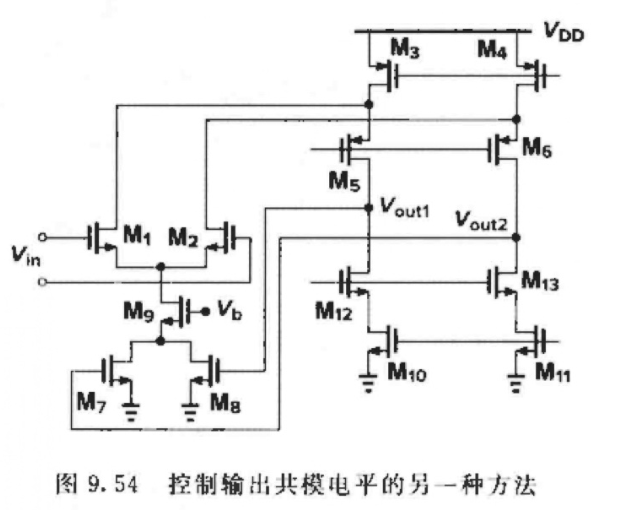
深线性区电阻CMFB技术调节输⼊:
∣ d V o u t , C M d V b ∣ c l o s e d ≈ V G S 7 , 8 − V T H 7 , 8 V D S 7 , 8 \left| \frac{\mathrm{d}V_{out,CM}}{\mathrm{d}V_{\mathrm{b}}} \right|_{c\mathrm{losed}}\approx \frac{V_{\mathrm{GS}7,8}-V_{\mathrm{TH}7,8}}{V_{\mathrm{DS}7,8}} ∣ ∣dVbdVout,CM∣ ∣closed≈VDS7,8VGS7,8−VTH7,8
缺点:为减⼩灵敏度,需要增⼤ VDS7,8,但以环路增益为代价。
9.7.4 两级运放中的CMFB
-
普通的两级运放
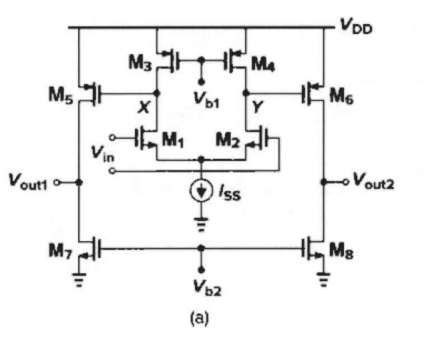
-
CMFB在第⼆级
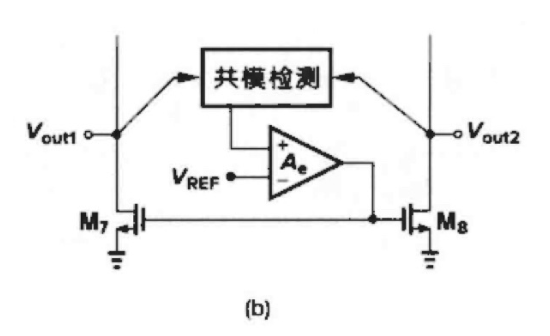
缺点:对第⼀级输出 X 和 Y 电平没有进⾏反馈控制, 不能保证所有的MOS管⼯作在饱和区
-
CMFB检测第⼆级CM电平,将结果返回到第⼀级
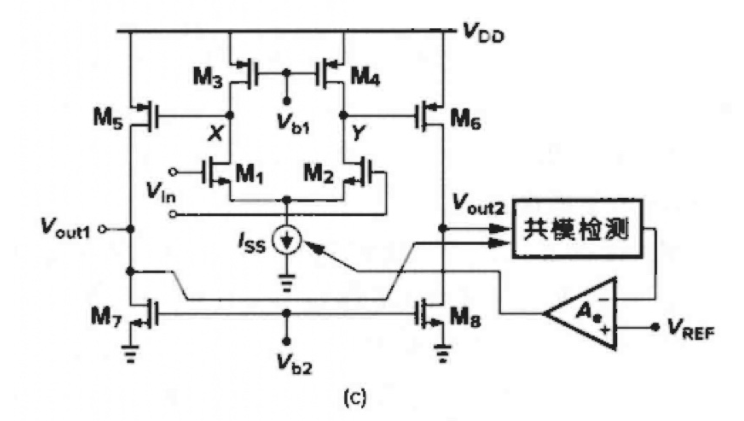
缺点:会引⼊多极点,影响系统的稳定性
改进:为运放的第⼀和第⼆级采⽤两个独⽴的CMFB
9.9 转换速率 (SR)
-
线性系统的对输⼊阶跃的响应
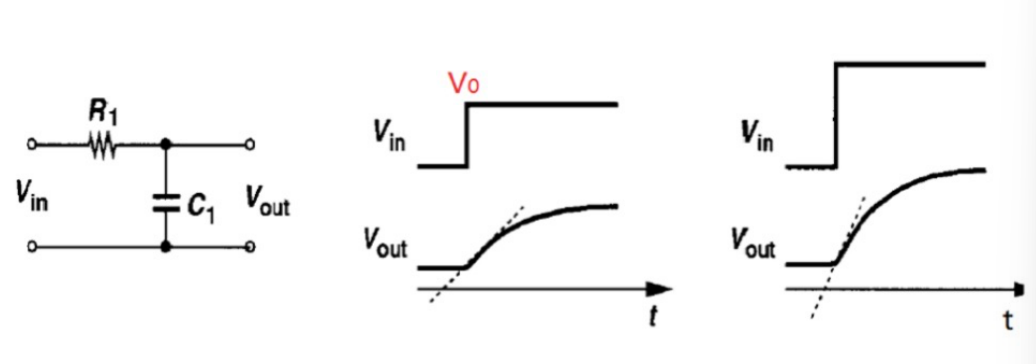
d V o u t d t = V 0 τ e − t τ ( t = 0 时得到斜率最大,称压摆率或转换速率) \frac{dV_{\mathrm{out}}}{dt}=\frac{V_0}{\tau}e^{\frac{-t}{\tau}} \\ \text{(}t=0\text{时得到斜率最大,称压摆率或转换速率)} dtdVout=τV0eτ−t(t=0时得到斜率最大,称压摆率或转换速率)
-
电路中的转换速率
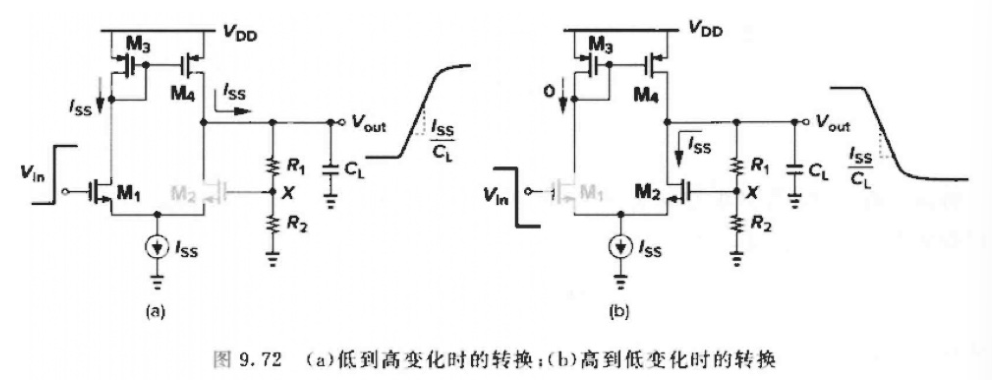
当输⼊由低到⾼时,是 M2 关断,M1, M3, M4 导通,产⽣斜率等于 I S S / C L I_{SS}/ C_L ISS/CL 的斜坡同理输⼊由⾼到低时,产⽣的斜率为负值。
I S S / C L I_{SS}/ C_L ISS/CL :流经 C L C_L CL 两端的电流为 I s s I_{ss} Iss,由 Δ Q = C Δ V = I Δ t (电容电压电流关系) \Delta Q=C\Delta V=I\Delta t\text{(电容电压电流关系)} ΔQ=CΔV=IΔt(电容电压电流关系),得到: Δ V Δ t = I C = I S S C L \frac{\Delta V}{\Delta t}=\frac{I}{C}=\frac{I_{SS}}{C_L} ΔtΔV=CI=CLISS
9.10 电源抑制PSRR
定义为:
P
S
R
R
=
∣
信号增益
电源到输出的增益
∣
PSRR = \left| \frac{\text{信号增益}}{\text{电源到输出的增益}} \right|
PSRR=∣
∣电源到输出的增益信号增益∣
∣
第十章 稳定性与频率补偿
10.1 概述
-
产⽣负反馈的条件
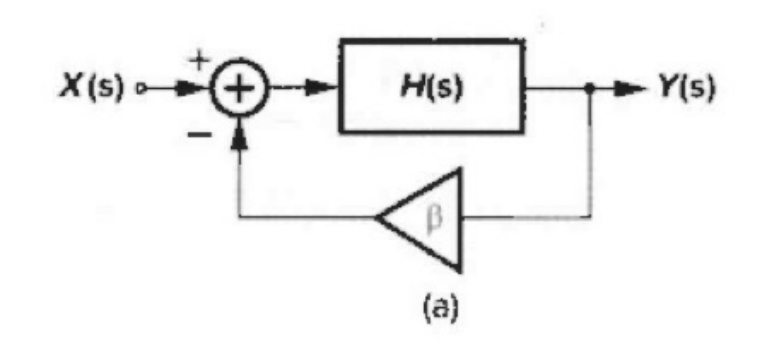
在基本负反馈系统中,产⽣负反馈的条件(巴克豪森判据):
∣ β H ( j ω 1 ) ∣ = 1 ∠ β H ( j ω 1 ) = − 18 0 ∘ \begin{aligned} &\left|\beta H\left(j \omega_{1}\right)\right|=1 \\ &\angle \beta H\left(j \omega_{1}\right)=-180^{\circ} \end{aligned} ∣βH(jω1)∣=1∠βH(jω1)=−180∘ -
增益交点和相位交点
-
增益交点GX频率:环路增益 β H = 1 ( 0 d B ) \beta \mathrm{H}=1(0 \mathrm{~dB}) βH=1(0 dB) 的频率。
-
增益交点PX频率: 环路相位 ∠ β H = − 18 0 ∘ \angle \beta H=-180^{\circ} ∠βH=−180∘ 对应的频率
-
稳定条件:增益交点 G X < G X< GX< 相位交点 P X P X PX ,其物理意义是在 P X P X PX 频率上, 环路增益<1, 反馈信号被缩小。

-
-
β \beta β与稳定性的关系
β 越小,环路增益越小, G X 越小,系统越稳定; 当电路为电压跟随器时 ( β = 1 , 此时 β 最大) , 系统稳定性最差。 \beta \text{越小,环路增益越小,}GX\text{越小,系统越稳定;} \\ \text{当电路为电压跟随器时} (\beta =1, \text{此时} \beta \,\,\text{最大)}, \text{系统稳定性最差。} β越小,环路增益越小,GX越小,系统越稳定;当电路为电压跟随器时(β=1,此时β最大),系统稳定性最差。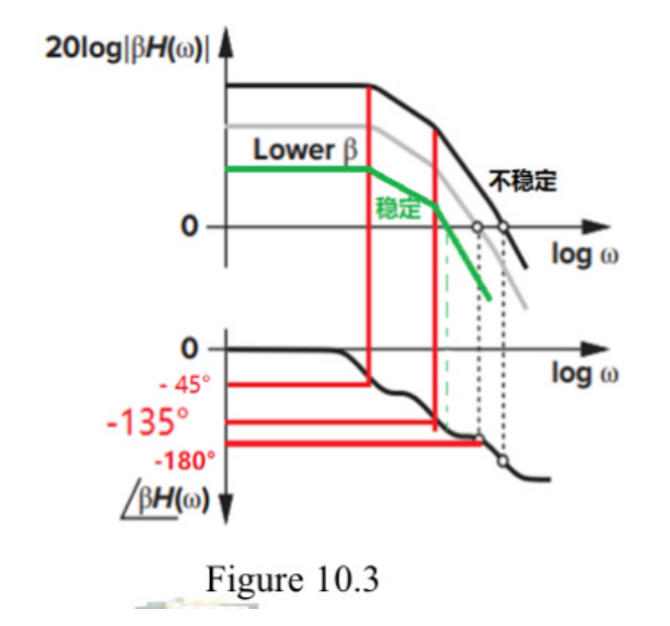
10.2 多极点系统(略)
10.3 相位裕度PM
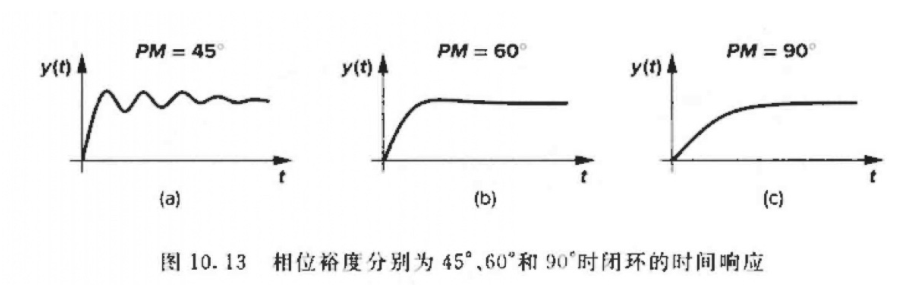
定义: P M = 180 ° + ∠ β H ( w = G X ) PM= 180°+ ∠βH(w= GX) PM=180°+∠βH(w=GX),即 180 180 180度加上增益交点频率对应的相移
当 P M = 60 ° PM= 60° PM=60°时为理想情况,对于更⼤的 P M PM PM,系统更稳定,但是时间响应减慢(信号带宽变⼩)
10.4 频率补偿基础
当电路有3个以上极点,需要考虑进⾏频率补偿,保证环路增益的 G X < P X GX< PX GX<PX。
10.5 两级运放的补偿(略)
10.6 两级运放的转换速率
-
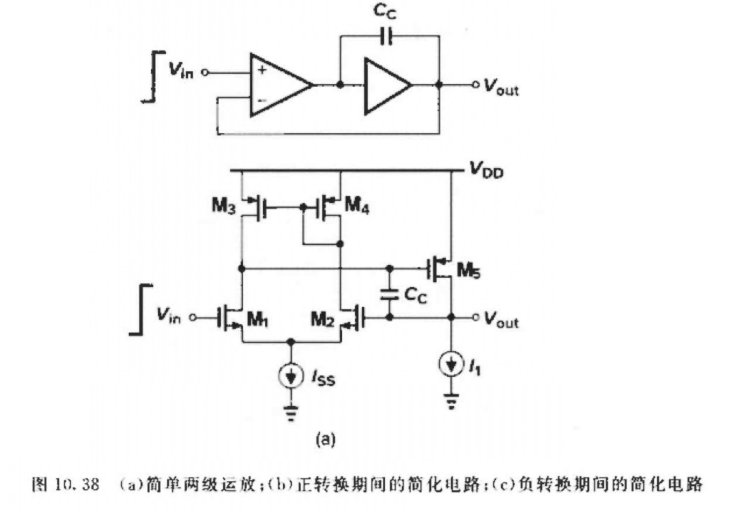
简单两级运放
-
正转换期间的简化电路
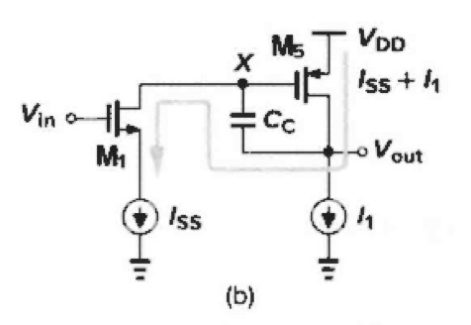
Vin 有⼀个⼤的正阶跃信号,M2、M4和M3均关断,此时 I S S I_{SS} ISS 对 C c C_c Cc 充电,转换速率为 I S S / C c I_{SS}/ C_c ISS/Cc。
-
负转换期间的简化电路
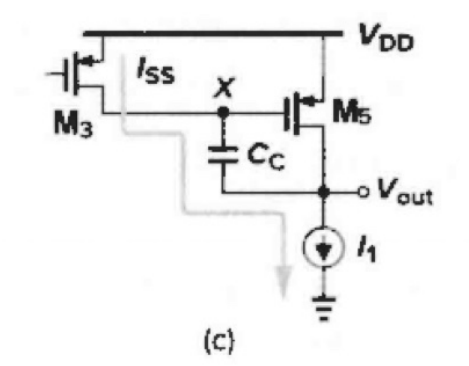
Vin 有⼀个⼤的负阶跃信号,M1 关断,M2 和 M4 省略没画,此时转换速率为 − I S S / C c - I_{SS}/ C_c −ISS/Cc。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








