百面机器学习之模型评估

1.准确率的局限性。

        Hulu 的奢侈品广告主们希望把广告定向投放给奢侈品用户。 Hulu 通过第三方的数据管理平台（Data Management Platform ， DMP ）拿到了一部分奢侈品用户的数据，并以此为训练集和测试集，训练和测试奢侈品用户的分类模型。该模型的分类准确率超过了95% ，但在实际广告投放过程中，该模型还是把大部分广告投给了非奢侈品用户，这可能是什么原因造成的？

在解答该问题之前，我们先回顾一下分类准确率的定义。准确率是指分类正确的样本占总样本个数的比例，即

其中 n correct 为被正确分类的样本个数， n total 为总样本的个数。

        准确率是分类问题中最简单也是最直观的评价指标，但存在明显的缺陷。比如，当负样本占99% 时，分类器把所有样本都预测为负样本也可以获得 99% 的准确率。所以，当不同类别的样本比例非常不均衡时，占比大的类别往往成为影响准确率的最主要因素。

        明确了这一点，这个问题也就迎刃而解了。显然，奢侈品用户只占 Hulu 全体用户的一小部分，虽然模型的整体分类准确率高，但是不代表对奢侈品用户的分类准确率也很高。在线上投放过程中，我们只会对模型判定的“ 奢侈品用户 ” 进行投放，因此，对“ 奢侈品用户 ” 判定的准确率不够高的问题就被放大了。为了解决这个问题，可以使用更为有效的平均准确率（每个类别下的样本准确率的算术平均）作为模型评估的指标。

        事实上，这是一道比较开放的问题，面试者可以根据遇到的问题一步步地排查原因。标准答案其实也不限于指标的选择，即使评估指标选择对了，仍会存在模型过拟合或欠拟合、测试集和训练集划分不合理、线下评估与线上测试的样本分布存在差异等一系列问题，但评估指标的选择是最容易被发现，也是最可能影响评估结果的因素。

2.精确率与召回率的权衡。

        Hulu 提供视频的模糊搜索功能，搜索排序模型返回的 Top 5 的精确率非常高，但在实际使用过程中，用户还是经常找不到想要的视频，特别是一些比较冷门的剧集，这可能是哪个环节出了问题呢？

        要回答这个问题，首先要明确两个概念，精确率和召回率。精确率是指分类正确的正样本个数占分类器判定为正样本的样本个数的比例。召回率是指分类正确的正样本个数占真正的正样本个数的比例。

        在排序问题中，通常没有一个确定的阈值把得到的结果直接判定为正样本或负样本，而是采用Top N返回结果的 Precision 值和 Recall 值来衡量排序模型的性能，即认为模型返回的Top N 的结果就是模型判定的正样本，然后计算前 N 个位置上的准确率Precision@N 和前 N 个位置上的召回率 Recall@N 。

        Precision 值和 Recall 值是既矛盾又统一的两个指标，为了提高 Precision 值，分类器需要尽量在“ 更有把握 ” 时才把样本预测为正样本，但此时往往会因为过于保守而漏掉很多“ 没有把握 ” 的正样本，导致 Recall 值降低。

        回到问题中来，模型返回的 Precision@5 的结果非常好，也就是说排序模型 Top5的返回值的质量是很高的。但在实际应用过程中，用户为了找一些冷门的视频， 往往会寻找排在较靠后位置的结果，甚至翻页去查找目标视频。但根据题目描述，用户经常找不到想要的视频，这说明模型没有把相关的视频都找出来呈现给用户。显然，问题出在召回率上。如果相关结果有100 个，即使 Precision@5 达到了100%， Recall@5 也仅仅是 5% 。在模型评估时，我们是否应该同时关注 Precision 值 和Recall 值？进一步而言，是否应该选取不同的 Top N 的结果进行观察呢？是否应

该选取更高阶的评估指标来更全面地反映模型在 Precision 值和 Recall 值两方面的表现？

        答案都是肯定的，为了综合评估一个排序模型的好坏，不仅要看模型在不同Top N下的 Precision@N 和 Recall@N ，而且最好绘制出模型的 P-R （ Precision-Recall）曲线。这里简单介绍一下 P-R 曲线的绘制方法。

        P-R 曲线的横轴是召回率，纵轴是精确率。对于一个排序模型来说，其 P-R 曲线上的一个点代表着，在某一阈值下，模型将大于该阈值的结果判定为正样本，小于该阈值的结果判定为负样本，此时返回结果对应的召回率和精确率。整条P-R曲线是通过将阈值从高到低移动而生成的。图2 是 P-R 曲线样例图，其中实线代表模型A 的 P-R 曲线，虚线代表模型 B 的 P-R 曲线。原点附近代表当阈值最大时模型的精确率和召回率。

 

图 2 P-R 曲线样例图

        由图可见，当召回率接近于 0 时，模型 A 的精确率为 0.9 ，模型 B 的精确率是 1 ，这说明模型B 得分前几位的样本全部是真正的正样本，而模型 A 即使得分最高的几个样本也存在预测错误的情况。并且，随着召回率的增加，精确率整体呈下降趋势。但是，当召回率为1 时，模型 A 的精确率反而超过了模型 B 。这充分说明，只用某个点对应的精确率和召回率是不能全面地衡量模型的性能，只有通过P-R 曲线的整体表现，才能够对模型进行更为全面的评估。

        除此之外， F1 score和 ROC 曲线也能综合地反映一个排序模型的性能。 F1 score是精准率和召回率的调和平均值，它定义为

3.平方根误差的“意外”。

        Hulu 作为一家流媒体公司，拥有众多的美剧资源，预测每部美剧的流量趋势对于广告投放、用户增长都非常重要。我们希望构建一个回归模型来预测某部美剧的流量趋势，但无论采用哪种回归模型，得到的RMSE 指标都非常高。然而事实是，模型在95% 的时间区间内的预测误差都小于 1% ，取得了相当不错的预测结果。那么，造成RMSE 指标居高不下的最可能的原因是什么？

        RMSE 经常被用来衡量回归模型的好坏，但按照题目的叙述， RMSE 这个指标却失效了。先看一下RMSE 的计算公式为

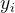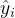其中， 是第 i 个样本点的真实值，是第 i 个样本点的预测值， n 是样本点的个数。

        一般情况下， RMSE 能够很好地反映回归模型预测值与真实值的偏离程度。但在实际问题中，如果存在个别偏离程度非常大的离群点（Outlier ）时，即使离群点数量非常少，也会让RMSE 指标变得很差。

        回到问题中来，模型在 95% 的时间区间内的预测误差都小于 1% ，这说明，在大部分时间区间内，模型的预测效果都是非常优秀的。然而，RMSE 却一直很差，这很可能是由于在其他的5% 时间区间内存在非常严重的离群点。事实上，在流量预估这个问题中，噪声点确实是很容易产生的，比如流量特别小的美剧、刚上映的美剧或者刚获奖的美剧，甚至一些相关社交媒体突发事件带来的流量，都可能会造成离群点。

        针对这个问题，有什么解决方案呢？可以从三个角度来思考。第一，如果我们认定这些离群点是“ 噪声点 ” 的话，就需要在数据预处理的阶段把这些噪声点过滤掉。第二，如果不认为这些离群点是“ 噪声点 ” 的话，就需要进一步提高模型的预测能力，将离群点产生的机制建模进去（这是一个宏大的话题，这里就不展开讨论了）。第三，可以找一个更合适的指标来评估该模型。关于评估指标，其实是存在比RMSE 的鲁棒性更好的指标，比如平均绝对百分比误差（ Mean Absolute

Percent Error ， MAPE ），它定义为

相比 RMSE ， MAPE 相当于把每个点的误差进行了归一化，降低了个别离群点带来的绝对误差的影响。

 

4.什么是ROC曲线？

        ROC 曲线是 Receiver Operating Characteristic Curve 的简称，中文名为 “ 受试者工作特征曲线” 。 ROC 曲线源于军事领域，而后在医学领域应用甚广， “ 受试者工作特征曲线” 这一名称也正是来自于医学领域。

        ROC 曲线的横坐标为假阳性率（ False Positive Rate ， FPR ）；纵坐标为真阳性率（True Positive Rate ， TPR ）。 FPR 和 TPR 的计算方法分别为

 

        上式中， P 是真实的正样本的数量， N 是真实的负样本的数量， TP 是 P 个正样本中被分类器预测为正样本的个数，FP 是 N 个负样本中被分类器预测为正样本的个数。

 

        只看定义确实有点绕，为了更直观地说明这个问题，我们举一个医院诊断病人的例子。假设有10 位疑似癌症患者，其中有 3 位很不幸确实患了癌症（ P =3 ），另外7 位不是癌症患者（ N =7 ）。医院对这 10 位疑似患者做了诊断，诊断出 3 位癌症患者，其中有2 位确实是真正的患者（ TP =2 ）。那么真阳性率 TPR = TP / P =2/3 。对于7 位非癌症患者来说，有一位很不幸被误诊为癌症患者（ FP =1 ），那么假阳性率 FPR = FP / N =1/7 。对于 “ 该医院 ” 这个分类器来说，这组分类结果就对应 ROC 曲线上的一个点（1/7 ， 2/3 ）。

 

5.如何绘制ROC曲线？

        事实上， ROC 曲线是通过不断移动分类器的 “ 截断点 ” 来生成曲线上的一组关键点的，通过下面的例子进一步来解释“ 截断点 ” 的概念。

 

        在二值分类问题中，模型的输出一般都是预测样本为正例的概率。假设测试集中有20 个样本，表 5 是模型的输出结果。样本按照预测概率从高到低排序。在输出最终的正例、负例之前，我们需要指定一个阈值，预测概率大于该阈值的样本会被判为正例，小于该阈值的样本则会被判为负例。比如，指定阈值为0.9 ，那么只有第一个样本会被预测为正例，其他全部都是负例。上面所说的“ 截断点 ” 指的就是区分正负预测结果的阈值。

        通过动态地调整截断点，从最高的得分开始（实际上是从正无穷开始，对应着ROC 曲线的零点），逐渐调整到最低得分，每一个截断点都会对应一个 FPR 和 TPR ，在 ROC 图上绘制出每个截断点对应的位置，再连接所有点就得到最终的ROC曲线。

表 5 二值分类模型的输出结果样例

就本例来说，当截断点选择为正无穷时，模型把全部样本预测为负例，那么FP 和 TP 必然都为 0 ， FPR 和 TPR 也都为 0 ，因此曲线的第一个点的坐标就是（0,0 ）。当把截断点调整为 0.9 时，模型预测 1 号样本为正样本，并且该样本确实是正样本，因此，TP =1 ， 20 个样本中，所有正例数量为 P =10 ，故TPR = TP / P =1/10 ；这里没有预测错的正样本，即 FP =0 ，负样本总数 N =10 ， 故FPR = FP / N =0/10=0 ，对应 ROC 曲线上的点（ 0,0.1 ）。依次调整截断点，直到画出全部的关键点，再连接关键点即得到最终的ROC 曲线，如图 5 所示。

 

图 5 ROC 曲线

        其实，还有一种更直观地绘制 ROC 曲线的方法。首先，根据样本标签统计出正负样本的数量，假设正样本数量为P ，负样本数量为 N ；接下来，把横轴的刻度间隔设置为1/ N ，纵轴的刻度间隔设置为 1/ P ；再根据模型输出的预测概率对样本进行排序（从高到低）；依次遍历样本，同时从零点开始绘制ROC 曲线，每遇到一个正样本就沿纵轴方向绘制一个刻度间隔的曲线，每遇到一个负样本就沿横轴方向绘制一个刻度间隔的曲线，直到遍历完所有样本，曲线最终停在（1,1 ）这个点，整个ROC 曲线绘制完成。

6.如何计算AUC？

        顾名思义， AUC 指的是 ROC 曲线下的面积大小，该值能够量化地反映基于ROC曲线衡量出的模型性能。计算 AUC 值只需要沿着 ROC 横轴做积分就可以了。由于ROC 曲线一般都处于 y = x 这条直线的上方（如果不是的话，只要把模型预测的概率反转成1− p 就可以得到一个更好的分类器），所以 AUC 的取值一般在 0.5 ～ 1 之间。AUC 越大，说明分类器越可能把真正的正样本排在前面，分类性能越好。

 

7.ROC曲线相比P-R曲线有什么特点？

        相比P-R曲线， ROC 曲线有一个特点，当正负样本的分布发生变化时， ROC 曲线的形状能够基本保持不变，而P-R 曲线的形状一般会发生较剧烈的变化。

        举例来说，图 7 是 ROC 曲线和 P-R 曲线的对比图，其中图 7 （ a ）和图7（ c ）是 ROC 曲线，图 7 （ b ）和图 7 （ d ）是 P-R 曲线，图 7 （ c ）和图7（ d ）则是将测试集中的负样本数量增加 10 倍后的曲线图。

 

图 7 ROC 曲线和 P-R 曲线的对比

 

        可以看出， P-R 曲线发生了明显的变化，而 ROC 曲线形状基本不变。这个特点让ROC 曲线能够尽量降低不同测试集带来的干扰，更加客观地衡量模型本身的性能。这有什么实际意义呢？在很多实际问题中，正负样本数量往往很不均衡。比如，计算广告领域经常涉及转化率模型，正样本的数量往往是负样本数量的1/1000甚至1/10000 。若选择不同的测试集， P-R 曲线的变化就会非常大，而 ROC 曲线则能够更加稳定地反映模型本身的好坏。所以，ROC 曲线的适用场景更多，被广泛用于排序、推荐、广告等领域。但需要注意的是，选择P-R 曲线还是 ROC 曲线是因实际问题而异的，如果研究者希望更多地看到模型在特定数据集上的表现，P-R 曲线则能够更直观地反映其性能。

 

8.结合你的学习和研究经历，探讨为什么在一些场景中要使用余弦相似度而不是欧氏距离？

        对于两个向量 A 和 B ，其余弦相似度定义为

，即两个向量夹角的余弦，关注的是向量之间的角度关系，并不关心它们的绝对大小，其取值

范围是 [−1,1] 。当一对文本相似度的长度差距很大、但内容相近时，如果使用词频或词向量作为特征，它们在特征空间中的的欧氏距离通常很大；而如果使用余弦相似度的话，它们之间的夹角可能很小，因而相似度高。此外，在文本、图像、视频等领域，研究的对象的特征维度往往很高，余弦相似度在高维情况下依然保持“ 相同时为 1 ，正交时为 0 ，相反时为 −1” 的性质，而欧氏距离的数值则受维度的影响，范围不固定，并且含义也比较模糊。

 

        在一些场景，例如 Word2Vec 中，其向量的模长是经过归一化的，此时欧氏距离与余弦距离有着单调的关系，即

 

        其中 || A − B || 2 表示欧氏距离， cos( A , B ) 表示余弦相似度， (1−cos( A , B )) 表示余弦距离。在此场景下，如果选择距离最小（相似度最大）的近邻，那么使用余弦相似度和欧氏距离的结果是相同的。

        总体来说，欧氏距离体现数值上的绝对差异，而余弦距离体现方向上的相对差异。例如，统计两部剧的用户观看行为，用户A 的观看向量为 (0,1) ，用户 B 为(1,0)；此时二者的余弦距离很大，而欧氏距离很小；我们分析两个用户对于不同视频的偏好，更关注相对差异，显然应当使用余弦距离。而当我们分析用户活跃度，以登陆次数( 单位：次 ) 和平均观看时长 ( 单位：分钟 ) 作为特征时，余弦距离会认为(1,10) 、 (10,100) 两个用户距离很近；但显然这两个用户活跃度是有着极大差异的，此时我们更关注数值绝对差异，应当使用欧氏距离。

 

9.在对模型进行过充分的离线评估之后，为什么还要进行在线A/B测试？

需要进行在线 A/B 测试的原因如下。

    （ 1 ）离线评估无法完全消除模型过拟合的影响，因此，得出的离线评估结果无法完全替代线上评估结果。

    （ 2 ）离线评估无法完全还原线上的工程环境。一般来讲，离线评估往往不会考虑线上环境的延迟、数据丢失、标签数据缺失等情况。因此，离线评估的结果是理想工程环境下的结果。

    （ 3 ）线上系统的某些商业指标在离线评估中无法计算。离线评估一般是针对模型本身进行评估，而与模型相关的其他指标，特别是商业指标，往往无法直接获得。比如，上线了新的推荐算法，离线评估往往关注的是ROC 曲线、 P-R 曲线等的改进，而线上评估可以全面了解该推荐算法带来的用户点击率、留存时长、PV访问量等的变化。这些都要由A/B 测试来进行全面的评估。

 

10.如何进行线上A/B测试？

       进行 A/B 测试的主要手段是进行用户分桶，即将用户分成实验组和对照组，对实验组的用户施以新模型，对对照组的用户施以旧模型。在分桶的过程中，要注意样本的独立性和采样方式的无偏性，确保同一个用户每次只能分到同一个桶中，在分桶过程中所选取的user_id 需要是一个随机数，这样才能保证桶中的样本是无偏的。

 

11.在模型评估过程中，有哪些主要的验证方法，它们的优缺点是什么?

■ Holdout 检验

        Holdout 检验是最简单也是最直接的验证方法，它将原始的样本集合随机划分成训练集和验证集两部分。比方说，对于一个点击率预测模型，我们把样本按照70%～ 30% 的比例分成两部分， 70% 的样本用于模型训练； 30% 的样本用于模型验证，包括绘制ROC 曲线、计算精确率和召回率等指标来评估模型性能。Holdout 检验的缺点很明显，即在验证集上计算出来的最后评估指标与原始分组有很大关系。为了消除随机性，研究者们引入了“ 交叉检验 ” 的思想。

 

■ 交叉检验

        k-fold 交叉验证：首先将全部样本划分成 k 个大小相等的样本子集；依次遍历这k 个子集，每次把当前子集作为验证集，其余所有子集作为训练集，进行模型的训练和评估；最后把k 次评估指标的平均值作为最终的评估指标。在实际实验中，k 经常取 10 。

        留一验证：每次留下 1 个样本作为验证集，其余所有样本作为测试集。样本总数为n，依次对 n 个样本进行遍历，进行 n 次验证，再将评估指标求平均值得到最终的评估指标。在样本总数较多的情况下，留一验证法的时间开销极大。事实上，留一验证是留p 验证的特例。留 p 验证是每次留下 p 个样本作为验证集，而从 n 个元素中选择p 个元素有种可能，因此它的时间开销更是远远高于留一验证，故而很少在实际工程中被应用。

 

■ 自助法

        不管是 Holdout 检验还是交叉检验，都是基于划分训练集和测试集的方法进行模型评估的。然而，当样本规模比较小时，将样本集进行划分会让训练集进一步减小，这可能会影响模型训练效果。有没有能维持训练集样本规模的验证方法呢？自助法可以比较好地解决这个问题。

        自助法是基于自助采样法的检验方法。对于总数为 n 的样本集合，进行 n 次有放回的随机抽样，得到大小为n 的训练集。 n 次采样过程中，有的样本会被重复采样，有的样本没有被抽出过，将这些没有被抽出的样本作为验证集，进行模型验证，这就是自助法的验证过程。

 

12.在自助法的采样过程中，对n个样本进行n次自助抽样，当n趋于无穷大时,最终有多少数据从未被选择过？

因此，当样本数很大时，大约有 36.8% 的样本从未被选择过，可作为验证集。

 

13.超参数有哪些调优方法？

        为了进行超参数调优，我们一般会采用网格搜索、随机搜索、贝叶斯优化等算法。在具体介绍算法之前，需要明确超参数搜索算法一般包括哪几个要素。一是目标函数，即算法需要最大化/ 最小化的目标；二是搜索范围，一般通过上限和下限来确定；三是算法的其他参数，如搜索步长。

■ 网格搜索

        网格搜索可能是最简单、应用最广泛的超参数搜索算法，它通过查找搜索范围内的所有的点来确定最优值。如果采用较大的搜索范围以及较小的步长，网格搜索有很大概率找到全局最优值。然而，这种搜索方案十分消耗计算资源和时间，特别是需要调优的超参数比较多的时候。因此，在实际应用中，网格搜索法一般会先使用较广的搜索范围和较大的步长，来寻找全局最优值可能的位置；然后会逐渐缩小搜索范围和步长，来寻找更精确的最优值。这种操作方案可以降低所需的时间和计算量，但由于目标函数一般是非凸的，所以很可能会错过全局最优值。

 

■ 随机搜索

        随机搜索的思想与网格搜索比较相似，只是不再测试上界和下界之间的所有值，而是在搜索范围中随机选取样本点。它的理论依据是，如果样本点集足够大，那么通过随机采样也能大概率地找到全局最优值，或其近似值。随机搜索一般会比网格搜索要快一些，但是和网格搜索的快速版一样，它的结果也是没法保证的。

 

■ 贝叶斯优化算法

        贝叶斯优化算法在寻找最优最值参数时，采用了与网格搜索、随机搜索完全不同的方法。网格搜索和随机搜索在测试一个新点时，会忽略前一个点的信息；而贝叶斯优化算法则充分利用了之前的信息。贝叶斯优化算法通过对目标函数形状进行学习，找到使目标函数向全局最优值提升的参数。具体来说，它学习目标函数形状的方法是，首先根据先验分布，假设一个搜集函数；然后，每一次使用新的采样点来测试目标函数时，利用这个信息来更新目标函数的先验分布；最后，算法测试由后验分布给出的全局最值最可能出现的位置的点。对于贝叶斯优化算法，有一个需要注意的地方，一旦找到了一个局部最优值，它会在该区域不断采样，所以很容易陷入局部最优值。为了弥补这个缺陷，贝叶斯优化算法会在探索和利用之间找到一个平衡点，“ 探索 ” 就是在还未取样的区域获取采样点；而“ 利用 ” 则是根据后验分布在最可能出现全局最值的区域进行采样。

 

14.在模型评估过程中，过拟合和欠拟合具体是指什么现象？

        过拟合是指模型对于训练数据拟合呈过当的情况，反映到评估指标上，就是模型在训练集上的表现很好，但在测试集和新数据上的表现较差。欠拟合指的是模型在训练和预测时表现都不好的情况。图14 形象地描述了过拟合和欠拟合的区别。

 

图 14  欠拟合与过拟合

        可以看出，图 14 （ a ）是欠拟合的情况，拟合的黄线没有很好地捕捉到数据的特征，不能够很好地拟合数据。图14 （ c ）则是过拟合的情况，模型过于复杂，把噪声数据的特征也学习到模型中，导致模型泛化能力下降，在后期应用过程中很容易输出错误的预测结果。

 

15.能否说出几种降低过拟合和欠拟合风险的方法？

■ 降低 “ 过拟合 ” 风险的方法

    （ 1 ）从数据入手，获得更多的训练数据。使用更多的训练数据是解决过拟合问题最有效的手段，因为更多的样本能够让模型学习到更多更有效的特征，减小噪声的影响。当然，直接增加实验数据一般是很困难的，但是可以通过一定的规则来扩充训练数据。比如，在图像分类的问题上，可以通过图像的平移、旋转、缩放等方式扩充数据；更进一步地，可以使用生成式对抗网络来合成大量的新训练数据。

    （ 2 ）降低模型复杂度。在数据较少时，模型过于复杂是产生过拟合的主要因素，适当降低模型复杂度可以避免模型拟合过多的采样噪声。例如，在神经网络模型中减少网络层数、神经元个数等；在决策树模型中降低树的深度、进行剪枝等。

    （ 3 ）正则化方法。给模型的参数加上一定的正则约束，比如将权值的大小加入到损失函数中。以L2 正则化为例：

这样，在优化原来的目标函数 C 0 的同时，也能避免权值过大带来的过拟合风险。

    （ 4 ）集成学习方法。集成学习是把多个模型集成在一起，来降低单一模型的过拟合风险，如Bagging 方法。

 

■ 降低 “ 欠拟合 ” 风险的方法

    （ 1 ）添加新特征。当特征不足或者现有特征与样本标签的相关性不强时，模型容易出现欠拟合。通过挖掘“ 上下文特征 ”“ID 类特征 ”“ 组合特征 ” 等新的特征，往往能够取得更好的效果。在深度学习潮流中，有很多模型可以帮助完成特征工程，如因子分解机、梯度提升决策树、Deep-crossing 等都可以成为丰富特征的方法。

    （ 2 ）增加模型复杂度。简单模型的学习能力较差，通过增加模型的复杂度可以使模型拥有更强的拟合能力。例如，在线性模型中添加高次项，在神经网络模型中增加网络层数或神经元个数等。

    （ 3 ）减小正则化系数。正则化是用来防止过拟合的，但当模型出现欠拟合现象时，则需要有针对性地减小正则化系数。