123 买卖股票的最佳时机III

123 买卖股票的最佳时机III

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入：prices = [3,3,5,0,0,3,1,4]
输出：6
解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。
     随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

示例 2：
输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。   
     注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。   
     因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3：

输入：prices = [7,6,4,3,1] 
输出：0 
解释：在这个情况下, 没有交易完成, 所以最大利润为 0。

示例 4：

输入：prices = [1]
输出：0

提示：

• 1 <= prices.length <= 10^5
• 0 <= prices[i] <= 10^5

思路

关键在于至多买卖两次，这意味着可以买卖一次，可以买卖两次，也可以不买卖。

接来下用动态规划五部曲详细分析一下：

1. 确定dp数组以及下标的含义

一天一共就有五个状态，

1. 没有操作 （其实也可以不设置这个状态）
2. 第一次持有股票
3. 第一次不持有股票
4. 第二次持有股票
5. 第二次不持有股票

dp[i] [j]中 i表示第i天，j为 [0 - 4] 五个状态，dp[i] [j]表示第i天状态j所剩最大现金。

需要注意：dp[i] [1]，表示的是第i天，买入股票的状态，并不是说一定要第i天买入股票，这是容易陷入的误区。

例如 dp[i] [1] ，并不是说 第i天一定买入股票，有可能 第 i-1天 就买入了，那么 dp[i] [1] 延续买入股票的这个状态。

2. 确定递推公式

达到dp[i] [1]状态，有两个具体操作：

• 操作一：第i天买入股票了，那么dp[i] [1] = dp[i-1] [0] - prices[i]
• 操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i] [1] = dp[i - 1] [1]

那么dp[i] [1]究竟选 dp[i-1] [0] - prices[i]，还是dp[i - 1] [1]呢？

一定是选最大的，所以 dp[i][1] = max(dp[i-1] [0] - prices[i], dp[i - 1] [1]);

同理dp[i] [2]也有两个操作：

• 操作一：第i天卖出股票了，那么dp[i] [2] = dp[i - 1] [1] + prices[i]
• 操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i] [2] = dp[i - 1] [2]

所以dp[i][2] = max(dp[i - 1] [1] + prices[i], dp[i - 1] [2])

同理可推出剩下状态部分：

dp[i] [3] = max(dp[i - 1] [3], dp[i - 1] [2] - prices[i]);

dp[i] [4] = max(dp[i - 1] [4], dp[i - 1] [3] + prices[i]);

3. dp数组如何初始化

第0天没有操作，这个最容易想到，就是0，即：dp[0] [0] = 0;

第0天做第一次买入的操作，dp[0] [1] = -prices[0];

第0天做第一次卖出的操作，这个初始值应该是多少呢？

此时还没有买入，怎么就卖出呢？ 其实可以理解当天买入，当天卖出，所以dp[0] [2] = 0;

第0天第二次买入操作，初始值应该是多少呢？第一次还没买入呢，怎么初始化第二次买入呢？

第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后再买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。

所以第二次买入操作，初始化为：dp[0] [3] = -prices[0];

同理第二次卖出初始化dp[0] [4] = 0;

4. 确定遍历顺序

从递归公式其实已经可以看出，一定是从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值。

5. 举例推导dp数组

以输入[1,2,3,4,5]为例

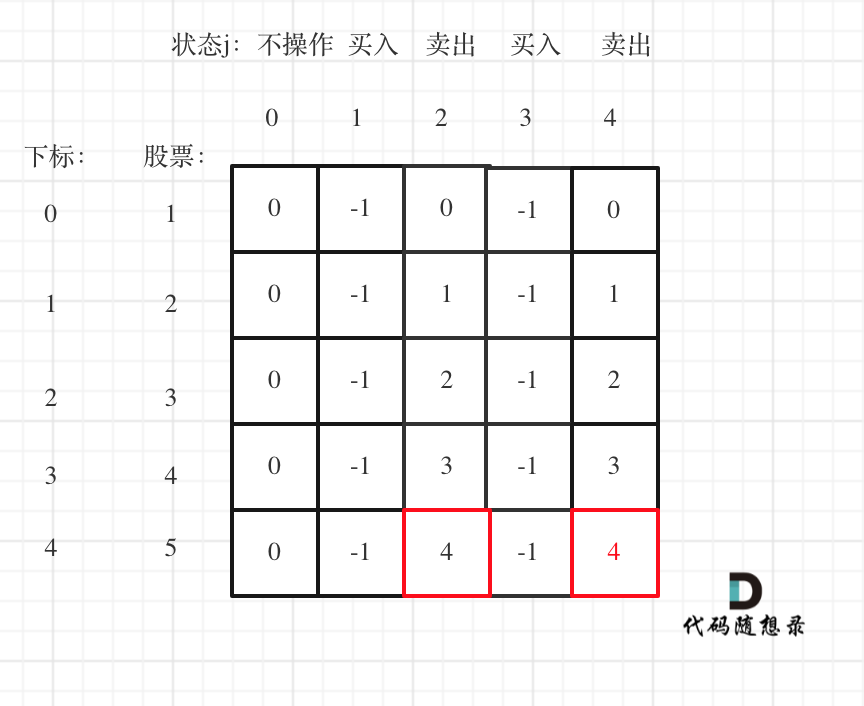
可以看到红色框为最后两次卖出的状态。

如果第一次卖出已经是最大值了，那么我们可以在当天立刻买入再立刻卖出。所以dp[4] [4]已经包含了dp[4] [2]的情况。也就是说第二次卖出手里所剩的钱一定是最多的。

代码如下：

• 时间复杂度：O(n)
• 空间复杂度：O(n × 5)

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.size() == 0) return 0;
        vector<vector<int>> dp(prices.size(), vector<int>(5, 0));
        dp[0][1] = -prices[0];
        dp[0][3] = -prices[0];
        for (int i = 1; i < prices.size(); i++) {
            dp[i][0] = dp[i - 1][0];
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        return dp[prices.size() - 1][4];
    }
};

其实可以不设置，‘0. 没有操作’ 这个状态，因为没有操作，手上的现金自然就是0， 正如在 121.买卖股票的最佳时机和 122.买卖股票的最佳时机II也没有设置这一状态是一样的。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if (prices.size() == 0) return 0;
        vector<vector<int>> dp(prices.size(), vector<int>(5, 0));
        dp[0][1] = -prices[0];
        dp[0][3] = -prices[0];
        for (int i = 1; i < prices.size(); i++) {
            dp[i][1] = max(dp[i - 1][1], 0 - prices[i]);
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        return dp[prices.size() - 1][4];
    }
};