pytorch
预备知识
数据操作
张量
张量表示由一个数值组成的数组,这个数组可能有多个维度,具有一个轴的张量对应数学上的向量(vector); 具有两个轴的张量对应数学上的矩阵(matrix); 具有两个轴以上的张量没有特殊的数学名称。
- 可以使用arange创建向量,向量的范围是[0,num)
x=torch.arange(10)
#tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
- 可以通过张量的
shape属性访问张量的形状
x.shape
#torch.Size([10])
- 查看张量中元素的总数
x.numel()
#10
- 改变张量的形状
X=x.reshape(3,4)
#tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
我们可以通过-1来调用此自动计算出维度的功能。 即我们可以用x.reshape(-1,4)或x.reshape(3,-1)来取代
- 初始化矩阵
torch.zeros((2, 3, 4))
torch.ones((2, 3, 4))
随机初始化张量。其中的每个元素都从均值为0、标准差为1的标准高斯分布(正态分布)中随机采样。
torch.randn(3, 4)
通过提供包含数值的Python列表(或嵌套列表),来为所需张量中的每个元素赋予确定值。 在这里,最外层的列表对应于轴0,内层的列表对应于轴1。
torch.tensor([[2, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
运算符
x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
x + y, x - y, x * y, x / y, x ** y
# **运算符是求幂运算
(tensor([ 3., 4., 6., 10.]),
tensor([-1., 0., 2., 6.]),
tensor([ 2., 4., 8., 16.]),
tensor([0.5000, 1.0000, 2.0000, 4.0000]),
tensor([ 1., 4., 16., 64.]))
- 把多个张量连结(concatenate)在一起。需要提供张量列表,并给出沿哪个轴连结
0是按行,1是按列
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
torch.cat((X,Y),dim=0)
'''
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[ 2., 1., 4., 3.],
[ 1., 2., 3., 4.],
[ 4., 3., 2., 1.]])
'''
torch.cat((X,Y),dim=1)
'''
tensor([[ 0., 1., 2., 3., 2., 1., 4., 3.],
[ 4., 5., 6., 7., 1., 2., 3., 4.],
[ 8., 9., 10., 11., 4., 3., 2., 1.]])
'''
- 对张量中所有元素求和
X.sum() - 广播机制:由于
a和b分别是3×1和1×2矩阵,如果让它们相加,它们的形状不匹配。 我们将两个矩阵广播为一个更大的3×2矩阵,如下所示:矩阵a将复制列, 矩阵b将复制行,然后再按元素相加。
a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))
a+b
'''
(tensor([[0],
[1],
[2]]),
tensor([[0, 1]]))
'''
- 可以用
[-1]选择最后一个元素,可以用[1:3]选择第二个和第三个元素
X[-1], X[1:3]
(tensor([ 8., 9., 10., 11.]),
tensor([[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]]))
我们还可以通过指定索引来将元素写入矩阵
X[1,2]=90
执行原地操作非常简单。 我们可以使用切片表示法将操作的结果分配给先前分配的数组
可以使用X[:] = X + Y或X += Y来减少操作的内存开销。
before = id(X)
X += Y
id(X) == before
- 转化类型
张量转换为NumPy张量(ndarray)
A = X.numpy()
B = torch.tensor(A)
要将大小为1的张量转换为Python标量,我们可以调用item函数或Python的内置函数。
a = torch.tensor([3.5])
a, a.item(), float(a), int(a)
- 处理缺失值
inputs = inputs.fillna(inputs.mean())
巷子类型为“Pave”的行会将“Alley_Pave”的值设置为1,“Alley_nan”的值设置为0。
pd.get_dummies相当于onehot编码,常用与把离散的类别信息转化为onehot编码形式。
inputs = pd.get_dummies(inputs, dummy_na=True)
'''
NumRooms Alley_Pave Alley_nan
0 3.0 1 0
1 2.0 0 1
2 4.0 0 1
3 3.0 0 1
'''
线性代数
标量由只有一个元素的张量表示。
矩阵的转置X.T
图像以n维数组形式出现, 其中3个轴对应于高度、宽度,以及一个通道(channel)轴, 用于表示颜色通道(红色、绿色和蓝色)。
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone() # 通过分配新内存,将A的一个副本分配给B
降维求和
张量每一行求和X.sum(axis=0)
求平均值A.mean(), A.sum() / A.numel()
非降维求和
sum_A = A.sum(axis=1, keepdims=True)
#沿行方向累积求和
A.cumsum(axis=0)
tensor([[ 0., 1., 2., 3.],
[ 4., 6., 8., 10.],
[12., 15., 18., 21.],
[24., 28., 32., 36.],
[40., 45., 50., 55.]])
点积
# 点积,相同位置的按元素乘积的和
torch.dot(x, y)
# 矩阵-向量积
torch.mv(A, x)
# 矩阵乘法
torch.mm(A, B)
范数
一个向量的范数告诉我们一个向量有多大
L2范数(默认)

u = torch.tensor([3.0, -4.0])
torch.norm(u) #tensor(5.)
L1范数

torch.abs(u).sum()
Frobenius范数(Frobenius norm)是矩阵元素平方和的平方根:

a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
概率
机器学习就是做出预测
# 得到每种情况出现的次数
#multinomial.Multinomial(试验次数, 事件概率).sample((实验组数,))
multinomial.Multinomial(10000, fair_probs).sample((5,))
multinomial.Multinomial(10, fair_probs).sample((5,))
# 进行500组实验,每组抽取10个样本。模拟骰子
counts = multinomial.Multinomial(10, fair_probs).sample((500,))
cum_counts = counts.cumsum(dim=0)
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)
d2l.set_figsize((6, 4.5))
for i in range(6):
d2l.plt.plot(estimates[:, i].numpy(),
label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend();

线性神经网络
损失函数
平方误差函数

为了度量模型在整个数据集上的质量,我们需计算在训练集n个样本上的损失均值

在模型训练时寻找参数(w,b),使得训练样本的总损失最小化
随机梯度下降
梯度下降最简单的用法是计算损失函数(数据集中所有样本的损失均值) 关于模型参数的导数(在这里也可以称为梯度)。 但实际中的执行可能会非常慢:因为在每一次更新参数之前,我们必须遍历整个数据集。 因此,我们通常会在每次需要计算更新的时候随机抽取一小批样本, 这种变体叫做小批量随机梯度下降(minibatch stochastic gradient descent)。
算法的步骤如下:(1)初始化模型参数的值,如随机初始化;
(2)从数据集中随机抽取小批量样本且在负梯度的方向上更新参数,并不断迭代这一步骤。
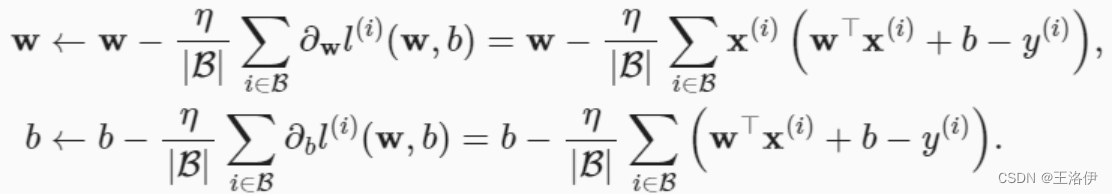
|B|表示每个小批量中的样本数,这也称为批量大小(batch size)。 η表示学习率(learning rate)。
- 对于线性回归,每个输入都与每个输出(在本例中只有一个输出)相连, 我们将这种变换称为全连接层(fully-connected layer)或称为稠密层(dense layer)
def sgd(params, lr, batch_size):
"""小批量随机梯度下降"""
with torch.no_grad():
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_() # “清除”x的梯度值
线性回归
神经网络的训练有时候可能希望保持一部分的网络参数不变,只对其中一部分的参数进行调整。或者训练部分分支网络,并不让其梯度对主网络的梯度造成影响.这时候我们就需要使用detach()函数来切断一些分支的反向传播.
tensor.detach()返回一个新的tensor,从当前计算图中分离下来。但是仍指向原变量的存放位置,不同之处只是requirse_grad为false.得到的这个tensor永远不需要计算器梯度,不具有grad.即使之后重新将它的requires_grad置为true,它也不会具有梯度grad.这样我们就会继续使用这个新的tensor进行计算,后面当我们进行反向传播时,到该调用detach()的tensor就会停止,不能再继续向前进行传播.
使用detach返回的tensor和原始的tensor共同一个内存,即一个修改另一个也会跟着改变.
no_grad与detach有异曲同工之妙,都是逃避autograd的追踪。
yield和return的关系和区别了,带yield的函数是一个生成器,而不是一个函数了,这个生成器有一个函数就是next函数,next就相当于“下一步”生成哪个数,这一次的next开始的地方是接着上一次的next停止的地方执行的,所以调用next的时候,生成器并不会从foo函数的开始执行,只是接着上一步停止的地方开始,然后遇到yield后,return出要生成的数,此步就结束。
def linreg(X, w, b):
"""线性回归模型"""
return torch.matmul(X, w) + b
训练
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # X和y的小批量损失
# 因为l形状是(batch_size,1),而不是一个标量。l中的所有元素被加到一起,
# 并以此计算关于[w,b]的梯度
l.sum().backward()
sgd([w, b], lr, batch_size) # 使用参数的梯度更新参数
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
线性神经网络
from torch import nn
#nn.Linear(输入特征形状,输出特征形状)
net = nn.Sequential(nn.Linear(2, 1))
# 初始化模型参数
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)
# 定义损失函数,均方误差
loss = nn.MSELoss()
# 定义优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.03)
# 训练
num_epochs = 3
for epoch in range(num_epochs):
for X, y in data_iter:
l = loss(net(X) ,y)
trainer.zero_grad()
l.backward()
trainer.step()
l = loss(net(features), labels)
print(f'epoch {epoch + 1}, loss {l:f}')
softmax回归
Softmax函数就可以将多分类的输出值转换为范围在***[0, 1]***和为1的概率分布。
softmax函数
s
o
f
t
m
a
x
(
X
)
i
j
=
exp
(
X
i
j
)
∑
k
exp
(
X
i
k
)
.
\mathrm{softmax}(\mathbf{X})_{ij} = \frac{\exp(\mathbf{X}_{ij})}{\sum_k \exp(\mathbf{X}_{ik})}.
softmax(X)ij=∑kexp(Xik)exp(Xij).
交叉熵损失函数为
l
(
y
,
y
^
)
=
−
∑
j
=
1
q
y
j
log
y
j
^
l(y,\hat{y} )= \mathrm{-}\sum_{j=1}^q y_j\log \hat{y_j}
l(y,y^)=−j=1∑qyjlogyj^
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater): #@save
"""训练模型(定义见第3章)"""
animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
legend=['train loss', 'train acc', 'test acc'])
for epoch in range(num_epochs):
train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
test_acc = evaluate_accuracy(net, test_iter)
animator.add(epoch + 1, train_metrics + (test_acc,))
train_loss, train_acc = train_metrics
assert train_loss < 0.5, train_loss
assert train_acc <= 1 and train_acc > 0.7, train_acc
assert test_acc <= 1 and test_acc > 0.7, test_acc
# 初始化参数模型
# PyTorch不会隐式地调整输入的形状。因此,
# 我们在线性层前定义了展平层(flatten),来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
# 损失函数
loss = nn.CrossEntropyLoss(reduction='none')
#优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.1)
#训练
num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
多层感知机
通过在网络中添加一个或多个隐藏层来克服线性模型的限制,使其能处理更普遍的函数关系模型。要做到这一点,最简单的方法是将许多全连接层堆叠在一起。每一层输出到上面的层,直到生成最后的输出。可以把前L-1层看作表示,把最后一层看作线性预测器,这种架构称为多层感知机(multilayer perceptron,MLP)
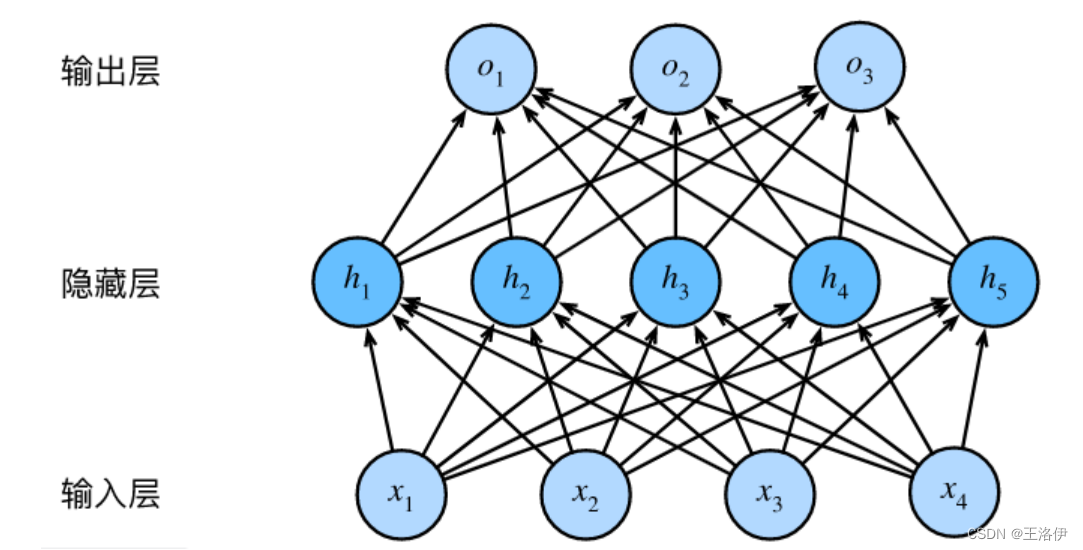
这个多层感知机有4个输入,3个输出,其隐藏层包含5个隐藏单元。 输入层不涉及任何计算,因此使用此网络产生输出只需要实现隐藏层和输出层的计算。 因此,这个多层感知机中的层数为2。
H
=
σ
(
X
W
(
1
)
+
b
(
1
)
)
,
O
=
H
W
(
2
)
+
b
(
2
)
.
\begin{aligned} \mathbf{H} & = \sigma(\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)}), \\ \mathbf{O} & = \mathbf{H}\mathbf{W}^{(2)} + \mathbf{b}^{(2)}.\\ \end{aligned}
HO=σ(XW(1)+b(1)),=HW(2)+b(2).
激活函数
激活函数(activation function)通过计算加权和并加上偏置来确定神经元是否应该被激活, 它们将输入信号转换为输出的可微运算。 大多数激活函数都是非线性的。
ReLU函数
修正线性单元(Rectified linear unit,ReLU)。实现简单,同时在各种预测任务中表现良好。它提供了一种非常简单的非线性变换。
R e L U ( x ) = m a x ( x , 0 ) ReLU(x)=max(x,0) ReLU(x)=max(x,0)
ReLU函数通过将相应的活性值设为0,仅保留正元素并丢弃所有负元素。当x特别大时也不会饱和。
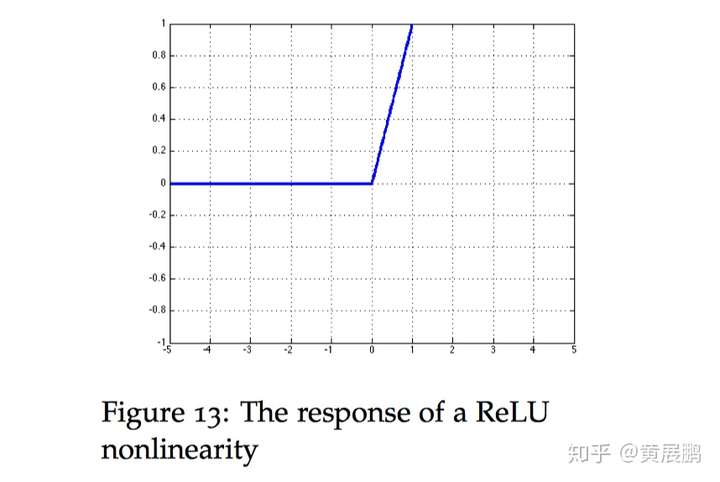
R
e
L
U
ReLU
ReLU 函数的微分是一个分段函数:
r
e
l
u
′
(
x
)
=
{
1
x
>
0
0
:
o
t
h
e
r
w
i
s
e
relu^\prime(x)=\begin{cases} 1&x>0\\ 0&:otherwise \end{cases}
relu′(x)={10x>0:otherwise
要么让参数消失,要么让参数通过。 这使得优化表现得更好,并且ReLU减轻了困扰以往神经网络的梯度消失问题.
ReLU变种
Leaky RelU:传统的ReLU 单元当 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-noO1HwfH-1670308960424)(https://www.zhihu.com/equation?tex=z)] 的值小于 0 时,是不会反向传播误差 改善了这一点,当 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rnEHtGdK-1670308960425)(https://www.zhihu.com/equation?tex=z)] 的值小于0时,仍然会有一个很小的误差反向传播回去。
其中0<k<1.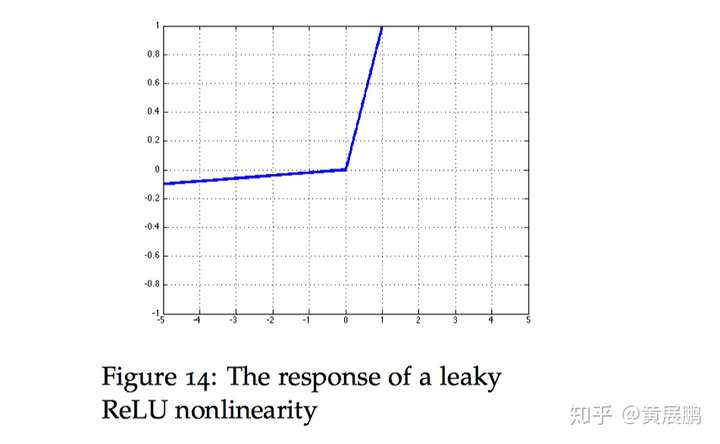
函数的微分是一个分段函数:
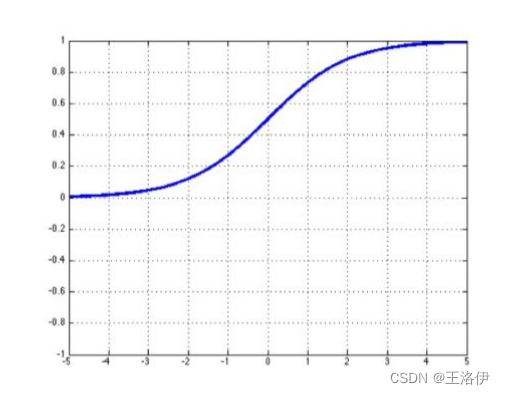
Sigmoid
对于一个定义域在ℝ中的输入, sigmoid函数将输入变换为区间(0, 1)上的输出。 因此,sigmoid通常称为挤压函数(squashing function): 它将范围(-inf, inf)中的任意输入压缩到区间(0, 1)中的某个值:
sigmoid ( x ) = 1 1 + exp ( − x ) . \operatorname{sigmoid}(x) = \frac{1}{1 + \exp(-x)}. sigmoid(x)=1+exp(−x)1.
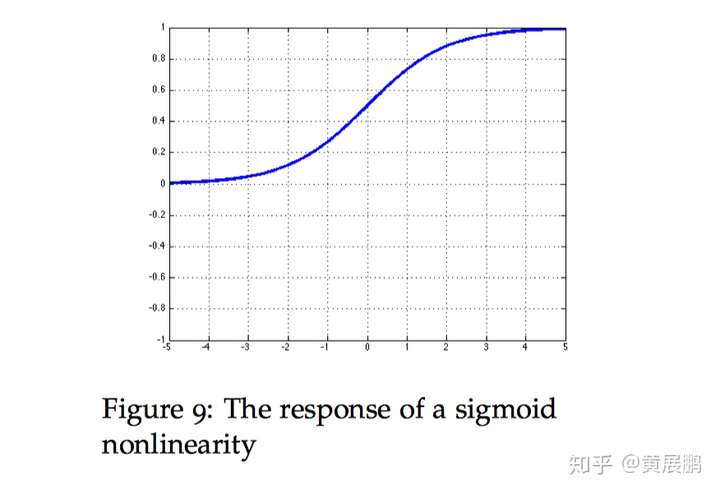
导数为:
d
d
x
sigmoid
(
x
)
=
exp
(
−
x
)
(
1
+
exp
(
−
x
)
)
2
=
sigmoid
(
x
)
(
1
−
sigmoid
(
x
)
)
.
\frac{d}{dx} \operatorname{sigmoid}(x) = \frac{\exp(-x)}{(1 + \exp(-x))^2} = \operatorname{sigmoid}(x)\left(1-\operatorname{sigmoid}(x)\right).
dxdsigmoid(x)=(1+exp(−x))2exp(−x)=sigmoid(x)(1−sigmoid(x)).
Tanh
tanh与sigmoid函数类似,tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上。
tanh函数的公式如下:
tanh ( x ) = 1 − exp ( − 2 x ) 1 + exp ( − 2 x ) . \operatorname{tanh}(x) = \frac{1 - \exp(-2x)}{1 + \exp(-2x)}. tanh(x)=1+exp(−2x)1−exp(−2x).
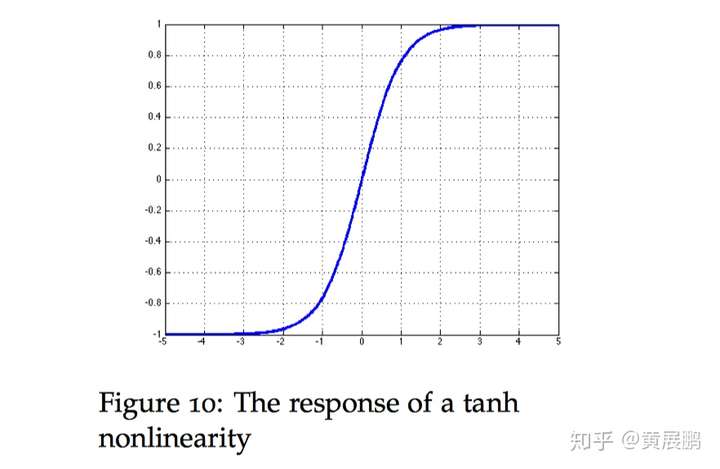
梯度为:
d d x tanh ( x ) = 1 − tanh 2 ( x ) . \frac{d}{dx} \operatorname{tanh}(x) = 1 - \operatorname{tanh}^2(x). dxdtanh(x)=1−tanh2(x).
Hard tanh:有时候 hard tanh 函数有时比 tanh 函数的选择更为优先,因为它的计算量更小。然而当 z 的值大于 1 时,函数的数值会饱和(如下图所示会恒等于 1)。tanh 激活函数为:
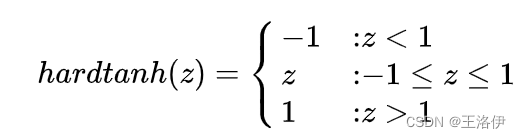
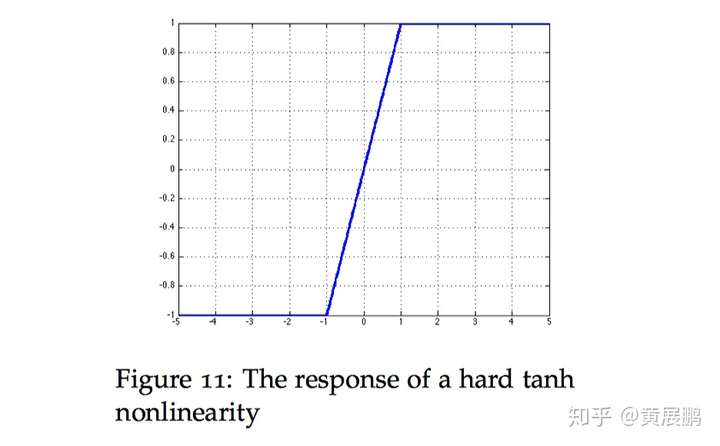
hard tanh这个函数的微分也可以用分段函数的形式表示:
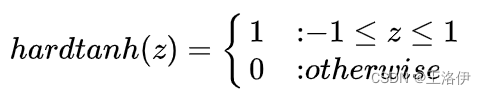
Soft sign: 是另外一种非线性激活函数,它可以是tanh 的另外一种选择,因为它 hard clipped functions 那样过早地饱和:
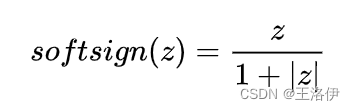
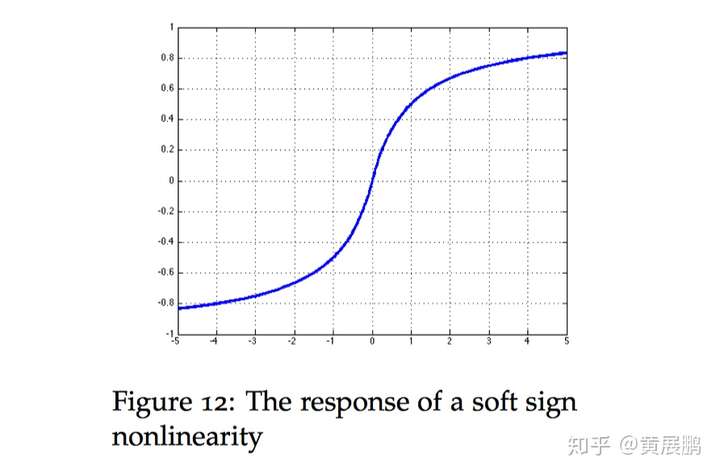
函数的微分表达式为:
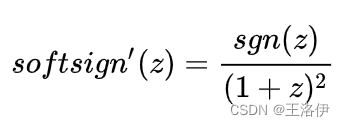
其中 sgn 是符号函数,根据 z 的符号返回 1 或者 -1 。
多层感知机简单实现
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)
模型选择
训练误差(training error)是指, 模型在训练数据集上计算得到的误差。 泛化误差(generalization error)是指, 模型应用在同样从原始样本的分布中抽取的无限多数据样本时,模型误差的期望。
影响模型泛化的因素:
- 可调整参数的数量。当可调整参数的数量(有时称为自由度)很大时,模型往往更容易过拟合。
- 参数采用的值。当权重的取值范围较大时,模型可能更容易过拟合。
- 训练样本的数量。即使你的模型很简单,也很容易过拟合只包含一两个样本的数据集。而过拟合一个有数百万个样本的数据集则需要一个极其灵活的模型。
除了训练和测试数据集之外,还增加一个验证数据集(validation dataset), 也叫验证集(validation set)
过拟合:训练误差明显低于验证误差
**欠拟合:**训练和验证误差之间的泛化误差很小
𝐾折交叉验证
当训练数据稀缺时,我们甚至可能无法提供足够的数据来构成一个合适的验证集。 这个问题的一个流行的解决方案是采用𝐾折交叉验证。 这里,原始训练数据被分成𝐾个不重叠的子集。 然后执行𝐾次模型训练和验证,每次在𝐾−1个子集上进行训练, 并在剩余的一个子集(在该轮中没有用于训练的子集)上进行验证。 最后,通过对𝐾次实验的结果取平均来估计训练和验证误差。
权重衰减
在训练参数化机器学习模型时, 权重衰减(weight decay)是最广泛使用的正则化的技术之一, 它通常也被称为 L 2 L_2 L2正则化。
一种简单的方法是通过线性函数 𝑓(𝐱)=𝐰⊤𝐱中的权重向量的某个范数来度量其复杂性。要保证权重向量比较小, 最常用方法是将其范数作为惩罚项加到最小化损失的问题中。 将原来的训练目标最小化训练标签上的预测损失, 调整为最小化预测损失和惩罚项之和。如果我们的权重向量增长的太大, 我们的学习算法可能会更集中于最小化权重范数 ∣ ∣ w ∣ ∣ 2 ||w||^2 ∣∣w∣∣2
使用 L 2 L_2 L2 范数的一个原因是它对权重向量的大分量施加了巨大的惩罚。 这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型。 在实践中,这可能使它们对单个变量中的观测误差更为稳定。 相比之下, L 1 L_1 L1 惩罚会导致模型将权重集中在一小部分特征上, 而将其他权重清除为零。 这称为特征选择(feature selection),这可能是其他场景下需要的。
原来的损失函数
L ( w , b ) = 1 n ∑ i = 1 n 1 2 ( w ⊤ x ( i ) + b − y ( i ) ) 2 . L(\mathbf{w}, b) = \frac{1}{n}\sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2. L(w,b)=n1i=1∑n21(w⊤x(i)+b−y(i))2.
回想一下,
x
(
i
)
\mathbf{x}^{(i)}
x(i)是样本
i
i
i的特征,
y
(
i
)
y^{(i)}
y(i)是样本
i
i
i的标签,
(
w
,
b
)
(\mathbf{w}, b)
(w,b)是权重和偏置参数。为了惩罚权重向量的大小,
我们必须以某种方式在损失函数中添加
∥
w
∥
2
\| \mathbf{w} \|^2
∥w∥2,但是模型应该如何平衡这个新的额外惩罚的损失?实际上,我们通过正则化常数
λ
\lambda
λ来描述这种权衡,这是一个非负超参数,我们使用验证数据拟合:
L ( w , b ) + λ 2 ∥ w ∥ 2 , L(\mathbf{w}, b) + \frac{\lambda}{2} \|\mathbf{w}\|^2, L(w,b)+2λ∥w∥2,
L 2 L_2 L2正则化回归的小批量随机梯度下降更新如下式:
w ← ( 1 − η λ ) w − η ∣ B ∣ ∑ i ∈ B x ( i ) ( w ⊤ x ( i ) + b − y ( i ) ) . \begin{aligned} \mathbf{w} & \leftarrow \left(1- \eta\lambda \right) \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right). \end{aligned} w←(1−ηλ)w−∣B∣ηi∈B∑x(i)(w⊤x(i)+b−y(i)).
dropout
使用 dropout 的方式是我们取每个神经元层的输出 h ,并保持概率 p 的神经元是激活的,否则将神经元设置为 0 。然后,在反向传播中我们仅对在前向传播中激活的神经元回传梯度。最后,在测试过程,我们使用神经网络中全部的神经元进行前向传播计算。然而,有一个关键的微妙之处,为了使 dropout 有效地工作,测试阶段的神经元的预期输出应与训练阶段大致相同-否则输出的大小可能会有很大的不同
暂退法在前向传播过程中,计算每一内部层的同时注入噪声,这已经成为训练神经网络的常用技术。 这种方法之所以被称为暂退法,因为我们从表面上看是在训练过程中丢弃(drop out)一些神经元。 在整个训练过程的每一次迭代中,标准暂退法包括在计算下一层之前将当前层中的一些节点置零。
当我们将暂退法应用到隐藏层,以 p p p的概率将隐藏单元置为零时,结果可以看作是一个只包含原始神经元子集的网络。比如,删除了 h 2 h_2 h2和 h 5 h_5 h5,因此输出的计算不再依赖于 h 2 h_2 h2或 h 5 h_5 h5,并且它们各自的梯度在执行反向传播时也会消失。这样,输出层的计算不能过度依赖于 h 1 , … , h 5 h_1, \ldots, h_5 h1,…,h5的任何一个元素。
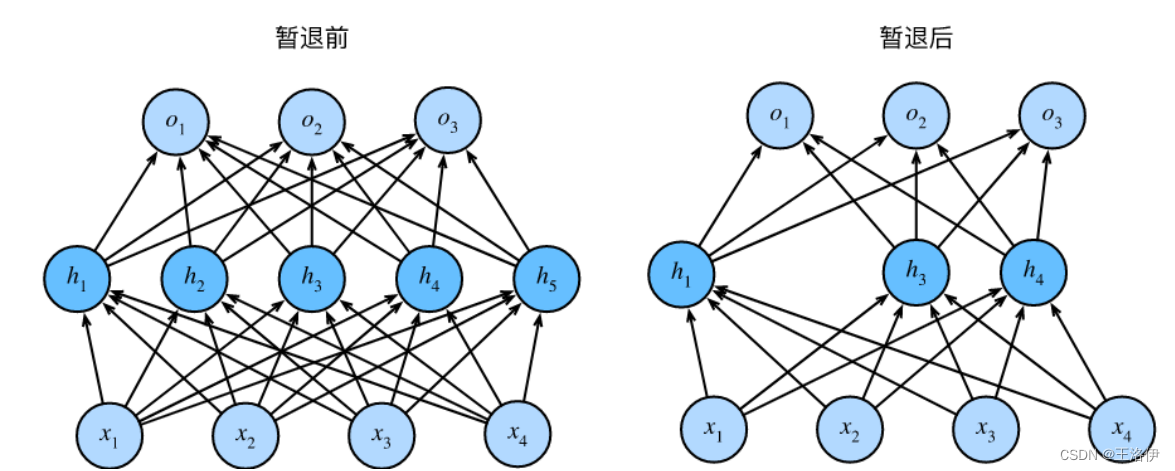
通常,我们在测试时不用暂退法。给定一个训练好的模型和一个新的样本,我们不会丢弃任何节点,因此不需要标准化。然而也有一些例外:一些研究人员在测试时使用暂退法,用于估计神经网络预测的“不确定性”:如果通过许多不同的暂退法遮盖后得到的预测结果都是一致的,那么我们可以说网络发挥更稳定。
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
# 在第一个全连接层之后添加一个dropout层
nn.Dropout(dropout1),
nn.Linear(256, 256),
nn.ReLU(),
# 在第二个全连接层之后添加一个dropout层
nn.Dropout(dropout2),
nn.Linear(256, 10))
前向传播、反向传播
前向传播
前向传播:按顺序(从输入层到输出层)计算和存储神经网络中每层的结果。
为了简单起见,我们假设输入样本是 x ∈ R d \mathbf{x}\in \mathbb{R}^d x∈Rd,并且我们的隐藏层不包括偏置项。这里的中间变量是:
z = W ( 1 ) x , \mathbf{z}= \mathbf{W}^{(1)} \mathbf{x}, z=W(1)x, 其中 W ( 1 ) ∈ R h × d \mathbf{W}^{(1)} \in \mathbb{R}^{h \times d} W(1)∈Rh×d 是隐藏层的权重参数。将中间变量 z ∈ R h \mathbf{z}\in \mathbb{R}^h z∈Rh通过激活函数 ϕ \phi ϕ后,我们得到长度为 h h h的隐藏激活向量: h = ϕ ( z ) . \mathbf{h}= \phi (\mathbf{z}). h=ϕ(z).隐藏变量 h \mathbf{h} h也是一个中间变量。
假设输出层的参数只有权重 W ( 2 ) ∈ R q × h \mathbf{W}^{(2)} \in \mathbb{R}^{q \times h} W(2)∈Rq×h,我们可以得到输出层变量,它是一个长度为 q q q的向量: o = W ( 2 ) h . \mathbf{o}= \mathbf{W}^{(2)} \mathbf{h}. o=W(2)h.
假设损失函数为 l l l,样本标签为 y y y,我们可以计算单个数据样本的损失项,
L = l ( o , y ) . L = l(\mathbf{o}, y). L=l(o,y).
根据 L 2 L_2 L2正则化的定义,给定超参数 λ \lambda λ,正则化项为
s = λ 2 ( ∥ W ( 1 ) ∥ F 2 + ∥ W ( 2 ) ∥ F 2 ) , s = \frac{\lambda}{2} \left(\|\mathbf{W}^{(1)}\|_F^2 + \|\mathbf{W}^{(2)}\|_F^2\right), s=2λ(∥W(1)∥F2+∥W(2)∥F2),
其中矩阵的Frobenius范数是将矩阵展平为向量后应用的
L
2
L_2
L2范数。
最后,模型在给定数据样本上的正则化损失为:
J = L + s . J = L + s. J=L+s.
在下面的讨论中,我们将 J J J称为目标函数(objective function)。
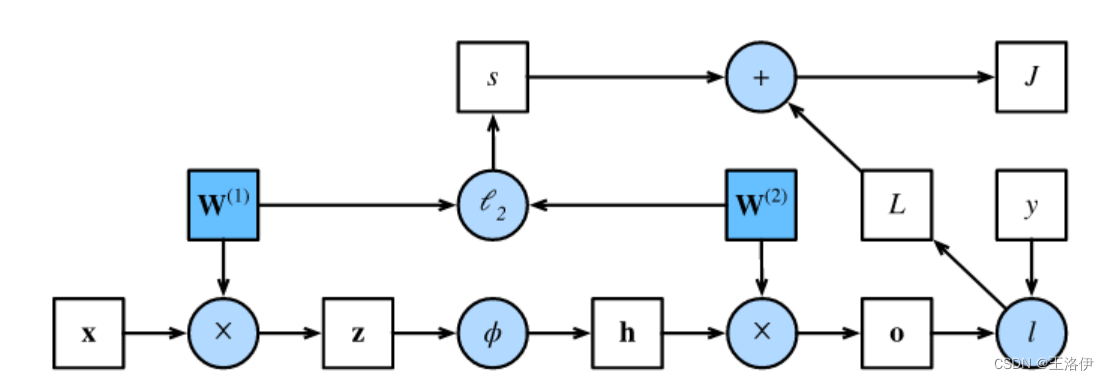
反向传播
反向传播(backward propagation或backpropagation)指的是计算神经网络参数梯度的方法。
简言之,该方法根据微积分中的链式规则,按相反的顺序从输出层到输入层遍历网络。该算法存储了计算某些参数梯度时所需的任何中间变量(偏导数)。假设我们有函数
Y
=
f
(
X
)
\mathsf{Y}=f(\mathsf{X})
Y=f(X)和
Z
=
g
(
Y
)
\mathsf{Z}=g(\mathsf{Y})
Z=g(Y),其中输入和输出
X
,
Y
,
Z
\mathsf{X}, \mathsf{Y}, \mathsf{Z}
X,Y,Z是任意形状的张量。利用链式法则,我们可以计算
Z
\mathsf{Z}
Z关于
X
\mathsf{X}
X的导数
∂ Z ∂ X = prod ( ∂ Z ∂ Y , ∂ Y ∂ X ) . \frac{\partial \mathsf{Z}}{\partial \mathsf{X}} = \text{prod}\left(\frac{\partial \mathsf{Z}}{\partial \mathsf{Y}}, \frac{\partial \mathsf{Y}}{\partial \mathsf{X}}\right). ∂X∂Z=prod(∂Y∂Z,∂X∂Y).
在这里,我们使用 prod \text{prod} prod运算符在执行必要的操作(如换位和交换输入位置)后将其参数相乘。对于向量,这很简单,它只是矩阵-矩阵乘法。对于高维张量,我们使用适当的对应项。运算符 prod \text{prod} prod指代了所有的这些符号。
单隐藏层简单网络的参数是
W
(
1
)
\mathbf{W}^{(1)}
W(1)和
W
(
2
)
\mathbf{W}^{(2)}
W(2)。反向传播的目的是计算梯度
∂
J
/
∂
W
(
1
)
\partial J/\partial \mathbf{W}^{(1)}
∂J/∂W(1)和
∂
J
/
∂
W
(
2
)
\partial J/\partial \mathbf{W}^{(2)}
∂J/∂W(2)。为此,我们应用链式法则,依次计算每个中间变量和参数的梯度。
计算的顺序与前向传播中执行的顺序相反,因为我们需要从计算图的结果开始,并朝着参数的方向努力。第一步是计算目标函数
J
=
L
+
s
J=L+s
J=L+s相对于损失项
L
L
L和正则项
s
s
s的梯度。
∂
J
∂
L
=
1
and
∂
J
∂
s
=
1.
\frac{\partial J}{\partial L} = 1 \; \text{and} \; \frac{\partial J}{\partial s} = 1.
∂L∂J=1and∂s∂J=1.
接下来,我们根据链式法则计算目标函数关于输出层变量 o \mathbf{o} o的梯度:
∂ J ∂ o = prod ( ∂ J ∂ L , ∂ L ∂ o ) = ∂ L ∂ o ∈ R q . \frac{\partial J}{\partial \mathbf{o}} = \text{prod}\left(\frac{\partial J}{\partial L}, \frac{\partial L}{\partial \mathbf{o}}\right) = \frac{\partial L}{\partial \mathbf{o}} \in \mathbb{R}^q. ∂o∂J=prod(∂L∂J,∂o∂L)=∂o∂L∈Rq.
接下来,我们计算正则化项相对于两个参数的梯度:
∂ s ∂ W ( 1 ) = λ W ( 1 ) and ∂ s ∂ W ( 2 ) = λ W ( 2 ) . \frac{\partial s}{\partial \mathbf{W}^{(1)}} = \lambda \mathbf{W}^{(1)} \; \text{and} \; \frac{\partial s}{\partial \mathbf{W}^{(2)}} = \lambda \mathbf{W}^{(2)}. ∂W(1)∂s=λW(1)and∂W(2)∂s=λW(2).
现在我们可以计算最接近输出层的模型参数的梯度
∂
J
/
∂
W
(
2
)
∈
R
q
×
h
\partial J/\partial \mathbf{W}^{(2)} \in \mathbb{R}^{q \times h}
∂J/∂W(2)∈Rq×h。
使用链式法则得出:
∂ J ∂ W ( 2 ) = prod ( ∂ J ∂ o , ∂ o ∂ W ( 2 ) ) + prod ( ∂ J ∂ s , ∂ s ∂ W ( 2 ) ) = ∂ J ∂ o h ⊤ + λ W ( 2 ) . \frac{\partial J}{\partial \mathbf{W}^{(2)}}= \text{prod}\left(\frac{\partial J}{\partial \mathbf{o}}, \frac{\partial \mathbf{o}}{\partial \mathbf{W}^{(2)}}\right) + \text{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial \mathbf{W}^{(2)}}\right)= \frac{\partial J}{\partial \mathbf{o}} \mathbf{h}^\top + \lambda \mathbf{W}^{(2)}. ∂W(2)∂J=prod(∂o∂J,∂W(2)∂o)+prod(∂s∂J,∂W(2)∂s)=∂o∂Jh⊤+λW(2).
为了获得关于 W ( 1 ) \mathbf{W}^{(1)} W(1)的梯度,我们需要继续沿着输出层到隐藏层反向传播。关于隐藏层输出的梯度 ∂ J / ∂ h ∈ R h \partial J/\partial \mathbf{h} \in \mathbb{R}^h ∂J/∂h∈Rh由下式给出:
∂ J ∂ h = prod ( ∂ J ∂ o , ∂ o ∂ h ) = W ( 2 ) ⊤ ∂ J ∂ o . \frac{\partial J}{\partial \mathbf{h}} = \text{prod}\left(\frac{\partial J}{\partial \mathbf{o}}, \frac{\partial \mathbf{o}}{\partial \mathbf{h}}\right) = {\mathbf{W}^{(2)}}^\top \frac{\partial J}{\partial \mathbf{o}}. ∂h∂J=prod(∂o∂J,∂h∂o)=W(2)⊤∂o∂J.
由于激活函数
ϕ
\phi
ϕ是按元素计算的,计算中间变量
z
\mathbf{z}
z的梯度
∂
J
/
∂
z
∈
R
h
\partial J/\partial \mathbf{z} \in \mathbb{R}^h
∂J/∂z∈Rh需要使用按元素乘法运算符,我们用
⊙
\odot
⊙表示:
∂
J
∂
z
=
prod
(
∂
J
∂
h
,
∂
h
∂
z
)
=
∂
J
∂
h
⊙
ϕ
′
(
z
)
.
\frac{\partial J}{\partial \mathbf{z}} = \text{prod}\left(\frac{\partial J}{\partial \mathbf{h}}, \frac{\partial \mathbf{h}}{\partial \mathbf{z}}\right) = \frac{\partial J}{\partial \mathbf{h}} \odot \phi'\left(\mathbf{z}\right).
∂z∂J=prod(∂h∂J,∂z∂h)=∂h∂J⊙ϕ′(z).
最后,我们可以得到最接近输入层的模型参数的梯度
∂
J
/
∂
W
(
1
)
∈
R
h
×
d
\partial J/\partial \mathbf{W}^{(1)} \in \mathbb{R}^{h \times d}
∂J/∂W(1)∈Rh×d。
根据链式法则,我们得到:
∂
J
∂
W
(
1
)
=
prod
(
∂
J
∂
z
,
∂
z
∂
W
(
1
)
)
+
prod
(
∂
J
∂
s
,
∂
s
∂
W
(
1
)
)
=
∂
J
∂
z
x
⊤
+
λ
W
(
1
)
.
\frac{\partial J}{\partial \mathbf{W}^{(1)}}= \text{prod}\left(\frac{\partial J}{\partial \mathbf{z}}, \frac{\partial \mathbf{z}}{\partial \mathbf{W}^{(1)}}\right) + \text{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial \mathbf{W}^{(1)}}\right)= \frac{\partial J}{\partial \mathbf{z}} \mathbf{x}^\top + \lambda \mathbf{W}^{(1)}.
∂W(1)∂J=prod(∂z∂J,∂W(1)∂z)+prod(∂s∂J,∂W(1)∂s)=∂z∂Jx⊤+λW(1).
在训练神经网络时,前向传播和反向传播相互依赖。 对于前向传播,我们沿着依赖的方向遍历计算图并计算其路径上的所有变量。 然后将这些用于反向传播,其中计算顺序与计算图的相反。
一方面,在前向传播期间计算正则项取决于模型参数𝐖(1)和 𝐖(2)的当前值。 它们是由优化算法根据最近迭代的反向传播给出的。 另一方面,反向传播期间参数的梯度计算, 取决于由前向传播给出的隐藏变量𝐡的当前值。因此,在训练神经网络时,在初始化模型参数后, 我们交替使用前向传播和反向传播,利用反向传播给出的梯度来更新模型参数。 注意,反向传播重复利用前向传播中存储的中间值,以避免重复计算。 带来的影响之一是我们需要保留中间值,直到反向传播完成。 这也是训练比单纯的预测需要更多的内存(显存)的原因之一。 此外,这些中间值的大小与网络层的数量和批量的大小大致成正比。 因此,使用更大的批量来训练更深层次的网络更容易导致内存不足(out of memory)错误。
梯度消失或爆炸
- 根据反向传播算法和链式法则, 梯度的计算可以简化为以下公式:
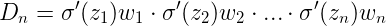
- 其中sigmoid的导数值域是固定的, 在[0, 0.25]之间, 而一旦公式中的w也小于1, 那么通过这样的公式连乘后, 最终的梯度就会变得非常非常小, 这种现象称作梯度消失. 反之, 如果我们人为的增大w的值, 使其大于1, 那么连乘够就可能造成梯度过大, 称作梯度爆炸.
- 梯度消失或爆炸的危害:
- 如果在训练过程中发生了梯度消失,权重无法被更新,最终导致训练失败; 梯度爆炸所带来的梯度过大,大幅度更新网络参数,在极端情况下,结果会溢出(NaN值).
- 梯度爆炸的解决方法
-
为了解决梯度爆炸的问题,Thomas Mikolov首先引入了一个简单的启发式解决方案,当梯度爆炸时,将梯度裁剪为一个小数值。也就是说,当它们达到某个阈值时,就会被重新设置为一个小数值
-
为了解决梯度消失问题,引入两种技术。
- 第一种技术从一个单位矩阵初始化W(hh),而不是随机初始化W(hh)。
- 第二种方法是使用校正线性单元(ReLU)代替sigmoid函数。ReLU的导数不是0就是1。通过这种方式,梯度将流经导数为1的神经元,而不会在向后传播时衰减时间步长。
-




















 367
367











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








