校验子解码问题（Syndrome Decoding）

参考文献：

1. [BMT78] E. Berlekamp, R. McEliece and H. van Tilborg, “On the inherent intractability of certain coding problems (Corresp.),” in IEEE Transactions on Information Theory, vol. 24, no. 3, pp. 384-386, May 1978, doi: 10.1109/TIT.1978.1055873.
2. [OS09] Overbeck R, Sendrier N. Code-based cryptography[M]//Post-quantum cryptography. Springer, Berlin, Heidelberg, 2009: 95-145.

校验子映射

考虑$[n,k{]}_q$线性码$\mathcal{C}$，定义余维度（codimension）$r=n-k$，令$H$是其校验矩阵。定义校验子映射（syndrome mapping）：
$$\begin{array}{rl}{S}_H:GF(q{)}^n& \to GF(q{)}^r\\ y& \mapsto y{H}^T\end{array}$$
再定义关于校验子$s\in GF(q{)}^r$的字集合：
S H − 1 ( s ) : = { y ∈ G F ( q n ) : y H T = s } S_H^{-1}(s) := \{y \in GF(q^n): yH^T=s\} SH−1​(s):={y∈GF(qn):yHT=s}
易知，$S_H^{-1}(0)=\mathcal{C}$，定义码的陪集（coset）：
y + C : = { y + x : x ∈ C } = S H − 1 ( s ← y H T ) y+\mathscr C := \{y+x: x\in\mathscr C\} = S_H^{-1}(s \leftarrow yH^T) y+C:={y+x:x∈C}=SH−1​(s←yHT)
一共存在$2^r$个陪集，每个陪集都恰好包含$2^k$个元素。

任给一个校验子，存在有效算法计算对应的陪集，

1. 将校验矩阵$H$化为系统型$H_0=UH=[I_r|X]\in GF(q{)}^{r\times n}$，这里的$U$就是$H$前$r$列的逆 U = H { 1 , ⋯   , r } − 1 U=H_{\{1,\cdots,r\}}^{-1} U=H{1,⋯,r}−1​
2. 构造$y=[s{U}^T|0]\in GF(q{)}^n$，易知$y{H}^T=y(U^{-1}{H}_0{)}^T=[s{U}^T|0][I_r|X{]}^T{U}^{-T}=s$

上述算法的复杂度是$O(r^3)$，多项式级别。

解码问题

不失一般性的，令$q=2$。

Decoding problem：令线性码$\mathcal{C}$的校验矩阵为$H$，给定一个字$y\in GF(q{)}^n$以及对应的校验子$s\in GF(q{)}^r$，下面是三种等价描述，

• 寻找一个码字$x\in \mathcal{C}$使得它拥有与$y$的最小汉明距离。
• 寻找一个错误$e\in S_H^{-1}(s)$使得它拥有最小的汉明重量。
• 寻找一个错误$e\in y+\mathcal{C}$使得它拥有最小的汉明重量。

然而，我们很难验证一个错误$e$是否真的是陪集$y+\mathcal{C}$里有最小汉明重量的那个元素。因此上述问题不属于$NP$（多项式时间可验证），我们做适当修改。

Computational Syndrome Decoding：令线性码$\mathcal{C}$的校验矩阵为$H$，给定校验子$s\in GF(q{)}^r$以及正整数$w>0$，寻找一个错误$e\in S_H^{-1}(s)$使得它的汉明重量小于等于$w$，记做$CSD(H,w,s)$。

仅当$w$使得上述问题高概率有单个解时，上述问题才有意义。可以选取$w=\lceil 1.05\cdot d_{GV}(n,r)\rceil$，这里的$d_{GV}$是 Gilbert-Varshamov distance，它被定义为使得下述不等式成立的最大正整数：
$$\sum _{i=0}^{d_0-1}\left(\genfrac{}{}{0ex}{}{n}{i}\right)\le 2^r$$
大多数二元线性码的最小距离$d_{min}$都接近其GV距离$d_{GV}$。

Codeword Finding：令线性码$\mathcal{C}$的校验矩阵为$H$，给定正整数$w>0$，寻找一个非零的码字$0\ne c\in S_H^{-1}(0)$使得它的汉明重量小于等于$w$，记做$CF(H,w)$。

令${\mathcal{C}}^{\prime }=\mathcal{C}\cup (y+\mathcal{C})$，其校验矩阵为$H^{\prime }$。很明显$CSD(H,w,y{H}^T)$的解$e$就是$CF(H^{\prime },w)$的解，因为$e\in y+\mathcal{C}\subseteq {\mathcal{C}}^{\prime }$。反之$CF(H^{\prime },w)$的解$e$，当$wt(e)<d_0$时，几乎就是$e<d_{min}(\mathcal{C})$，因此很可能$e\in y+\mathcal{C}$，从而它是$CSD(H,w,y{H}^T)$的解；而当$wt(e)\ge d_0$时，$CF(H^{\prime },w)$的一个随机解可能落在$\mathcal{C}$里也可能落在$y+\mathcal{C}$里，由于高维度随机码的测度性质与相同基数的随机集合不可区分，于是它有$1/2$的概率是$CSD(H,w,y{H}^T)$的解。

Complete Decoding：令线性码$\mathcal{C}$的校验矩阵为$H$，给定校验子$s\in GF(q{)}^r$，寻找一个错误$e\in S_H^{-1}(s)$使得它的汉明重量小于等于$d_{GV}(n,r)$。

这个问题是最一般、同时也是最困难的计算型解码问题。

另外还有相应的决策版本解码问题（decisional syndrome decoding）。敌手可以通过访问线性次决策版本的预言机，便可以求解任意的$CSD$实例，因此计算型和决策型之间没有“gap”。有文章证明，决策型解码问题属于$NPC$。于是计算型解码问题在最坏情况下是$NP-hard$的。

人们不认为存在关于$NPC$类问题的量子算法，同时针对$NP$类问题的量子算法也很难构造。

构造密码学部件

令可逆映射${\varphi }_{n,w}:GF(q{)}^l\to GF(q{)}^n$定义为
$${\varphi }_{n,w}(x)=es.t.wt(e)=w$$

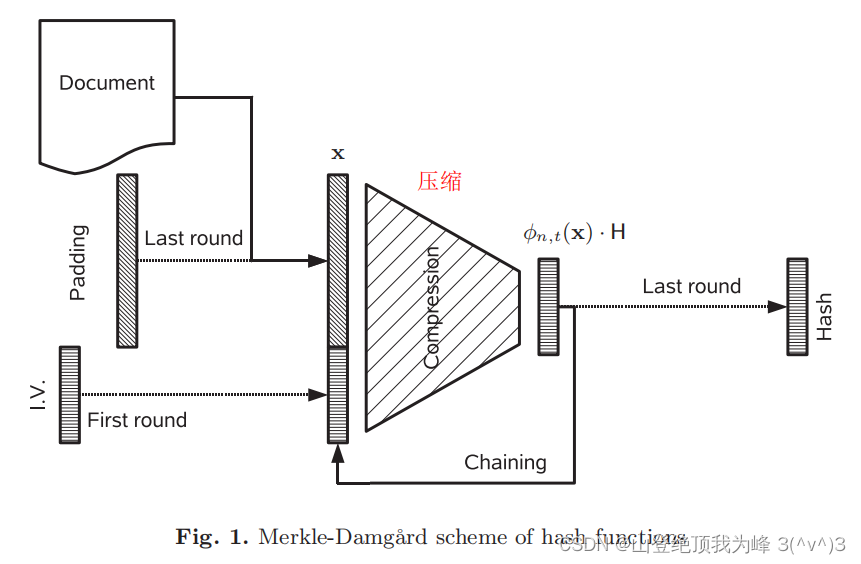
Hash

对于$[n,k]$线性码，如果选择合适的$w$满足如下关系：
$$\left(\genfrac{}{}{0ex}{}{n}{w}\right)(q-1{)}^{w-1}\ge q^{n-k}$$
那么重量为$w$的向量个数比线性码的校验子要多。如果针对校验子$s$难以恢复重量为$w$的向量（抗第二原像），那么计算校验子的过程可以作为一个压缩函数：$x\mapsto {\varphi }_{n,w}(x)H^T$

PRG

对于$[n,k]$线性码，如果选择合适的$w$满足如下关系：
$$\left(\genfrac{}{}{0ex}{}{n}{w}\right)(q-1{)}^{w-1}\le q^{n-k}$$
那么重量为$w$的向量个数比线性码的校验子要少。如果针对校验子$s$依然难以恢复重量为$w$的向量（OWP），那么计算校验子的过程可以作为一个扩展函数：$x\mapsto {\varphi }_{n,w}(x)H^T$